Waiting time probabilities in the M/G/1 + M queue - Statistics ...

WAITING TIME PROBABILITIES 11
Exp(1.5)
Erlang(2, 1.5)
Relative bias
−0.3 −0.1 0.1 0.2 0.3
R(x)=Exp(2)
R(x)=Exp(4)
Relative bias
−0.3 −0.1 0.1 0.2 0.3
R(x)=Exp(2)
R(x)=Exp(4)
0 1 2 3 4 5
0 1 2 3 4 5
Time
Time
0.75Exp(2) + 0.25Exp(4)
Lognormal(0.4, 0.3)
Relative bias
−0.3 −0.1 0.1 0.2 0.3
R(x)=Exp(2)
R(x)=Exp(4)
Relative bias
−0.3 −0.1 0.1 0.2 0.3
R(x)=Exp(2)
R(x)=Exp(4)
0 1 2 3 4 5
0 1 2 3 4 5
Time
Time
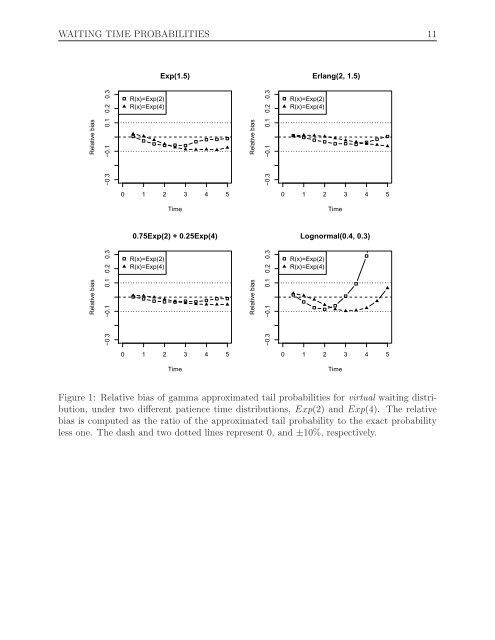
Figure 1: Relative bias of gamma approximated tail probabilities for virtual waiting distribution,
under two different patience time distributions, Exp(2) and Exp(4). The relative
bias is computed as the ratio of the approximated tail probability to the exact probability
less one. The dash and two dotted lines represent 0, and ±10%, respectively.