ST3239: Survey Methodology - The Department of Statistics and ...

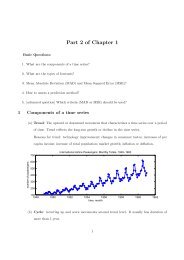
2.3 Selecting the sample size for estimating population
means
population mean
( )
We have seen that V ar(ȳ) = σ2 N−n
n N−1 . So the bigger the sample size n is (but ≤ N), the more
accurate our estimate ȳ is. It is of interest to find out the minimum n such that our estimate
is within an error bound with certain probability 1 − α, say,
i.e.,
By the central limit theorem,
P (|ȳ − µ| < B) ≈ 1 − α,
⎛
|ȳ − µ|
P ⎝ √
V ar(ȳ) <
⎞
B
√ ⎠ ≈ 1 − α.
V ar(ȳ)
B
√
V ar(ȳ) =
√
σ 2
n
B
( N−n
N−1
) ≈ z α/2 ⇐⇒
σ 2
n
( ) N − n
= B2
N − 1 zα/2
2
= D,
Thus,
⇐⇒
N
n
− 1 =
(N − 1)D
σ 2
n ≈
⇐⇒
N
n
= 1 +
(N − 1)D
σ 2
Nσ 2
B2
, where D =
(N − 1)D + σ2 zα/2
2
=
(N − 1)D + σ2
σ 2
Remark 1: if α = 5%, then z α/2 = 1.96 ≈ 2, so D ≈ B2 . This coincides with the formula in the
4
textbook (page 93).
Remark 2: the above formula requires the knowledge of the population variance σ 2 , which is
typically unknown in practice. However, we can approximate σ 2 by the following methods:
1) from pilot studies
2) from previous surveys
3) other studies.
11