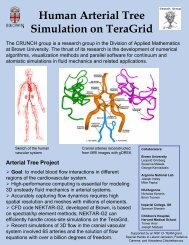
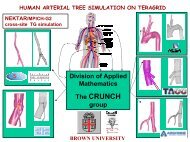
APMA2560 Homework #3 Solutions

APMA2560Homework#3Solutions
1.)ConsiderthediscreteexpansionFebruary23,2008
uN(x)=X jnjN/2u~nexp(inx); xj=2Nj;j=0;1;N?1; u~n=1 cnNXj=0 N?1u(xj)exp(?inxj);
withcn=1forjnj

gj(x).Wenowshowthatthegj(x)areLagrangefunctions.Wehave gj(xj)=1NX
=1NX jnjN/21
jnjN/21 cnein(xj?xj)
=1N0@"X jnjN/21#?11A c n
Forxlxj,wehave gj(xl)= jnjN/21 XNcnein2(l?j)/N
=1:
=?1Ncos((l?j))+e?i2(l?j)N/(2N) =?1 2Nei2(l?j)N/(2N)+e?i2(l?j)N/(2N)+1NX jnjN/2ein2(l?j)/N
N Xn=0 Nei2n(l?j)/Nn
=?1Ncos((l?j))+cos((l?j))
1?ei2(N+1)(l?j)/N
N 1?ei2(l?j)/N 1?ei2(l?j)/N
b)Inordertoderiveanexplicitformforthederivative,weuseequation(1): =0:
dxuN(xi)=24d d dxXj=0 N?1u(xj)1NX jnjN/21
=Xj=0 N?1u(xj)1NX jnjN/2in cnein(xi?xj); cnein(x?xj)35x=xi
Thuswecandeneentriesofthedierentiationmatrixas
Thatthismatrixisskew-symmetriccanbeshown: Dij=1NX
Dji=1NX jnjN/2?in cnein(xi?xj):
=?1NX jnjN/2in cne?in(xj?xi)
=?Dij: cnein(xi?xj)

ForittobeToeplitz,wehave,foralli;j

NNwithNeven,thenthefactthatDhasonezeroeigenvalueimpliesthatithasat forn0.Actually,sincewe'veshownthatDisaskew-symmetricmatrix,andsinceitis leasttwozeroeigenvalues.(Ormoregenerally,thatishasanevennumberofzeroeigenvalues.)
2.)Considerthefollowingapproximationtotheintegral
a)Ifwedenethespaceoftrigonometricfunctions 2Z02u(x)dx'1 1 N+1Xj=0 Nu(xj); xj=2j N+1;j=0;1;N:
b)Conrmtheanalyticresultbycomputationsbychoosingu(x)toillustratetheaccuracy provethattheapproximationisexactforallu(x)2B2N. BN=spanfexp(inx)gjnjN/2;
Solution: andfailureoftheapproximation.
a)Itissucienttoshowthat1 foralljnjN.Forn=0: N+1Xj=0 Neinxj=1 2Z02einxdx=n;0;
Forn0,jnjN:1 N+1Xj=0 1 Nei0xj=1
N+1Xj=0 Neinxj= N+1Xj=0
Nei2nj/(N+1)
= N+1 1 1?ei2n(N+1)/(N+1) 1?ei2n/(N+1) !
foreverynexceptn=j(N+1),j2Znf0g.Theresultsfrompartbconrmthis. Notethattheaboveresultalsoshowsthatthisquadratureruleintegrateseinxcorrectly =0
b)Weillustratetheexpectedaccuracyinthisproblem.Firstwedene
and IN(f)=1 I(f)=1 2Z02f(x)dx;
N+1Xj=0 Nf(xj);

10 0 Error in Fourier quadrature with N = 44
∣ ∣I
44(e inx ) - I(e inx ) ∣ ∣
10 −5
10 −10
astheexactintegralandapproximatequadrature,respectively.Wetake,fornoparticularlygoodreason,N=44andplottheabsoluteerrorbetweenI(f)andI44(f)ingure
quadraturetofailforn=45;90;135;:(Andinparticular,weexpectthequadraturetobeexactforalljnj44.)Inthegure,weseethisbehaviorforthepositiven.
Theerrorspikesatn=45;90;135;:Bylinearity,wecanthenconcludethatI44(f)= 1.WetakefunctionstobeFourierbasisfunctionseinx.Notethatweonlyexpectthe
haveto:foranyn0: I(f)foreveryf2B88(accuratetomachineprecision). Ofcourse,wehavenottakenintoaccountnnegative,butweclaimthatwedon't Ie?ijnjx?INe?ijnjx =0?1 =0?INe?ijnjx N+1Xj=0 Ne?ijnjx (jjisinvariantundercomplexconjugation)=0?1 N+1Xj=0 Ne+ijnjx
Therefore,weneedonlyexploretheerrorforpositiven. =Ieijnjx?INeijnjx:
Figure1.Errorinthequadratureruleforan(N+1)-pointFourierquadraturerule.TheintegratedfunctionsarethebasisfunctionsfortheFourierspace,einx.WetakeN=44here.
10 −15
0 50 100 150 200 250 300 350 400
n

3.)Considerthefollowingfunction
Weshallexplorewaysofcomputingthederivativesofu(x)usingthecontinuousanddiscrete u(x)= 5?4cos(x);x2[0;2]: 3
expansioncoecientsaswellasthedierentiationmatrix. (b)Usingtheexactcontinuousexpansioncoecients (a)Computetheanalyticderivativesofu(x)ofupto4thorder,i.e.u(m);m=1;2;3;4.
computethemaxerrorofuN(m)form=1,2,3,4andforN=2p;p=2?10:Tabulatetheresultsand discusswhatyousee. u^n=2?jnj;
discussedabove.ComputethemaxerrorofuN(m)form=1,2,3,4andforN=2p;p=2?10.Tabulatetheresultsanddiscusswhatyousee,inparticularinrelationtotheresultsintheprevious
(c)Nowrepeatthisexercisebutusethediscreteexpansioncoecientsfortheevenexpansion questions.
andtheirsources,ifyouobserveanysubstantialdierences. forN=2p;p=2?10andcomparewiththeresultsinthetwopreviouscases. (e)Discussanysubstantialdierencesbetweenthe3casesandtrytoexplainthedierences (d)Finally,usethedierentiationmatrixDderivedabovetocomputeuN(m)form=1;2;3;4
Solution: a)Thederivativesare
u(2)(x)=12(?6+5cos(x)+2cos(2x)) u(1)(x)=? (5?4cos(x))2 12sin(x)
u(3)(x)=12[?63+80cos(x)+8cos(2x)]sin(x) (5?4cos(x))3
u(4)(x)=12(670?815cos(x)?58cos(2x)+220cos(3x)+8cos(4x)) (5?4cos(x))4
b)Usingu^n=2?jnjwehave (5?4cos(x))5
uN(m)(x)=X
cision.Notethatthelimitofprecisionincreasesform;thiscorrespondstothelossofaccuracy Fromthisweobservespectralconvergenceoftheerroruntilp=7,atwhichwehitmachinepre-
jnjN/2(in)m2?jnjexp(inx)
incurredbythe(in)mmultiplication. 2p5.2000e-019.0000e+002.3632e+002.9100e+02
u(1) u(2) u(3) u(4)

3456 0.4381e+004.7500e+001.1934e+012.3875e+02
7 4.7731e-027.9688e-015.2155e+008.9671e+01
8 3.6038e-049.9487e-031.1427e-013.3366e+00
9 1.0444e-085.3924e-071.1932e-056.2914e-04
100.3997e-140.1599e-130.6395e-130.1904e-11 0.1998e-140.8882e-140.4974e-130.1604e-11 0.2665e-140.8882e-140.6395e-130.1904e-11 0.3997e-140.1421e-130.6395e-130.1904e-11
Error using continuous coefficients
10 5 N
10 0
u (1)
u (2)
u (3)
u (4)
L ∞
−error
10 −5
10 −10
c)Oncewesolveforthediscretecoecientsu~nwemayevaluatethedesiredderivativesas uN(m)(x)=X
10 −15
jnjN/2(in)mu~nexp(inx)
0 200 400 600 800 1000 1200
canseethattheerrorforthediscretecoecientsishigherthanthatofthecontinuouscoecients.Thisisaresultofthealiasingerrorintroducedbyusingthediscretecoecients.The
erroralsobeginstoincreaseafterreachingitslowestpoint(againcorrespondingtop=7).This Againwenoteaspectralconvergenceinerror,althoughcomparingtheresultsfrom(b)one
usingthe(inexact)discretecoecientsu~n. isknownasniteprecisioneectsandiscausedbytheamplicationofround-oerrorwhen
234p 0.8533e+008.5333e+002.6965e+002.9013e+02 0.6538e+004.0157e+001.3431e+012.3291e+02 0.8141e-010.5000e+006.1779e+007.7001e+01 u(1) u(2) u(3) u(4)
5678 0.6482e-030.3906e-020.1726e+002.1016e+00
9 0.1982e-070.1192e-060.2046e-040.2472e-03
100.1860e-090.8976e-070.3313e-040.1534e-01 0.2736e-110.1209e-090.7106e-080.3747e-06 0.7855e-100.8399e-090.7324e-070.9758e-05 0.4445e-100.1566e-070.2283e-050.8005e-03

Error using discrete coefficients
10 5 N
10 0
u (1)
u (2)
u (3)
u (4)
L ∞
−error
10 −5
10 −10
Tobetterillustratetheniteprecisioneects,wecanexaminethenumericalrepresentation
10 −15
0 200 400 600 800 1000 1200
areonlyabletoberesolveduptomachinezero. thatthecontinuouscoecientsareabletobeexactlyrepresentedwhereasthethediscreteones ofthediscretecoecientsu~nandcontinuouscoecientsu^n=2?jnj.Asseenbelow,wenote
coefficients for p=8 case
discrete coefficients
continuous coefficients
10 −10
c n
10 −20
10 −30
10 0
d)HereweusethedierentiationmatrixDfromquestion(1b),taking
10 −40
−150 −100 −50
uN(m)=DmuN
0 50 100 150
n
whereuNisthearrayfu(xj)g;j=0;:;N?1

derivativesfor(c)and(d)havethesameerror. reasonsas(c).Onenotesthatuptothep=7thresholdofmachineprecision,the1stand3rd Theresultsareverysimilartothosefoundinpart(c),anddierwithpart(b)forthesame
32p 0.6538e+006.0235e+001.3431e+012.6504e+02 0.8533e+001.0667e+012.6965e+002.9867e+02 u(1) u(2) u(3) u(4)
4567 0.8141e-011.0000e+006.1779e+001.0900e+02 0.6482e-030.1172e-010.1726e+004.1016e+00
98 0.1982e-070.5960e-060.2046e-040.7355e-03
10 0.6029e-100.3920e-070.1034e-040.7024e-02 0.8860e-120.4260e-100.2283e-080.1270e-06 0.1923e-100.7623e-080.1124e-050.3878e-03 0.3529e-110.2727e-090.3401e-070.2783e-05
Error using differentiation matrices
10 5 N
10 0
u (1)
u (2)
u (3)
u (4)
L ∞
−error
10 −5
10 −10
inpart(d)wearetakingthederivativeoftheinterpolant.Forexample,thesecondderivative in(c)iscomputedwiththeoperator e)Themethodusedinpart(c)correspondstotakingtheinterpolantofaderivativewhereas
10 −15
0 200 400
D(2)=INd dx2
600 800 1000 1200
whereastheoperatorusedin(d)isthematrix-matrixproduct
Itturnsoutthatfortheevenexpansion(i.e.thenumberofgridpointsiseven),theseoperators D2=INd2
arenotequal,i.e. dx2IN;
Ingeneral,foroddmtheseoperatorsarethesamewhiletheydierslightlyforevenm.Thisis observedbelow,numerically,byevaluatingthemaximumdierencebetweenthetwomethods. D(2)D2:

max difference between derivatives computed in (c) and (d)
10 5 N
10 0
u (1)
u (2)
u (3)
u (4)
10 −5
10 −10
10 −15
whiletheresultsform=2andm=4conrmthelackofcommutivityoftheoperators.
10 −20
observesthesuperioraccuracyofthecontinuousexpansionwhichisaresultofthealiasingerror Asanalcomparison,belowareplotsoftheerrorvspforthethreecases.Oneagain Again,thegrowthobservedinthem=1andm=3caseareduesolelytoroundoerrors
0 50 100 150 200 250 300
andniteprecisioneectsintroducedintheinterpolation.
10 0 u (1)
10 20 u (2)
L ∞
−error
10 −10
10 −20
b
c
d
2 4 6 8 10
p
u (3)
10 20
L ∞
−error
10 0
10 −20
2 4 6 8 10
p
u (4)
10 20
L ∞
−error
10 0
L ∞
−error
10 0
10 −20
2 4 6 8 10
p
10 −20
2 4 6 8 10
p