Handout for this lecture - Cobalt

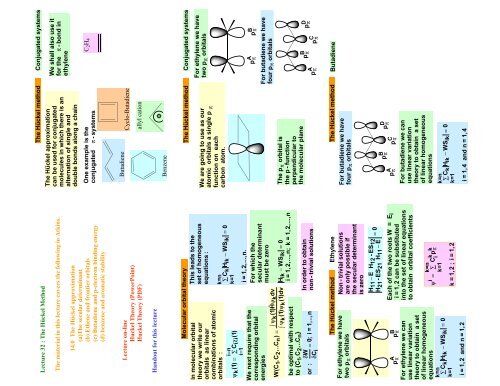
Lecture 32 : The Hückel Method
The material in this lecture covers the following in Atkins.
14.0 The Hückel approximation
(a)The secular determinant
(b) Ethene and frontier orbitals
(c) Butadiene and p-electron binding energy
(d) benzene and aromatic stability
The Hückel method
The Hückel approximation
can be used for conjugated
molecules in which there is an
alternation of single and
double bonds along a chain
One example is the
conjugated π - systems
Conjugated systems
We shall also use it
for the π - bond in
ethylene
C 2 H 4
Lecture on-line
Huckel Theory (PowerPoint)
Huckel Theory (PDF)
Handout for this lecture
Butadiene
Benzene
Cyclo-Butadiene
allyl cation
Molecular orbital theory
In molecular orbital
theory we write our
orbitals as linear
combinations of atomic
orbitals :
i=
n
ψk() 1 = ∑ Ciχi()
1
i=
1
We next require that the
corresponding orbital
energies
H dv
W C C k()ˆ
1
(C k
1 , 2,.. n)
= ∫ ψ ψ
∫ ψk() 1ψk()
1dv
be optimal with respect
to {C 1 , C 2 ,.. C n }
δ
or : W = 0; i = 1,..,n
δCi
This leads to the
set of homogeneous
equations :
k=n
∑ CkHik − WS ik = 0
k=1
i = 1,2,...,n.
For which the
secular determinant
must be zero
Hik − WSik
= 0
i = 1,2,...,n; k = 1,2,...,n
In order to obtain
non - trivial solutions
The Hückel method
We are going to use as our
atomic orbitals a single p π
function on each
carbon atom.
The p π orbital is
the p - function
perpendicular to
the molecular plane
For ethylene we have
two p orbitals π
p A π p B π
For butadiene we have
four p π orbitals
p A π
Conjugated systems
p B π
p C π
p D π
The Hückel method Ethylene The Hückel method
For ethylene we have Non - trivial solutions
For butadiene we have
two p π orbitals
are only possible if
four p π orbitals
the secular determinant
is zero
H11 − E H12 - ES12
= 0
H21 - ES 21 H11
− E
Each of the two roots W = Ei
p A p B π
π p C p D π
i = 1,2 can be substituted
π
into the set of linear equations
to obtain orbital coefficients
p A π p B π
For ethylene we can
use linear variation
theory to obtain a set
of linear homogeneous
equations
k=n
∑ CkHik − WS ik = 0
k=1
i = 1,2 and n = 1,2
k=n
ψ
i
= ∑ C
i k p
k π
k=1
k = 1,2 ; i = 1,2
For butadiene we can
use linear variation
theory to obtain a set
of linear homogeneous
equations
k=n
∑ CkHik − WS ik = 0
k=1
i = 1,4 and n = 1,4
Butadiene

The Hückel method
Butadiene The Hückel method
Non - trivial solutions
are only possible if
the secular determinant
is zero
H11 − E H12 - ES12 H13 - ES 13 H14 - ES14
H21 - ES 21 H22 − E H23 - ES 23 H24 - ES24
H31 - ES 31 H32 - ES 32 H33 − E H34 - ES34
H41 - ES 41 H42 - ES 42 H43 - ES 43 H44
− E
Each of the two roots W = Ei
i = 1,4 can be substituted
into the set of linear equations
to obtain orbital coefficients
= 0
k=n
ψ
i
= ∑ C
i k p
k π
k=1
k = 1,4 ; i = 1,4
The Hückel approximation
1. all overlaps are set to zero S ij = 0
H11 − E H12 - ES12
= 0
H21 - ES 21 H11
− E
H11 − E H12
= 0
H 21 H11
− E
H11 − E H12 - ES12 H13 - ES 13 H14 - ES14
H21 - ES 21 H22 − E H23 - ES 23 H24 - ES24
H31 - ES 31 H32 - ES 32 H33 − E H34 - ES34
H41 - ES 41 H42 - ES 42 H43 - ES 43 H44
− E
H11 − E H 12 H 13 H14
H 21 H22 − E H 23 H24
H 31 H 32 H33 − E H34
H 41 H 42 H 43 H44
= 0
= 0
The Hückel method
The Hückel approximation
1. All overlaps are set to zero S ij = 0
2. All diagonal terms are set equal to
Coulomb integral α
The Hückel method
The Hückel approximation
2
1. All overlaps are set to zero S ij = 0
2. All diagonal terms are set equal to
1
3
Coulomb integral α
3. All resonance integrals between non - neighbours
are set to zero
4
H11 − E H12
= 0
H 21 H11
− E
α − E H
=
H α −
12 0
21 E
H11 − E H 12 H 13 H14
H 21 H22 − E H 23 H24
H 31 H 32 H33 − E H34
H 41 H 42 H 43 H44
α − E H 12 H 13 H14
H 21 α − E H 23 H24
H 31 H 32 α − E H34
H 41 H 42 H 43 α - E
= 0
= 0
α − E H
=
H α −
12 0
21 E
α − E H
=
H α −
12 0
21 E
α − E H 12 H 13 H14
H 21 α − E H 23 H24
= 0
H 31 H 32 α − E H34
H 41 H 42 H 43 α - E
α − E H 12 0 0
H 21 α − E H 23 0
0 H α − E H
= 0
32 34
0 0 H 43 α - E
The Hückel method
The Hückel approximation
2
1. All overlaps are set to zero S ij = 0
1
3
2. All diagonal terms are set equal to
Coulomb integral α
3. All resonance integrals between non - neighbours
are set to zero
4. All remaining resonance integrals
are set to β
α − E H
=
H α −
12 α−
E β
0
= 0
21 E β α−
E
α − E H 12 0 0
H 21 α − E H 23 0
0 H α − E H
= 0
32 34
0 0 H 43 α - E
α−
E β 0 0
β α−
E β 0
0 β α−
E β
= 0
0 0 β α- E
4
The Hückel method
The Hückel approximation
1. All overlaps are set to zero S ij = 0
2. All diagonal terms are set equal to
Coulomb integral α
3. All resonance integrals between non - neighbours
are set to zero
4. All remaining resonance integrals
are set to β
α−
E β
= 0
β α−
E
α−
E β 0 0
β α−
E β 0
0 β α−
E β
0 0 β α- E
= 0
1
2
3
4

α β α β ψ π π
The Hückel method
Solutions for ethylene
α−
E β
= ( α−E) 2 − β
2
= 0
β α−
E
( α− E)
2
= β
2
;( α− E) = ± β
E 1 = α+
β ( α and β negative)
E 2 = − ( and negative)
k=n
∑ CkHik − WS ik = 0
k=1
i = 1,2 and n = 1,2
k=n
ψ
i
= ∑ C
i k p
k π
k=1
k = 1,2 ; i = 1,2
1 1
ψ2
=− p
1
π + p
2
π
2 2
1 1 1 2
1 = p + p
2 2
The Hückel method
Solutions for butadiene
α−
E β 0 0
β α−
E β 0
0 β α−
E β
=
0 0 β α- E
α−
E β 0 β β 0
( α − E)
β α−
E β −β
0 α−E
β =
0 β α−
E 0 β α−
E
α−
β
( α − E) 2 E
−( α−E)
β β β
β α−
E 0 ( α − E)
−
−β 2 α E β + β
20 β
=
β α−
E 0 ( α − E)
( α−E) 4
−( α−E)
2
β
2 −( α−E)
2 β
2 −( α−E)
2 β
2 +β 4
( α−E) 4
−3( α− E)
2
β
2
+ β
4
= 0
The Hückel method
Solutions for butadiene
( α−E) 4
−3( α− E)
2
β
2
+ β
4
= 0
Dividing by β
2
:
Introducing : x = ( α -E)2
β
2
Thus
( α − E) 4
( α − E)
2
− 3 + 1=
0
β
4
β
2
E = α± 1.62 β and α±
0.62β
x 2 − 3x
+ 1=
0
x = 2.62 ; x = 0.38
The Hückel method
Solutions for butadiene
k=n
∑ CkHik − WS ik = 0
k=1
i = 1,4 and n = 1,4
k=n
ψ
i
= ∑ C
i k p
k π
k=1
k = 1,4 ; i = 1,4
The Hückel molecular orbital
energy levels of butadiene and the
top view of the corresponding
π orbitals. The four p electrons
(one supplied by each C)
occupy the two lower π orbitals.
Note that the orbitals are delocalized.
The Hückel method
Solutions for butadiene
1
2
4
0.372p 1 π − 0. 602p 2 π + 0.
602p 3 π −0.372p
4 π
3
The Hückel method Solutions for butadiene
Comparison between PIB
and Huckel treatment of
butadiene
Same nodal structure
2
4
Huckel
FMO
1
3
0. 602pp 1 π −0.372 2 π −0.372p 3 π + 0.602p
4 π
α−.62β
9h 2
E 3 =
8mL 2 ,
1
2
3
4
α+.62β
−0. 602pp 1
− 0.372
2
+ 0.372p
3
+ 0.602p
4
π π π π
α+1.62β
4 h 2
E 2 =
8mL 2 ,
1
2
3
4
h 2
E 1 =
8mL 2 ,
0.372p 1 π + 0. 602p 2 π + 0.
602p 3 π + 0.372p
4 π

The Hückel method Solutions for butadiene
The Hückel method Cyclobutadiene
Butadiene
α−
E β 0
β
We can write butadiene
β α−
E β 0
as two localized π - bonds
α−.62β
0 β α−
E β
= 0
2 3
β 0 β α- E
1 4
Or two delocalized π - bonds 4π
0.5p 1 π − 05 . p 2 π + 05 . p 3 π −0.5p
4 π
α+.62β
E Bu E Et
α+1.62β
π( ) − 2 π( )
∴ delocalization
energy
α− 2β
0.5p 1 π −05 . p 2 π − 05 . p 3 π + 0.5p
4 π
Eπ( Bu) = 2( α+ 1. 62β) + 2( α+
. 62β)
Ethylene
= 4α+
4.
48β
α−β
α α
2Eπ ( Et) = 4( α+ β)
= 4α+
4β
α+ 2β
0.5p 1 π + 05 . p 2 π −05
. p 3 π −0.5p
4 π
Delocalization energy = .48β
α+β
( −36 kJ mol -1 )
0.5p 1 π + 05 . p 2 π + 05 . p 3 π + 0.5p
4 π
The Hückel method Cyclobutadiene
1
2 3
4
1
2
4
3
No delocalization
energy
The Hückel method Benzene
The C - C and C - H
σ - orbitals
α− 2β
α−
β
α α
Benzene
α+ 2β
α+
β
The framework of benzene
is formed by the overlap of Csp2
hybrids, which fit without strain
into a hexagonal arrangement.
The Hückel method
Benzene
The Hückel method
Benzene
α−
E β 0 0 0 β
β α−
E β
0
β 0 α−
E β 0 0
0 0 β α−
E β 0
0 0 0 β α- E β
β 0 0 β β α- E
= 0
α− 2β
α−
β
Delocalization energy =
2( α+ 2 β) + 4( α+ β) − 6( α+
β)
= 2β
−150 kJ mol -1
E= α± 2 β ; α± β;
α±
β
α+
β
k=n
k=n
∑ CkHik − WS ik = 0 ψ
i
= ∑ C
i k p
k π
k=1
k=1
α+ 2β
i = 1, 6 and n = 1, 6
k = 1, 6 ; i = 1, 6

What you should learn from this lecture
1. Be able to construct the secular
determinant for a conjugated π - system
within the Huckel approximation
2. Be able to calculate orbital
energies for simple systems
The Hückel method
allyl cation
2
3
The allyl system
α−
E β 0
β α−
E β
0 β α−
E
= 0
3. You will not be asked to find
the molecular orbitals. However,
you should be able to discuss
provided orbitals in terms of bonding
and anti - bonding interactions
α− 142 . α
α
0.5p 1 π − 0. 707p 2 π + 0.
5p
3 π
0.707p 1 π − 0.
707p
3 π
α+ 142 . α
0.5p 1 π + 0. 707p 2 π + 0.
5p
3 π