Interpolation and Curve Fitting

Interpolation and 

Curve Fitting 

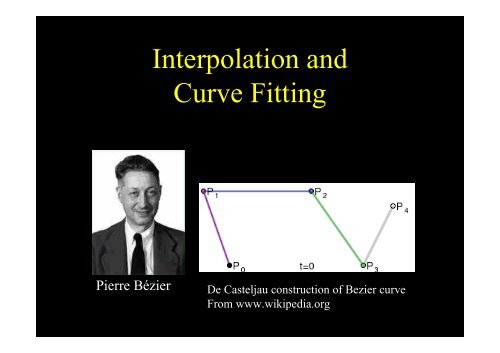
Pierre Bézier 

De Casteljau construction of Bezier curve 

From www.wikipedia.org

Bezier Curves and B-Spline Curves 

• Not really “interpolating”curves as they 

normally do not pass through data points 

• Curves stay within the polygon defined by the 

given points 

• Local control: effect of changing a knot is 

limited to a local region in Bezier and b-spline 

• Global control: moving a knot in a cubic spline 

affects the whole curve 

Numerical Methods © Wen-Chieh Lin 2

Global vs. Local Control 

• Does a small change affect the whole curve or 

just a small segment? 

• Local is usually more intuitive and provided 

by composite curves 

Global 

Local 


Parametric Form 

• Explicit function 

y f 

(x) 

• Parametric form 

x F ( u) 

1 

y F ( u) 

2 

• Example: unit circle 

x cos(u) 

y sin(u) 


Interpolation in Parametric Form 

• Given n+1 control points, 

x 

i 

pi 

 

y 

 

i 

, i 0 ,..., n 

 

 

zi 

 

• Compute interpolation functions 

x 

( u) 

 

( u) 

 

 

y( 

u) 

 

, 0 u 

1 

 

 

z( 

u) 

 

P j 

j: index for each segment of curve 


Composite Segments 

• Divide a curve into multiple segments 

• Represent each in a parametric form 

• Maintain continuity between segments 

• position 

• tangent 

• curvature 

P 1 (u) P 2 (u) P 3 (u) P n (u) 


Cubic 3D Curves 

• Three cubic polynomials, one for each coordinate 

3 2 

x( 

u) 

a 

u b 

u c 

u d 

y( 

u) 

z( 

u) 

a 

a 

• In matrix notation 

x 

y 

z 

u 

u 

3 

3 

b 

x 

y 

z 

u 

b u 

2 

2 

c 

c 

z 

x 

y 

u d 

u d 

a 

 

b 

 

c 

 

d 

3 

2 

x( 

u) 

y( 

u) 

z( 

u) 

u 

u u 1 

Numerical Methods © Wen-Chieh Lin 7 

x 

x 

x 

x 

z 

x 

y 

a 

b 

c 

c 

y 

y 

y 

y 

a 

b 

c 

d 

z 

z 

z 

z

Hermite Interpolation 

• Hermite interpolation requires 

• values at endpoints 

• derivatives at endpoints 

x( 

u) 

a 

x 

u 

3 

b 

x 

u 

c 

Needs 4 equations to 

solve 4 unknowns 

2 

x 

u 

d 

x 

• To create a composite curve, use the end of 

one as the beginning of the other and share the 

tangent vector 

P(0) 

control points/knots 

P(1) 

P '(0) 

P' (1) 


Hermite Curve Formation— 

consider x coordinate first 

• Cubic polynomial and its derivative 

3 2 

x( 

u) 

a 

u b 

u c 

u 

x' 

( u) 

• Given x i , x i+1 , x’ i , x’ i+1 , solve for a, b, c, d 

• 4 equations are given for 4 unknowns 

x 

x 

x 

2 

3 

a u 2 

b 

x 

x 

u c 

x 

d 

x(0) 

x i 

d x 

x(1) 

x 

i 1 

a 

x 

b 

x 

c 

x 

d 

x' 

(0) x' 

i 

c x 

x (1) x 

' 

3 

a 2 

b c 

' 

i 1 

x 

x 


x 

x 

x

Hermite Curve Formation (cont.) 

• Problem: solve for a, b, c, d 

x(0) 

x i 

d x 

x(1) 

x 

i 1 

a 

x 

b 

x 

c 

x 

d 

x' 

(0) x' 

i 

c x 

x (1) x 

' 

3 

a 2 

b c 

' 

i 1 

x 

x 

x 

x 

• Solution: 

a 

b 

c 

d 

x 

x 

x 

x 

2( 

x 

3( 

x 

x 

' 

x 

i 

i 

i 

i1 

x 

i1 

x 

i 

) x 

' 

i 

) 2 

x' 

x 

' 

i 

i1 

x 

' 

i1 



• The coefficients can be expressed as linear 

combination of geometric information 

a 

b 

c 

d 

x 

x 

x 

x 

2( 

x 

3( 

x 

x 

' 

x 

i 

i 

i 

i1 

x 

i1 

x 

i 

) x 

' 

i 

) 2 

x' 

a 

 

b 

 

c 

 

d 

x 

x 

x 

x 

x 

' 

i 

i1 

x 

' 

2 

 

3 

 

 

0 

 

1 

i1 

2 

3 

0 

0 

1 

2 

1 

0 

1 

xi 

1 

 

x 

 

i 

0 

x' 

 

0 

x' 

i 

1 

i 

1 

 

 

 

 

 

 



• x component of Hermite curve is then represented as 

x( 

u) 

 

3 

u 

 

u 

u 

2 

3 

u 

u 

2 

u 

2 

 

 

3 

1 

0 

 

1 

a 

 

 

b 

1 

c 

 

d 

x 

x 

x 

x 

2 

3 

0 

0 

 

 

 

 

 

 

1 

2 

1 

0 

1 

xi 

1 

 

x 

 

i 

0 

x' 

 

0 

x' 

i 

1 

i 

1 

 

 

 

 

 

 



• Including y and z components 

3 

2 

x( 

u) 

y( 

u) 

z( 

u) 

u 

u u 1 

 

3 

u 

P(u) 

u 

2 

u 

2 

 

 

3 

1 

0 

 

1 

2 

3 

0 

0 

1 

2 

1 

0 

a 

 

b 

 

c 

 

d 

x 

x 

x 

1 

xi 

1 

 

x 

 

i 

0 

x' 

 

0 

x' 

i 

u T M p 

x 

1 

i 

1 

y' 

i1 

y' 

i1 

 

 

 

 

 

 

z' 

i1 

z' 

i1 

 

 

 

 

 

 


a 

b 

c 

d 

y 

y 

y 

y 

y 

y 

a 

b 

c 

d 

i 

i 

z 

z 

z 

z 

z 

z 

i 

i

Hermite Interpolation in Matrix Form 

P(u) 

u 

u T u [ 

3 

T 

, u 

Mp 

2 

, u,1] 

2 

 

3 

M 

0 

 

1 

is 

2 

2 

the parameter 

M is the cofficient matrix 

p is the geometric information 

P(0) 

3 

0 

0 

1 

1 

0 

1 

1 

 

 

0 

 

0 

control points/knots 

P(1) 

P '(0) 

P' (1) 

p 

i 

 

p 

 

i 

p 

p 

' 

i 

 

p 

' 

i 

P 

(0) 

 

P(1) 

 

 

 

P 

'(0) 

 

 

P 

'(1) 

 


1 

1 

ith segment in 

composite curves

Blending Functions of Hermite Splines 

• Each cubic Hermite spline is a linear combination of 

4 blending functions 

P( 

u) 

u 

geometric information 

T 

Mp 

P( 

u) 

3 2 

2 

u 3 

u 1 

pi 

 

3 2 

 

2 

u 3 

u 

 

p 

 

i 

3 2 

u 2 

u u 

p' 

 

3 2 

 

u u 

 

p 

' 

i 

T 

1 

i 

1 

 

 

 

 

 

 


Bezier Curves 

• Another variant of the same game 

• Instead of endpoints and tangents, four control 

points 

• points p 0 

and p 3 

are on the curve 

• points p 1 

and p 2 

are off the curve 

• P(0) = p 0 

, P(1) = p 3 

• P’(0) = 3(p 1 

- p 0 

), P’(1) = 3(p 3 

- p 2 

) 

3 

2 

P( 

u) 

 

u 

u 

u 

1 

 

 

2 

 

2 

1 

 

 

3 

3 

 

2 

 

 

0 

0 

1 

 

 

1 

0 0 

1 

 

P 

1(0) 

00 

 

1 

 

 

P0 

(1) 00 

 

 

0 

 

 

P' 

3(0) 

3 

0 

 

 

0 

 

P 

0' 

(1) 0 

3 

p 0 

p 1 

p 2 

p 3 

0 

p 

1 

 

p 

 

0 

p 

 

3 

p 

 

 

 

 

 

 


0 

1 

2 

3

Bezier Curves (cont.) 

• Variant of the Hermite spline 

• basis matrix derived from the Hermite basis 

• Gives more uniform control knobs (series of 

points) than Hermite 

• The slope at u = 0 is the slope of the secant 

line between p 0 and p 1 

P' (0) 3( 

p 1 

p 

0) 

dx du 3 ( x 1 

x 

0) 

dy du 3 ( y 1 

y 

0) 

dy dx y y 

) ( x 

( 

1 0 1 

x 

0 

) 


Blending Functions of Bezier Curves 

• Also known as degree 3 Bernstein polynomials 

• Weighted sum of Bernstein polynomials (infinite 

series) converges uniformly to any continuous 

function on the interval [0,1] 

P( 

u) 

3 

(1 

u 

) p 

 

2 

3 

u(1 

u 

) p 

 

 

i 

2 

3u 

(1 u 

) p 

i 

 

3 

 

u 

p 

i 

T 

i 

1 

2 

3 

 

 

 

 

 

 


Composing Bezier Curves 

• Control points at consecutive segments need 

be collinear to avoid a discontinuity of slope 


Interpolation, Continuity, and 

• Hermite/Bezier splines 

• Interpolate control points 

• Local control 

Local Control 

• No C2 continuity for cubics 

• Cubic (Natural) splines 

• Interpolate control points 

• No local control - moving one control point affects whole 

curve 

• C2 continuity for cubics 

• Can’t get C2, interpolation and local control with cubics 


Cubic B-Splines 

• Basis-spline (B-spline) 

• Give up interpolation 

• the curve passes near the control points 

• best generated with interactive placement (it’s hard 

to guess where the curve will go) 

• Curve obeys the convex hull property 

• C2 continuity and local control are good 

compensation for loss of interpolation 


Cubic B-splines (cont.) 

• Any evaluation of conditions of B i (1) cannot use p i+3 , 

because p i+3 does not appear in B i (u) 

• Evaluation conditions of B i+1 (0) cannot use p i-1 

• Two conditions satisfy this symmetric condition 

pi 

4 

pi 

Bi 

1) B 

i1 

(0) 

6 

p i 

p i1 

B B 

i 

i 1 

p 

1 

i2 

( 

p 

i 

p 

i2 

B' i 

(1) B 

' 

i1 

(0) 

2 

p i1 

p i2 

B i2 

p i4 

p i3 


• From 

Solving for B-spline Coefficients 

B ( u) 

• We can obtain 

B 

B 

i 

(0) 

 

i 

d i 

(1) a 

B' 

B' 

i 

(0) 

i 

 

i 

B' 

i 

c i 

i 

b 

( u) 

i 

a u 

c 

(1) 3 

a 2 

b 

i 

i 

3 

i 

b u 

i 

2 

c u d 

2 

3 

a u 2 

b u c 

i 

i 

d 

c 

i 

i 

• We can solve a set of 4 equations for a, b, c, d 

i 

i 

i 

i 

Then plug in the followings 

pi 

4 

pi 

1 

p 

i 

Bi 

1) B 

i1 

(0) 

6 

pi 

1 

4 

pi 

p 

i1 

Bi 

( 0) 

6 

p 

i 

p 

i2 

B' i 

(1) B 

' 

i1 

(0) 

2 

p 

i1 p 

i1 

B' i 

(0) 

2 

2 

( 


Cubic B-splines in Matrix Form 

B ( u) 

i 

u 

T 

Mp 

1 

 

6 

u 

3 

u 

2 

u 

 

1 

 

 

3 

1 

 

3 

 

1 

3 

6 

0 

4 

3 

3 

3 

1 

1 

pi 

0 

 

p 

 

0 

pi 

 

0 

pi 

1 

i 

1 

2 

 

 

 

 

 

 

B B 

i 

i 1 

( u 0 

) 

p i 

p i1 

b 

) 

b 1 

( u 

p i1 

p i2 

B i2 

b 

( ) b ( u 2 

) 

1 

u 

p i4 

p i3 


Blending Functions of Cubic B-Splines 

• Represent cubic b-spline as 

B 

• Blending functions 

b 

b 

b 

3 

(1 u 

) 

6 

3 

u 2 

u 

2 

3 

u u 

 

2 2 

1 

 

0 

 

i( u) 

b 

1 

pi 

1 

b 

0 

pi 

b 

1pi1 

b 

2 

pi 

2 

2 

3 

u 

 

2 

1 

 

b 

1 

u 

 

6 

3 

1 

6 

b 0( 

u ) 

b 1 

( u) 

b 

( ) ( ) 

1 

u 

2 u 


b 

2

Continuity in Cubic B-splines 

• Continuity conditions similar to cubic spline 

B 

pi 

4 

pi 

1 

p 

i 

1) B 

i1 

(0) 

6 

p 

i 

p 

i 

(1) B 

' 

i1 

(0) 

2 

(1) B 

" (0) p 

p p 

2 

i( B 

B 

2 

' 

i 

" 

i 

i1 i 

2 

i1 

i2 

Prove that this condition 

is automatically satisfied 

if the first two hold! 

p i 

p i1 

B B 

i i 1 

p i 

1 

p i2 

B i2 

p i4 


p i3

Composing B-splines 

• Given points p 0 , …, p n , we can construct B- 

splines B 1 through B n-2 

• We need additional points outside the domain of 

the given points to construct B 0 and B n-1 

• Add fictitious points p -2 , p -1 , p n+1 , p n+2 

• Set p -2 = p -1 = p 0 and p n+2 = p n+1 = p n so that the 

curve starts and ends at the given extreme points 


Comparison of Basic Cubic Splines 

Type Control points Continuity Interpolation 

Natural n points, shared C2 Y 

Hermite 2 points, 2 slopes C1 Y 

Bezier 4 points C1 Y 

B-Splines 4 points, shared C2 N 


Interpolating on a Surface 

• Bezier surfaces 

• B-Spline surfaces 


Bicubic Surfaces 

• To represent surfaces use bicubic functions 

• x(u,v), y(u,v), z(u,v) are cubic polyomials both in u 

and v 

• 16 terms for combination of powers of u and v 

x 

3 3 3 2 

( u, 

v) 

a 

11u 

v a 

12u 

v 

a 

44 

• A bicubic surface can be represented by a 4x4 

matrix A 

x( u, 

v) 

u T Av 

• Also known as tensor surfaces 

u 

T 

 

u 

1 


3 

3 

u 

2 

u 

2 

v v v v 1 

T


Cubic B-Spline Surfaces 

• Recall B-spline curve: 

v 

M 

MX 

u 

Av 

u 

T 

j 

i 

ij 

v 

u 

x , 

T 

T 

) 

, 

( 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 

1 

1 

2 

3 

0 

1 

4 

1 

0 

3 

0 

3 

0 

3 

6 

3 

1 

3 

3 

1 

1 

6 

1 

) 

( 

i 

i 

i 

i 

T 

i 

p 

p 

p 

p 

u 

u 

u 

u 

B 

Mp 

u 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 

2, 

1 

2, 

2, 

1 

2, 

2 

1, 

1 

1, 

1, 

1 

1, 

2 

, 

1 

, 

, 

1 

, 

2 

1, 

1 

1, 

1, 

1 

1, 

j 

i 

j 

i 

j 

i 

j 

i 

j 

i 

j 

i 

j 

i 

j 

i 

j 

i 

j 

i 

j 

i 

j 

i 

j 

i 

j 

i 

j 

i 

j 

i 

ij 

x 

x 

x 

x 

x 

x 

x 

x 

x 

x 

x 

x 

x 

x 

x 

x 

X


 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 

1 

1 

2 

3 

0 

0 

0 

1 

0 

0 

3 

3 

0 

3 

6 

3 

1 

3 

3 

1 

1 

) 

( 

i 

i 

i 

i 

T 

i 

p 

p 

p 

p 

u 

u 

u 

u 

Mp 

u 

P 

Bezier Surfaces 

• Recall Bezier curve: 

v 

M 

MX 

u 

Av 

u 

T 

j 

i 

ij 

v 

u 

x , 

T 

T 

) 

, 

( 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 

2, 

1 

2, 

2, 

1 

2, 

2 

1, 

1 

1, 

1, 

1 

1, 

2 

, 

1 

, 

, 

1 

, 

2 

1, 

1 

1, 

1, 

1 

1, 

j 

i 

j 

i 

j 

i 

j 

i 

j 

i 

j 

i 

j 

i 

j 

i 

j 

i 

j 

i 

j 

i 

j 

i 

j 

i 

j 

i 

j 

i 

j 

i 

ij 

x 

x 

x 

x 

x 

x 

x 

x 

x 

x 

x 

x 

x 

x 

x 

x 

X

Bezier Surfaces 

p ( 0,0) p 

0,0) 3( 

p 10 

p 

) 

00 

p 

u 

p 

v 

( 

00 

( 0,0) 3( 

p 01 

p 

00) 

u 

v 


Least Square Approximation 

• Measurement errors are inevitable in 

observational and experimental sciences 

• Errors can be smoothed out by averaging over 

many cases, i.e., taking more measurements 

than are strictly necessary to determine 

parameters of system 

• Resulting system is overdetermined, so usually 

there is no exact solution 


Least Square Approximation 

• Higher dimensional data are projected into 

lower dimensional space to suppress irrelevant 

details 

• Such projection is most conveniently 

accomplished by least square method 

Linear projection from 2D to 1D space: 

Original data distributed in a 2D space 

They can be approximated as a 1D line 


Linear Least Squares 

• For linear problems, we obtain overdetermined 

linear system Aa = b with m×n matrix A, m > n 

• System is better written Aa ≈b, since equality 

is usually not exactly satisfied when m > n 

• Least squares solution a minimizes squared 

Euclidean norm of residual vector r = b - Aa 

min 

a 

r 

2 

min 

2 

a 

b 

Aa 

2 

2 


Curve Fitting 

• Given m data points (x i , y i ), find n-vector a of 

parameters that gives “best fit”to model 

function y = f(x, a), m 

2 

min ( y f 

( x, 

a)) 

 

• Problem is linear if function f is linear in 

components of a 

f ( x, 

a) 

a 

( 

x) 

a 

( 

x) 

 

a 

n( 

x) 

1 1 2 2 

n 

Aa≈b with A ij =φ j (x i ) and b i =y i 

i1 

• Problem can be written in matrix form as 

a 

i 


• Polynomial fitting 

f 

Curve Fitting (cont.) 

( x, 

a) 

a 

is linear, since polynomial linear in coefficients, 

though nonlinear in independent variable x 

• Fitting sum of exponentials 

is example of nonlinear problem 

• We will only consider linear least squares 

problems for now 

1 

a 

2 

x 

 

 

n 

a n 

x 

f ( x, 

a) 

a e 

a2x 

 

a 

1 

n1 

1 


e 

a 

n 

x

Example: curve fitting 

• Fitting quadratic polynomial to five data points 

gives linear least squares problem 

Aa 

1 

 

 

1 

 

1 

 

1 

 

1 

x 

x 

x 

x 

x 

1 

2 

3 

4 

5 

x 

x 

x 

x 

x 

2 

1 

2 

2 

2 

3 

2 

4 

2 

5 

 

 

 

a 

 

a 

 

 

a 

 

 

1 

2 

3 

y 

 

y 

 

 

 

y 

 

 

 

 

y 

 

y 

1 

2 

3 

4 

5 

 

 

 

 

 

 

 


Example: curve fitting (cont.) 

• For data x -1.0 -0.5 0.0 0.5 1.0 

y 1.0 0.5 0.0 0.5 2.0 

overdetermined linear system is 

1 

 

1 

 

Aa 

1 

 

 

1 

 

1 

1.0 

0.5 

0.0 

0.5 

1.0 

1.0 

0.25 

 

a 

 

0.0 

 

a 

 

 

0.25 

 

 

a 

1.0 

1.0 

 

 

0.5 

 

 

 

0.0 

 

 

 

 

0.5 

 

 

2.0 

• Solution, which we will see later how to compute, 

is 

T 

a [0.086 0.40 1.4] 

1 

2 

3 


Example (cont.) 

• The computed approximation polynomial is 

p( x) 

0.086 

0.4 

x 1.4 

x 

• Resulting curve and original data points are 

shown in graph 

2 


Normal Equations 

• To minimize squared Euclidean norm of 

residual vector 

2 

T 

T 

r r 

r ( 

b Aa 

) ( b Aa 

) 

2 

T T T T T 

b 

b 2 

a A b a 

A Aa 

• Take derivative with respect to a and set it to 0 

T 

T 

2A 

Aa 2 

A b 0 

which reduces to n×n linear system of normal 

equations 

T 

T 

A Aa A 

b 


Orthogonality 

• Space spanned by columns of m × n matrix A, 

span( 

A) 

{ 

Aa : aR 

, is of dimension at most n 

• If m > n, b generally does not lie in span(A), 

so there is no exact solution to Aa = b 

• Vector y = Aa in span(A) closest to b in 2- 

norm occurs when residual r = b - Aa is 

orthogonal to span(A), 

again giving system of 

n 

} 

0 A 

T 

r 

A 

T 

(b Aa) 

A 

T 

Aa A 


T 

b

Orthogonality (cont.) 

• Geometric relationships among b, r, and 

span(A) are shown in diagram 

b 

r 

b 

Aa 

span(A) 

y Aa 


Pseudoinverse and Condition Number 

• Nonsquare m × n matrix A has no inverse in 

usual sense 

• If rank(A) = n, pseudoinverse is defined by 

T T 

A 

1 

( 

A A) 

A 

and condition number by 

cond(A) A 

• By convention, cond(A) = ∞ if rank(A) < n 

A 

 


Pseudoinverse and Condition Number 

• Just as condition number of square matrix 

measure closeness to singularity, condition 

number of rectangular matrix measures 

closeness to rank deficiency 

• Least squares solution of Aa≈b is given by 

a=A + b 


Sensitivity and Conditioning 

• Sensitivity of least squares solution to Aa≈b 

depends on b as well as A 

• Define angle θbetween b and y = Aa by 

y 

cos( ) 

 

b 

• Bound on perturbation ∆x in solution x due to 

perturbation ∆b in b is given by 

x 

x 

2 

2 

2 

2 

cond 

( A) 

Aa 

 

b 

1 

cos( 

2 

2 

) 

b 

2 


b 

2

Sensitivity and Conditioning 

• Similarly, for perturbation E in matrix A, 

x 

x 

2 

2 

cond ( A)(tan( 

cond ) ( A) 

1 

) 

E 

A 

2 

2 

• Condition number of least squares solution is 

about cond(A) if residual is small, but can be 

squared or arbitrarily worse for large residual 


Normal Equation Method 

• If m × n matrix A has rank n, then symmetric n × 

n matrix is positive definite, so its Cholesky 

factorization 

T 

T 

A A LL 

can be used to obtain solution a to system of 

normal quations T 

T 

A Aa A 

b 

which has same solution as linear least squares 

problem Aa≈b 

• Normal equations method involves 

transformations: 

rectangular square triangular 


Example: Normal Equation Method 

• For polynomial data-fitting on 

x -1.0 -0.5 0.0 0.5 1.0 

y 1.0 0.5 0.0 0.5 2.0 

• Normal equations method gives 

A T A 

1 

 

 

1.0 

 

 

1.0 

1 

0.5 

0.25 

1 

0.0 

0.0 

1 

0.5 

0.25 

1 

1 

 

1 

 

1.0 

 

1 

 

 

1.0 

 

1 

 

1 

1.0 

0.5 

0.0 

0.5 

1.0 

1.0 

0.25 

 

5.0 

 

0.0 

 

0.0 

 

 

0.25 

 

 

2.5 

1.0 

0.0 

2.5 

0.0 

2.5 

0.0 

 

 

2.125 


Example: Normal Equation Method 

• For polynomial data-fitting on 

x -1.0 -0.5 0.0 0.5 1.0 

y 1.0 0.5 0.0 0.5 2.0 

• Normal equations method gives 

1 

A T b 

 

1.0 

 

 

1.0 

1 

0.5 

0.25 

1 

0.0 

0.0 

1 

0.5 

0.25 

1.0 

 

1 

 

0.5 

4.0 

 

 

1.0 

 

0.0 

 

1.0 

 

 

 

 

1.0 

 

0.5 

 

 

3.25 

 

2.0 


Example (cont.) 

• Choleskey factorization of symmetric positive 

definite matrix A T A gives 

5.0 

A T A 

 

0.0 

 

 

2.5 

0.0 

2.5 

0.0 

2.5 2.236 

0.0 

 

 

 

0.0 

 

2.125 

 

1.118 

1.581 

0.0 

2.236 

0.0 

 

0.0 

 

0.935 

 

0.0 

1.581 

• Solving lower triangular system Lz = A T b by 

forward substitution gives z = [1.789 0.632 1.336] T 

• Solving lower triangular system La = z by forward 

substitution gives a = [0.086 0.400 1.429] T 

0.0 

0.0 

0.0 

0.0 

1.118 

0.0 

0.935

Interpolation and Curve Fitting

Create successful ePaper yourself

Delete template?

Save as template?