Meshfree and particle methods and their applications - TAM ...

10 Li and Liu: Meshfree and particle methods and applications Appl Mech Rev vol 55, no 1, January 2002
where I n1 (x) is the n1 order moving least square interpolant.
In general, L i (x) may be regarded as the Taylor expansion
of u(x) at point x I . The reason using Legendre
polynomial as p-enrichment is its better conditioning; a similar
procedure is well established in p-version finite element
219. An early paper by Liu et al 188 proposed an interpolation
formula that is aslo similar to Eq. 45; it is called
the multiple-scale spectral finite element method. The Legendre
polynomial enrichment basis is called by Belytschko
et al 60 as extrinsic basis, and it is attached to the intrinsic
basis, I n1 (x) to form a p-cloud. There is a seldom mentioned
belief among the advocates of h-p clouds. That is one
can build h-p clouds on the simplest meshless partition of
unity—the Shepard interpolant, ie, one can pile up higher
order polynomial to Shepard interpolant. By so doing, one
does not need the matrix inversion when constructing higher
order meshfree shape function; one may still be able to enjoy
good interpolation convergence.
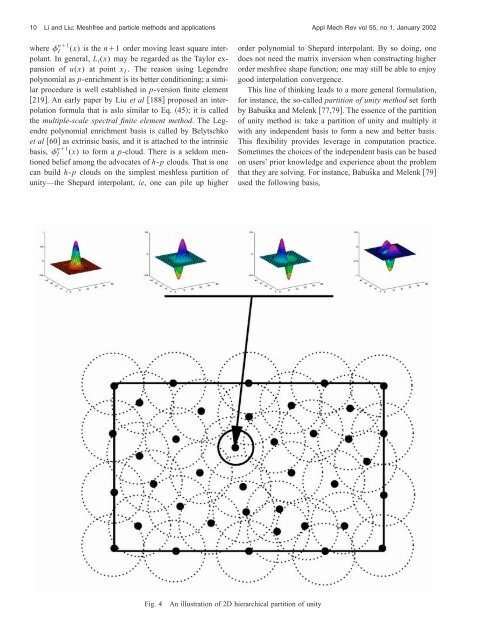
This line of thinking leads to a more general formulation,
for instance, the so-called partition of unity method set forth
by Babuška and Melenk 77,79. The essence of the partition
of unity method is: take a partition of unity and multiply it
with any independent basis to form a new and better basis.
This flexibility provides leverage in computation practice.
Sometimes the choices of the independent basis can be based
on users’ prior knowledge and experience about the problem
that they are solving. For instance, Babuška and Melenk 79
used the following basis,
Fig. 4
An illustration of 2D hierarchical partition of unity