Homework Assignment #1: Answer Key

ief answer It must mean that the elasticity of substitution is at least unity. We can
substitute other inputs for declining resources without output falling. In fact, the
production function we have chosen has =1. We have assumed that resources are
notabindingconstraintongrowth. Butif1 then the share going to resource
owners would rise as resources became more scarce — in other words, would increase
as declined. So would not be a constant in (6), and thus your answer to part d
understates the effect of declining resources in the case where substitution is difficult.
We know from problem 1 that if production was Leontief then the share of national
income that would go to resource owners would increase dramatically as → 0
As your analysis in problem 1 shows, if =0then the share of income that goes
tothescarceresourcegoesto100%,so −→ 1, and the drag approaches + ,
which would overwhelm all sources of growth (it would still be true if 0 1).
This is clearly a result that is consistent with the apocalyptic intuition about resource
scarcity. When I wrote the production function as = ( ) 1−− I, in fact,
assumed that =1(with such a production function, called Cobb-Douglas, the factor
shares are independent of the capital labor ratio), as the shares and are constant.
But, in fact, we know that the share of income going to resource owners has actually
been falling in the US during the 20th century (real oil prices, for example, have
been roughly constant and energy consumption per unit of GDP has been falling).
So rather than 1 it seems almost certain that 1, and that the small drag
computed in part d is closer to the truth.
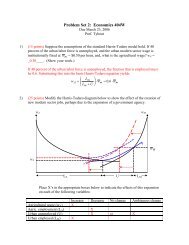
3. Consider the basic Hotelling model of exhaustible resources. Assume a competitive economy
with many producers, a fixed cost of extraction, , and a choke price, . The rate of interest
is given at rate . What happens to the extraction path of the resource (the plot of output,
,againsttime)if:
(a) the rate of interest falls.
brief answer In class we analyzed a rise in , so this case is exactly opposite. If
falls, it is all of a sudden better to keep a dollar’s worth of oil in the ground than a
dollar in the bank. So oil production falls. This causes 0 to rise and 0 to fall. The
Hotelling Rule requires that net rent grows at the rate of interest which is now lower.
So clearly the time to exhaustion must rise. If price starts lower than before, and if
it grows slower than before, it must take longer to reach Economically, the present
value of future production has increased, so we should shift extraction towards the
future (see figure 1).
(b) the demand for the resource increases suddenly.
brief answer If the choke price remains unchanged this means that the demand curve
becomes flatter — greater demand at any price below In the case of the inverse
demand curve used in class, = − , this means that falls. If the price path
did not change we would extract more very period and total production would exceed
. So 0 must rise to dampen down the quantity demanded. Since prices still grow
at the rate it follows that 0 must also rise. If not, then we would reach before
exhaustion. You can also see this from the expression we derived in class for output:
= [1 − (1 + )− ],soif falls is higher. But this means that we must reach
4