Homework Assignment #1: Answer Key

Econ 497A
Energy Economics and Energy Security
Professor Ickes
Fall 2011
Homework Assignment #1: Answer Key
1. Suppose that the aggregate production function for the economy, = ( ) was Leontief
— that is the elasticity of substitution between and was zero. What does this imply
Brief Answer Zero elasticity of substitution means that there are no possibilities of substituting
inputs. Isoquants are L-shaped. We could write =min ³
´
where and are
technologically determined constants. Notice that is thus equal to the unit requirements
of capital per unit of output, for example. Suppose doubles but remains constant.
Then output will not increase.
(a) Now suppose that one of the factors, say , became increasingly scarce. What would
happen to the share of national income that would go to labor over time Explain.
brief answer If labor becomes increasingly scare the wage will increase relative to the
priceofcapital. Sinceincomecannotincreaseif is fixed must increase. So
labor’s share of income is rising.
(b) Suppose that the elasticity of substitution was extremely high (close to infinity). What
would this imply about the returns going to labor if it became exceedingly scarce Explain.
brief answer If the elasticity of substitution () is extremely high then it is easy to
substitute capital for labor. The production function with = ∞ leads to an isoquant
that is linear. So the production function could be written as = + . Wecan
substitute for without any changes in their marginal products. So the prices of
the factors will not change. If is increasing due to labor scarcity, but it is easy to
substitute capital for labor, the wage will not rise relative to the price of capital, so
will fall.
(c) Now suppose that as labor became more scarce its share of national income was unchanged.
What would the elasticity of substitution be in this case
brief answer If the share of national income is unchanged when labor becomes more
scarce it must mean that the wage must rise in exact proportion to the fall in labor.
Obviously this means that 0 ∞, from our answers to parts a and b. More
specifically, it means that =1 The elasticity of substitution is the elasticity of the
ratio of two inputs to a production function with respect to the ratio of their marginal
products. If the ratio of the marginal products changes exactly in proportion to the
ratio of the inputs then =1
1

2. (This question appears more difficult than it really is. Just read carefully, and follow along.
There are no mysteries here, but some interesting ideas.) Consider an economy with a production
function, = ( ) 1−− ,where is resources used in production, all other
variables are as usual, and are positive and + 1. Labor supply grows at the constant
rate, , and grows at the constant rate . We consume resources over time, so the growth
rate of ( ∆ )=−, where is a positive constant. From the production function it follows
that the growth rate of income is given by:
= + +(1− − )[ + ] (1)
where isthegrowthrateofincomeattime, etc. We are interested in a balanced growth
path where all the variables are growing at a constant rate and and grow at the same
rate. Using (1) solve for the balanced growth rate of income,
in terms of the parameters
of the model. Show that
is increasing in , for example.
brief answer By definition on a balanced growth path and aregrowingatthesamerate.
So = so using this in (1) we have:
=
+ +(1− − )[ + ]
=
− +(1− − )[ + ] (2)
where the second line follows from the definitions of the growth rates in the problem.
Solving (2) for
yields:
−
= (1− − )[ + ] −
(1 − − )[ + ] −
=
1 −
addition after class, Sept 22 I really should not have asked you do show that
is increasing
in First, you would need calculus which is not required for the course, and
second if you did differentiate (3) with respect to you would find it is negative not
positive. What I meant to ask is show that
is increasing in or and decreasing in
That would have been a better and easier question. I will grade accordingly.
(a) What happens to
if increases. Why How does
vary with
brief answer If increases resources are declining at a faster rate. From (3) it is
apparent that
falls. We can also see that if rises, so growth is more sensitive
to resources, then
also falls.
(b) The growth rate of output per worker is just − , so using your expression for
what is the expression for the growth rate of output per worker on the balanced growth
path,
Is this necessarily positive Explain.
brief answer Start with (3), and note that − = − , so
− ≡ − +(1− − )[ + ]
= −
1 −
− +(1− − )[ + ]
= − 1 −
1 −
1 −
2
(3)

=
− +(1− − )[ + ] − (1 − )
1 −
=
− +(1− − ) −
1 −
=
(1 − − ) − ( + )
1 −
(4)
from (4) it is apparent that the numerator can be positive or negative. If → 0
then
is necessarily positive. If 0 then
could be negative if resources
growth is sufficiently negative, for example. That is if is large enough. Intuitively,
if growth is sensitive to resources large and if resources are getting more scarce, it
can offset the benefits of technical progress, .
(c) Suppose there were resources were not fixed; instead suppose that they grow at the same
rate as population, so ∆
= . What would your expression for the balanced growth
path of output per worker (call it e
)looklikenow
brief answer Now resources are growing, so replace − with in (4), so we have
e (1 − − ) − ( − )
=
1 −
(1 − − )
= (5)
1 −
Resource growth is exactly offsetting the impact of labor growth in the expression.
Now the growth rate of per-capita income on the balanced growth path is necessarily
positive, because resources are always being augmented, and this offsets the negative
impact of population growth on per-capita income growth.
(d) Define the ”growth drag” from finite resources as the differencebetweengrowthinthe
hypothetical case of part (c) and the actual case of part (b). That is = e
− .
What is equal to Why is this likely to be a pretty small number
brief answer Using (4) and (5) we have
=
=
(1 − − )
−
1 −
( + )
1 −
(1 − − ) − ( + )
1 −
Parameters and are growth rates, numbers like 03 or something, is capital’s
share something like .4 or something, and is by definition less than one. So the
numerator is on the order of (2)(02 + 03) = 01 so is equal to something like
1
(01) ≈ 00167. Per-capita income growth tends to be much larger — at least an
1−4
order of magnitude; for example, in the US per-capita income growth has averaged
about 2% since 1959. The key point is that the drag from resources is likely to be
small, as long as is not very large.
(e) Expression (1) seems to indicate that if income is growing today, it will continue to grow
even as → 0. Why is this the case in this model What does the production function
imply about the elasticity of substitution
(6)
3

ief answer It must mean that the elasticity of substitution is at least unity. We can
substitute other inputs for declining resources without output falling. In fact, the
production function we have chosen has =1. We have assumed that resources are
notabindingconstraintongrowth. Butif1 then the share going to resource
owners would rise as resources became more scarce — in other words, would increase
as declined. So would not be a constant in (6), and thus your answer to part d
understates the effect of declining resources in the case where substitution is difficult.
We know from problem 1 that if production was Leontief then the share of national
income that would go to resource owners would increase dramatically as → 0
As your analysis in problem 1 shows, if =0then the share of income that goes
tothescarceresourcegoesto100%,so −→ 1, and the drag approaches + ,
which would overwhelm all sources of growth (it would still be true if 0 1).
This is clearly a result that is consistent with the apocalyptic intuition about resource
scarcity. When I wrote the production function as = ( ) 1−− I, in fact,
assumed that =1(with such a production function, called Cobb-Douglas, the factor
shares are independent of the capital labor ratio), as the shares and are constant.
But, in fact, we know that the share of income going to resource owners has actually
been falling in the US during the 20th century (real oil prices, for example, have
been roughly constant and energy consumption per unit of GDP has been falling).
So rather than 1 it seems almost certain that 1, and that the small drag
computed in part d is closer to the truth.
3. Consider the basic Hotelling model of exhaustible resources. Assume a competitive economy
with many producers, a fixed cost of extraction, , and a choke price, . The rate of interest
is given at rate . What happens to the extraction path of the resource (the plot of output,
,againsttime)if:
(a) the rate of interest falls.
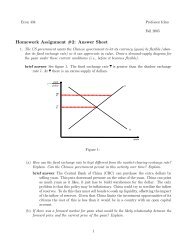
brief answer In class we analyzed a rise in , so this case is exactly opposite. If
falls, it is all of a sudden better to keep a dollar’s worth of oil in the ground than a
dollar in the bank. So oil production falls. This causes 0 to rise and 0 to fall. The
Hotelling Rule requires that net rent grows at the rate of interest which is now lower.
So clearly the time to exhaustion must rise. If price starts lower than before, and if
it grows slower than before, it must take longer to reach Economically, the present
value of future production has increased, so we should shift extraction towards the
future (see figure 1).
(b) the demand for the resource increases suddenly.
brief answer If the choke price remains unchanged this means that the demand curve
becomes flatter — greater demand at any price below In the case of the inverse
demand curve used in class, = − , this means that falls. If the price path
did not change we would extract more very period and total production would exceed
. So 0 must rise to dampen down the quantity demanded. Since prices still grow
at the rate it follows that 0 must also rise. If not, then we would reach before
exhaustion. You can also see this from the expression we derived in class for output:
= [1 − (1 + )− ],soif falls is higher. But this means that we must reach
4

q t
q 0
initial optimal
extraction path
q
0
new optimal
extraction path
T
T '
t
Figure 1: Shift in the Extraction Path
exhaustion at a lower , so the new extraction path must have higher 0 and lower
.
(c) the choke price falls
brief answer This means that is lower. If the price path were unchanged we would end
up with extra oil which cannot be optimal. So 0 must fall and 0 must increase. The
time to exhaustion must also fall, since reaches the new lower in less periods.
So 0 rises and falls.
(d) a tax on the sales (gross revenue) of the resource, per barrel is imposed on producers.
brief answer This is a tax on revenues, not on rents. So the producer is now equating
(1 − ) − = (1 − ) +1 −
1+
(7)
thetaxisclearlynotneutral(asitwouldbeifthetaxwereonrents,thenwecould
cancel out the (1 − ) terms). The impact of the tax is to lower the present value
of current profits relative to future profits, as the left-hand side of (7) fall by more
than the RHS. So the producer wants to produce less in the current period. So 0
falls. Since production is moved to the future the time to exhaustion must rise, since
prices still rise at the rate of interest.
(e) a new discovery of oil takes place that doubles reserves.
brief answer If reserves now equal 2, then production must rise. But if the choke
price is unchanged and prices grow at the rate of interest, then 0 must rise and
must increase as wellhso that the total amount of production Σ =0 −1 must rise. But
we know that = i 2 1 − (1 + )
−
then the sum of production is given by:
Σ =0 −1 = Σ =0
−1
2 [1 − (1 + )− ]=
so if doubles, and is given, the only thing that can rise is .
5