LECTURES ON ZARISKI VAN-KAMPEN THEOREM 1. Introduction ...

LECTURES ON ZARISKI VAN-KAMPEN THEOREM 31
A
B
D
C
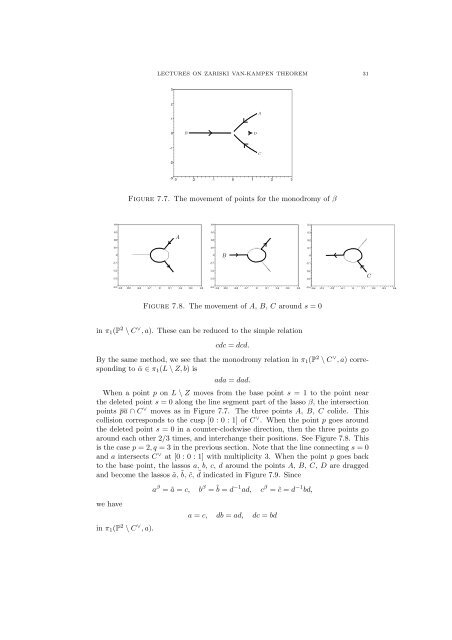
Figure 7.7. The movement of points for the monodromy of β
A
B
C
Figure 7.8. The movement of A, B, C around s =0
in π 1 (P 2 \ C ∨ ,a). These can be reduced to the simple relation
cdc = dcd.
By the same method, we see that the monodromy relation in π 1 (P 2 \ C ∨ ,a) corresponding
to ᾱ ∈ π 1 (L \ Z, b) is
ada = dad.
When a point p on L \ Z moves from the base point s = 1 to the point near
the deleted point s = 0 along the line segment part of the lasso β, the intersection
points pa ∩ C ∨ moves as in Figure 7.7. The three points A, B, C colide. This
collision corresponds to the cusp [0 :0:1]ofC ∨ . When the point p goes around
the deleted point s = 0 in a counter-clockwise direction, then the three points go
around each other 2/3 times, and interchange their positions. See Figure 7.8. This
is the case p =2,q = 3 in the previous section. Note that the line connecting s =0
and a intersects C ∨ at[0:0:1]with multiplicity 3. When the point p goes back
to the base point, the lassos a, b, c, d around the points A, B, C, D are dragged
and become the lassos ã, ˜b, ˜c, ˜d indicated in Figure 7.9. Since
a β =ã = c, b β = ˜b = d −1 ad, c β =˜c = d −1 bd,
we have
in π 1 (P 2 \ C ∨ ,a).
a = c, db = ad, dc = bd