Dynamic Performance of a SCARA Robot Manipulator With ...
Dynamic Performance of a SCARA Robot Manipulator With ...
Dynamic Performance of a SCARA Robot Manipulator With ...
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
IEEE TRANSACTIONS ON ROBOTICS, VOL. 25, NO. 1, FEBRUARY 2009 209<br />
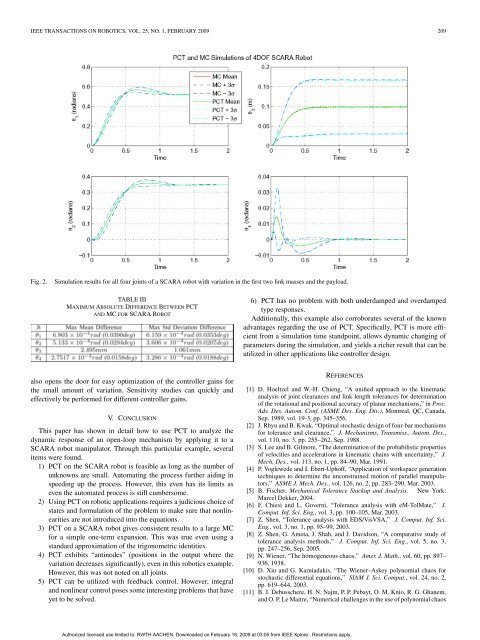
Fig. 2.<br />
Simulation results for all four joints <strong>of</strong> a <strong>SCARA</strong> robot with variation in the first two link masses and the payload.<br />
TABLE III<br />
MAXIMUM ABSOLUTE DIFFERENCE BETWEEN PCT<br />
AND MC FOR <strong>SCARA</strong> ROBOT<br />
6) PCT has no problem with both underdamped and overdamped<br />
type responses.<br />
Additionally, this example also corroborates several <strong>of</strong> the known<br />
advantages regarding the use <strong>of</strong> PCT. Specifically, PCT is more efficient<br />
from a simulation time standpoint, allows dynamic changing <strong>of</strong><br />
parameters during the simulation, and yields a richer result that can be<br />
utilized in other applications like controller design.<br />
also opens the door for easy optimization <strong>of</strong> the controller gains for<br />
the small amount <strong>of</strong> variation. Sensitivity studies can quickly and<br />
effectively be performed for different controller gains.<br />
V. CONCLUSION<br />
This paper has shown in detail how to use PCT to analyze the<br />
dynamic response <strong>of</strong> an open-loop mechanism by applying it to a<br />
<strong>SCARA</strong> robot manipulator. Through this particular example, several<br />
items were found.<br />
1) PCT on the <strong>SCARA</strong> robot is feasible as long as the number <strong>of</strong><br />
unknowns are small. Automating the process further aiding in<br />
speeding up the process. However, this even has its limits as<br />
even the automated process is still cumbersome.<br />
2) Using PCT on robotic applications requires a judicious choice <strong>of</strong><br />
states and formulation <strong>of</strong> the problem to make sure that nonlinearities<br />
are not introduced into the equations.<br />
3) PCT on a <strong>SCARA</strong> robot gives consistent results to a large MC<br />
for a simple one-term expansion. This was true even using a<br />
standard approximation <strong>of</strong> the trigonometric identities.<br />
4) PCT exhibits “antinodes” (positions in the output where the<br />
variation decreases significantly), even in this robotics example.<br />
However, this was not noted on all joints.<br />
5) PCT can be utilized with feedback control. However, integral<br />
and nonlinear control poses some interesting problems that have<br />
yet to be solved.<br />
REFERENCES<br />
[1] D. Hoeltzel and W.-H. Chieng, “A unified approach to the kinematic<br />
analysis <strong>of</strong> joint clearances and link length tolerances for determination<br />
<strong>of</strong> the rotational and positional accuracy <strong>of</strong> planar mechanisms,” in Proc.<br />
Adv. Des. Autom. Conf. (ASME Des. Eng. Div.), Montreal, QC, Canada,<br />
Sep. 1989, vol. 19-3, pp. 345–356.<br />
[2] J. Rhyu and B. Kwak, “Optimal stochastic design <strong>of</strong> four-bar mechanisms<br />
for tolerance and clearance,” J. Mechanisms, Transmiss., Autom. Des.,<br />
vol. 110, no. 3, pp. 255–262, Sep. 1988.<br />
[3] S. Lee and B. Gilmore, “The determination <strong>of</strong> the probabilistic properties<br />
<strong>of</strong> velocities and accelerations in kinematic chains with uncertainty,” J.<br />
Mech. Des., vol. 113, no. 1, pp. 84–90, Mar. 1991.<br />
[4] P. Voglewede and I. Ebert-Uph<strong>of</strong>f, “Application <strong>of</strong> workspace generation<br />
techniques to determine the unconstrained motion <strong>of</strong> parallel manipulators,”<br />
ASME J. Mech. Des., vol. 126, no. 2, pp. 283–290, Mar. 2003.<br />
[5] B. Fischer, Mechanical Tolerance Stackup and Analysis. New York:<br />
Marcel Dekker, 2004.<br />
[6] F. Chiesi and L. Governi, “Tolerance analysis with eM-TolMate,” J.<br />
Comput. Inf. Sci. Eng., vol. 3, pp. 100–105, Mar. 2003.<br />
[7] Z. Shen, “Tolerance analysis with EDS/VisVSA,” J. Comput. Inf. Sci.<br />
Eng., vol. 3, no. 1, pp. 95–99, 2003.<br />
[8] Z. Shen, G. Ameta, J. Shah, and J. Davidson, “A comparative study <strong>of</strong><br />
tolerance analysis methods,” J. Comput. Inf. Sci. Eng., vol. 5, no. 3,<br />
pp. 247–256, Sep. 2005.<br />
[9] N. Wiener, “The homogeneous chaos,” Amer. J. Math., vol. 60, pp. 897–<br />
936, 1938.<br />
[10] D. Xiu and G. Karniadakis, “The Wiener–Askey polynomial chaos for<br />
stochastic differential equations,” SIAM J. Sci. Comput., vol. 24, no. 2,<br />
pp. 619–644, 2003.<br />
[11] B.J.Debusschere,H.N.Najm,P.P.Pebayt,O.M.Knio,R.G.Ghanem,<br />
and O. P. Le Maitre, “Numerical challenges in the use <strong>of</strong> polynomial chaos<br />
Authorized licensed use limited to: RWTH AACHEN. Downloaded on February 18, 2009 at 03:05 from IEEE Xplore. Restrictions apply.