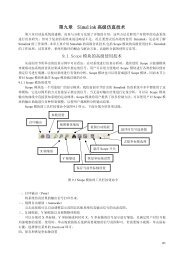
Assume that the local skin friction coefficient in turbulent flow is ...

Reading Assignment
Anderson, 3 rd edition: Chapter 15, pages 713 – 730, 738 – 740
Chapter 16, pages 745 – 751, 781 – 786
Anderson, 2 nd edition: Chapter 15, pages 637 – 655
Chapter 16, pages 669 – 676, 705 - 709
Problem 1 (40%)
Consider the two-dimensional incompressible flow between two rotating, concentric circles. The
inner cylinder has radius and rotates with angular velocity ω . The outer cylinder has radius
r0
0
r1
and rotates with angular velocity ω
1
. Assume that the resulting flow is steady and parallel
such that the radial velocity, V
r
, is equal to zero.
a) Using the continuity equation, show that the circumferential velocity, V , is independent of
θ
θ .
b) Using the circumferential momentum equation, and applying boundary conditions, determine
the circumferential velocity.
c) Without solving directly for the static pressure, use the radial momentum equation to show
that the static pressure must increase with increasing radius.
d) This type of device is often used to measure the dynamic viscosity of a fluid, µ , by
measuring the resulting moment acting on the cylinder. Given the moment acting on the
inner cylinder is M , determine the dynamic viscosity.
Problem 2 (20%)
a) Starting from the incompressible Navier-Stokes equations, derive the following ‘Bernoullilike’
equation:
r
∂
ρ
∂t
+ ∇⎜
⎛ p +
⎝
r
ρ V
V 1
2
2
The following vector calculus identities might be helpful:
r
r
V
r
2
∇ V
( V ⋅ ∇)
⎟
⎞
⎠
r
∇⎜
⎛ 2
1
=
2
V
⎝
r
= ∇ ∇ ⋅
r r r
= ρV
× ω − µ ∇ × ω
⎟
⎞
⎠
r r
− V × ω
r
( V ) − ∇ × ω

) Show that the total pressure,
flow.
r
p + , is constant along a streamline in a steady, inviscid
2
1
2
ρ V
c) Show that the total pressure is constant everywhere in a steady, inviscid, and irrotational
flow.
Problem 3 (40%)
p a
V w
p b
L
Consider the 2-D flow between two porous walls of length L at y = ± h . Assume that the length
of the walls is much larger than the half-height h so that the flow may be assumed to be constant
in the x-direction. The upper wall produces a suction such that the velocity normal to the wall is
V w
and is positive. Solve the incompressible Navier-Stokes equations to find the velocity and
pressure everywhere in duct for the case in which the pressure inlet and exit of the pipe are
p and p , respectively. Specifically, you should find the following solution for the x-velocity:
a
b
u
u
0
=
2
Re
⎛
⎜
⎝
y
h
− 1
+
Re Re
e − e
sinh Re
y
h
⎞
⎟
⎠
where u0
is a constant that you must determine as part of the solution and the Reynolds number
in this problem is defined as
V w
h Re =
.
ν
Plot u u0
for Re = 1, 10, and 100. Based on these plots, describe the basic behavior of the
velocity as a function of the Reynolds number.