Peripheral vision and pattern recognition: a review - strasburger - main

Peripheral_Vision.doc
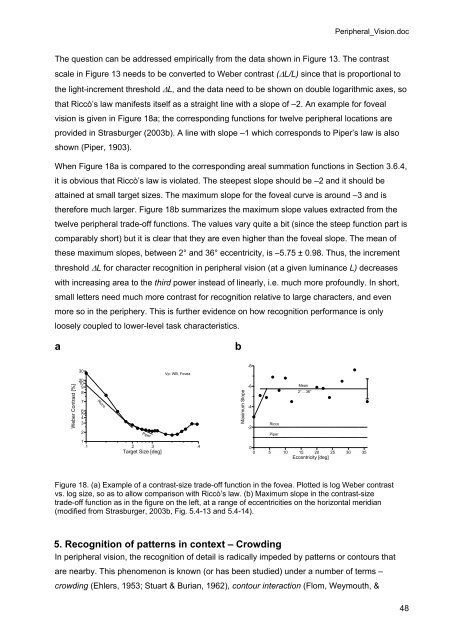
The question can be addressed empirically from the data shown in Figure 13. The contrast
scale in Figure 13 needs to be converted to Weber contrast (ΔL/L) since that is proportional to
the light-increment threshold ΔL, and the data need to be shown on double logarithmic axes, so
that Riccò’s law manifests itself as a straight line with a slope of –2. An example for foveal
vision is given in Figure 18a; the corresponding functions for twelve peripheral locations are
provided in Strasburger (2003b). A line with slope –1 which corresponds to Piper’s law is also
shown (Piper, 1903).
When Figure 18a is compared to the corresponding areal summation functions in Section 3.6.4,
it is obvious that Riccò’s law is violated. The steepest slope should be –2 and it should be
attained at small target sizes. The maximum slope for the foveal curve is around –3 and is
therefore much larger. Figure 18b summarizes the maximum slope values extracted from the
twelve peripheral trade-off functions. The values vary quite a bit (since the steep function part is
comparably short) but it is clear that they are even higher than the foveal slope. The mean of
these maximum slopes, between 2° and 36° eccentricity, is –5.75 ± 0.98. Thus, the increment
threshold ΔL for character recognition in peripheral vision (at a given luminance L) decreases
with increasing area to the third power instead of linearly, i.e. much more profoundly. In short,
small letters need much more contrast for recognition relative to large characters, and even
more so in the periphery. This is further evidence on how recognition performance is only
loosely coupled to lower-level task characteristics.
a
b
Weber Contrast [%]
30
20
10
9
8
7
6
5
4
3
2
1
Ricco
Piper
Vp: WB, Fovea
.1 .2 .3 .4
Target Size [deg]
Maximum Slope
-8
-6
-4
-2
0
Ricco
Piper
Mean
2°... 36°
0 5 10 15 20 25 30 35
Eccentricity [deg]
Figure 18. (a) Example of a contrast-size trade-off function in the fovea. Plotted is log Weber contrast
vs. log size, so as to allow comparison with Riccò’s law. (b) Maximum slope in the contrast-size
trade-off function as in the figure on the left, at a range of eccentricities on the horizontal meridian
(modified from Strasburger, 2003b, Fig. 5.4-13 and 5.4-14).
5. Recognition of patterns in context – Crowding
In peripheral vision, the recognition of detail is radically impeded by patterns or contours that
are nearby. This phenomenon is known (or has been studied) under a number of terms –
crowding (Ehlers, 1953; Stuart & Burian, 1962), contour interaction (Flom, Weymouth, &
48