- Page 1 and 2:
Numerical Recipes in C The Art of S
- Page 3 and 4:
Contents Preface to the Second Edit
- Page 5 and 6:
Contents vii 7.2 Transformation Met
- Page 7 and 8:
Contents ix 15.6 Confidence Limits
- Page 9 and 10:
Preface to the Second Edition Our a
- Page 11 and 12:
Preface to the Second Edition xiii
- Page 13 and 14:
Preface to the First Edition xv lin
- Page 15 and 16:
Types of License Offered License In
- Page 17 and 18:
Computer Programs by Chapter and Se
- Page 19 and 20:
Computer Programs by Chapter and Se
- Page 21 and 22:
Computer Programs by Chapter and Se
- Page 23 and 24:
Computer Programs by Chapter and Se
- Page 25 and 26:
Chapter 1. Preliminaries 1.0 Introd
- Page 27 and 28:
1.0 Introduction 3 Tested Machines
- Page 29 and 30:
1.1 Program Organization and Contro
- Page 31 and 32:
1.1 Program Organization and Contro
- Page 33 and 34:
true 1.1 Program Organization and C
- Page 35 and 36:
1.1 Program Organization and Contro
- Page 37 and 38:
1.1 Program Organization and Contro
- Page 39 and 40:
} 1.2 Some C Conventions for Scient
- Page 41 and 42:
1.2 Some C Conventions for Scientif
- Page 43 and 44:
1.2 Some C Conventions for Scientif
- Page 45 and 46:
(a) **m (b) **m 1.2 Some C Conventi
- Page 47 and 48:
1.2 Some C Conventions for Scientif
- Page 49 and 50:
1.2 Some C Conventions for Scientif
- Page 51 and 52:
1.2 Some C Conventions for Scientif
- Page 53 and 54:
= 0 3 = 0 = 0 = 0 = 0 = 0 1 ⁄ 2 1
- Page 55 and 56:
1.3 Error, Accuracy, and Stability
- Page 57 and 58:
2.0 Introduction 33 Accumulated rou
- Page 59 and 60:
2.0 Introduction 35 between singula
- Page 61 and 62:
2.1 Gauss-Jordan Elimination 37 Eli
- Page 63 and 64:
2.1 Gauss-Jordan Elimination 39 pre
- Page 65 and 66:
2.2 Gaussian Elimination with Backs
- Page 67 and 68:
2.3 LU Decomposition and Its Applic
- Page 69 and 70:
a b c d 2.3 LU Decomposition and It
- Page 71 and 72:
} 2.3 LU Decomposition and Its Appl
- Page 73 and 74:
2.3 LU Decomposition and Its Applic
- Page 75 and 76:
2.4 Tridiagonal and Band Diagonal S
- Page 77 and 78:
2.4 Tridiagonal and Band Diagonal S
- Page 79 and 80:
δx 2.5 Iterative Improvement of a
- Page 81 and 82:
2.5 Iterative Improvement of a Solu
- Page 83 and 84:
2.6 Singular Value Decomposition 59
- Page 85 and 86:
SVD of a Square Matrix 2.6 Singular
- Page 87 and 88:
solutions of A ⋅ x = d null space
- Page 89 and 90:
2.6 Singular Value Decomposition 65
- Page 91 and 92:
2.6 Singular Value Decomposition 67
- Page 93 and 94:
} 2.6 Singular Value Decomposition
- Page 95 and 96:
2.7 Sparse Linear Systems 2.7 Spars
- Page 97 and 98:
2.7 Sparse Linear Systems 73 prescr
- Page 99 and 100:
2.7 Sparse Linear Systems 75 Here
- Page 101 and 102:
2.7 Sparse Linear Systems 77 Finall
- Page 103 and 104:
2.7 Sparse Linear Systems 79 In row
- Page 105 and 106:
} 2.7 Sparse Linear Systems 81 jp=i
- Page 107 and 108:
2.7 Sparse Linear Systems 83 Matrix
- Page 109 and 110:
2.7 Sparse Linear Systems 85 while
- Page 111 and 112:
p=dvector(1,n); pp=dvector(1,n); r=
- Page 113 and 114:
} 2.7 Sparse Linear Systems 89 void
- Page 115 and 116:
2.8 Vandermonde Matrices and Toepli
- Page 117 and 118:
2.8 Vandermonde Matrices and Toepli
- Page 119 and 120:
2.8 Vandermonde Matrices and Toepli
- Page 121 and 122:
2.9 Cholesky Decomposition 97 If yo
- Page 123 and 124:
2.10 QR Decomposition 99 The standa
- Page 125 and 126:
#include #include "nrutil.h" 2.10
- Page 127 and 128:
in terms of which 2.11 Is Matrix In
- Page 129 and 130:
Chapter 3. Interpolation and Extrap
- Page 131 and 132:
(a) (b) 3.0 Introduction 107 Figure
- Page 133 and 134:
3.1 Polynomial Interpolation and Ex
- Page 135 and 136:
3.2 Rational Function Interpolation
- Page 137 and 138:
3.3 Cubic Spline Interpolation 113
- Page 139 and 140:
3.3 Cubic Spline Interpolation 115
- Page 141 and 142:
3.4 How to Search an Ordered Table
- Page 143 and 144:
} 3.4 How to Search an Ordered Tabl
- Page 145 and 146:
#include "nrutil.h" 3.5 Coefficient
- Page 147 and 148:
3.6 Interpolation in Two or More Di
- Page 149 and 150:
} int j; float *ymtmp; 3.6 Interpol
- Page 151 and 152:
3.6 Interpolation in Two or More Di
- Page 153 and 154:
Chapter 4. Integration of Functions
- Page 155 and 156:
4.1 Classical Formulas for Equally
- Page 157 and 158:
4.1 Classical Formulas for Equally
- Page 159 and 160:
4.1 Classical Formulas for Equally
- Page 161 and 162:
#define FUNC(x) ((*func)(x)) 4.2 El
- Page 163 and 164:
4.2 Elementary Algorithms 139 trapz
- Page 165 and 166:
4.4 Improper Integrals 141 which co
- Page 167 and 168:
4.4 Improper Integrals 143 The rout
- Page 169 and 170:
4.4 Improper Integrals 145 If you n
- Page 171 and 172:
4.5 Gaussian Quadratures and Orthog
- Page 173 and 174:
4.5 Gaussian Quadratures and Orthog
- Page 175 and 176:
Gauss-Legendre: Gauss-Chebyshev: Ga
- Page 177 and 178:
} 4.5 Gaussian Quadratures and Orth
- Page 179 and 180:
4.5 Gaussian Quadratures and Orthog
- Page 181 and 182:
4.5 Gaussian Quadratures and Orthog
- Page 183 and 184:
4.5 Gaussian Quadratures and Orthog
- Page 185 and 186:
4.6 Multidimensional Integrals 161
- Page 187 and 188:
y 4.6 Multidimensional Integrals 16
- Page 189 and 190:
Chapter 5. Evaluation of Functions
- Page 191 and 192:
5.1 Series and Their Convergence 16
- Page 193 and 194:
5.2 Evaluation of Continued Fractio
- Page 195 and 196:
5.2 Evaluation of Continued Fractio
- Page 197 and 198:
5.3 Polynomials and Rational Functi
- Page 199 and 200:
5.3 Polynomials and Rational Functi
- Page 201 and 202:
5.4 Complex Arithmetic 177 Actually
- Page 203 and 204:
5.5 Recurrence Relations and Clensh
- Page 205 and 206:
5.5 Recurrence Relations and Clensh
- Page 207 and 208:
5.6 Quadratic and Cubic Equations 1
- Page 209 and 210:
5.6 Quadratic and Cubic Equations 1
- Page 211 and 212:
5.7 Numerical Derivatives 187 With
- Page 213 and 214:
} 5.7 Numerical Derivatives 189 The
- Page 215 and 216:
Chebyshev polynomials 1 .5 0 −.5
- Page 217 and 218:
} 5.8 Chebyshev Approximation 193 f
- Page 219 and 220:
5.9 Derivatives or Integrals of a C
- Page 221 and 222:
5.10 Polynomial Approximation from
- Page 223 and 224:
5.11 Economization of Power Series
- Page 225 and 226:
5.12 Padé Approximants 201 then R(
- Page 227 and 228:
5.12 Padé Approximants 203 cof[2*n
- Page 229 and 230:
5.13 Rational Chebyshev Approximati
- Page 231 and 232:
5.13 Rational Chebyshev Approximati
- Page 233 and 234:
5.14 Evaluation of Functions by Pat
- Page 235 and 236:
5.14 Evaluation of Functions by Pat
- Page 237 and 238:
6.1 Gamma, Beta, and Related Functi
- Page 239 and 240:
6.1 Gamma, Beta, and Related Functi
- Page 241 and 242:
incomplete gamma function P(a,x) 1.
- Page 243 and 244:
} void nrerror(char error_text[]);
- Page 245 and 246:
#include 6.2 Incomplete Gamma Func
- Page 247 and 248:
6.3 Exponential Integrals 223 where
- Page 249 and 250:
6.3 Exponential Integrals 225 #incl
- Page 251 and 252:
6.4 Incomplete Beta Function 227 Th
- Page 253 and 254:
6.4 Incomplete Beta Function 229 So
- Page 255 and 256:
Bessel functions 1 .5 0 −.5 −1
- Page 257 and 258:
} 6.5 Bessel Functions of Integer O
- Page 259 and 260:
6.5 Bessel Functions of Integer Ord
- Page 261 and 262:
modified Bessel functions 4 3 2 1 6
- Page 263 and 264:
6.6 Modified Bessel Functions of In
- Page 265 and 266:
6.7 Bessel Functions of Fractional
- Page 267 and 268:
6.7 Bessel Functions of Fractional
- Page 269 and 270:
} 6.7 Bessel Functions of Fractiona
- Page 271 and 272:
6.7 Bessel Functions of Fractional
- Page 273 and 274:
} 6.7 Bessel Functions of Fractiona
- Page 275 and 276:
} 6.7 Bessel Functions of Fractiona
- Page 277 and 278:
6.8 Spherical Harmonics 253 The fir
- Page 279 and 280:
6.9 Fresnel Integrals, Cosine and S
- Page 281 and 282:
} 6.9 Fresnel Integrals, Cosine and
- Page 283 and 284:
} 6.10 Dawson’s Integral 259 } if
- Page 285 and 286:
6.11 Elliptic Integrals and Jacobia
- Page 287 and 288:
where 6.11 Elliptic Integrals and J
- Page 289 and 290:
#define TINY 1.0e-25 #define BIG 4.
- Page 291 and 292:
6.11 Elliptic Integrals and Jacobia
- Page 293 and 294:
#include #include "nrutil.h" 6.11
- Page 295 and 296:
6.12 Hypergeometric Functions 271 C
- Page 297 and 298:
#include "complex.h" #define ONE Co
- Page 299 and 300:
7.1 Uniform Deviates 275 As for ref
- Page 301 and 302:
7.1 Uniform Deviates 277 This corre
- Page 303 and 304:
#define IA 16807 #define IM 2147483
- Page 305 and 306:
RAN 3 1 7.1 Uniform Deviates 281 iy
- Page 307 and 308:
7.1 Uniform Deviates 283 from the w
- Page 309 and 310:
7.1 Uniform Deviates 285 Constants
- Page 311 and 312:
7.2 Transformation Method: Exponent
- Page 313 and 314:
7.2 Transformation Method: Exponent
- Page 315 and 316:
first random deviate in 7.3 Rejecti
- Page 317 and 318:
} 7.3 Rejection Method: Gamma, Pois
- Page 319 and 320:
} 7.3 Rejection Method: Gamma, Pois
- Page 321 and 322:
7.4 Generation of Random Bits 297 s
- Page 323 and 324:
} } *iseed
- Page 325 and 326:
7.5 Random Sequences Based on Data
- Page 327 and 328:
} } 7.5 Random Sequences Based on D
- Page 329 and 330:
7.6 Simple Monte Carlo Integration
- Page 331 and 332:
7.6 Simple Monte Carlo Integration
- Page 333 and 334:
7.7 Quasi- (that is, Sub-) Random S
- Page 335 and 336:
7.7 Quasi- (that is, Sub-) Random S
- Page 337 and 338:
} 7.7 Quasi- (that is, Sub-) Random
- Page 339 and 340:
7.7 Quasi- (that is, Sub-) Random S
- Page 341 and 342:
7.8 Adaptive and Recursive Monte Ca
- Page 343 and 344: 7.8 Adaptive and Recursive Monte Ca
- Page 345 and 346: 7.8 Adaptive and Recursive Monte Ca
- Page 347 and 348: } } 7.8 Adaptive and Recursive Mont
- Page 349 and 350: 7.8 Adaptive and Recursive Monte Ca
- Page 351 and 352: } 7.8 Adaptive and Recursive Monte
- Page 353 and 354: Chapter 8. Sorting 8.0 Introduction
- Page 355 and 356: 8.1 Straight Insertion and Shell’
- Page 357 and 358: 8.2 Quicksort 333 question of the b
- Page 359 and 360: 8.2 Quicksort 335 istack=lvector(1,
- Page 361 and 362: a 4 a 2 8.3 Heapsort 337 a 5 a 1 a
- Page 363 and 364: original array 1 2 3 4 5 6 14 8 32
- Page 365 and 366: 8.5 Selecting the Mth Largest 341 w
- Page 367 and 368: 8.5 Selecting the Mth Largest 343 r
- Page 369 and 370: } } } } 8.6 Determination of Equiva
- Page 371 and 372: Chapter 9. Root Finding and Nonline
- Page 373 and 374: 9.0 Introduction 349 good first gue
- Page 375 and 376: (a) (b) (c) (d) 9.1 Bracketing and
- Page 377 and 378: Bisection Method 9.1 Bracketing and
- Page 379 and 380: 9.2 Secant Method, False Position M
- Page 381 and 382: } 9.2 Secant Method, False Position
- Page 383 and 384: } 9.3 Van Wijngaarden-Dekker-Brent
- Page 385 and 386: 9.3 Van Wijngaarden-Dekker-Brent Me
- Page 387 and 388: 9.4 Newton-Raphson Method Using Der
- Page 389 and 390: 9.4 Newton-Raphson Method Using Der
- Page 391 and 392: } 9.4 Newton-Raphson Method Using D
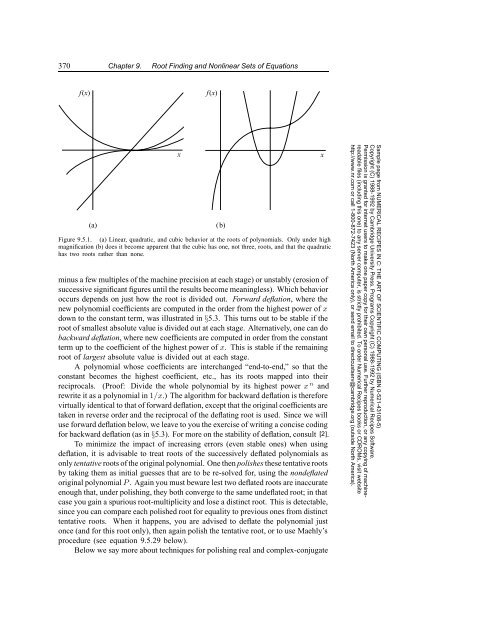
- Page 393: 9.5 Roots of Polynomials 9.5 Roots
- Page 397 and 398: 9.5 Roots of Polynomials 373 The me
- Page 399 and 400: Eigenvalue Methods 9.5 Roots of Pol
- Page 401 and 402: 9.5 Roots of Polynomials 377 of goi
- Page 403 and 404: 9.6 Newton-Raphson Method for Nonli
- Page 405 and 406: 9.6 Newton-Raphson Method for Nonli
- Page 407 and 408: 9.7 Globally Convergent Methods for
- Page 409 and 410: 9.7 Globally Convergent Methods for
- Page 411 and 412: 9.7 Globally Convergent Methods for
- Page 413 and 414: 9.7 Globally Convergent Methods for
- Page 415 and 416: 9.7 Globally Convergent Methods for
- Page 417 and 418: 9.7 Globally Convergent Methods for
- Page 419 and 420: X1 A B C 10.0 Introduction 395 D Fi
- Page 421 and 422: 10.1 Golden Section Search in One D
- Page 423 and 424: 10.1 Golden Section Search in One D
- Page 425 and 426: } } 10.1 Golden Section Search in O
- Page 427 and 428: 10.2 Parabolic Interpolation and Br
- Page 429 and 430: } 10.3 One-Dimensional Search with
- Page 431 and 432: 10.3 One-Dimensional Search with Fi
- Page 433 and 434: (a) (b) (c) (d) 10.4 Downhill Simpl
- Page 435 and 436: 10.4 Downhill Simplex Method in Mul
- Page 437 and 438: 10.5 Direction Set (Powell’s) Met
- Page 439 and 440: 10.5 Direction Set (Powell’s) Met
- Page 441 and 442: 10.5 Direction Set (Powell’s) Met
- Page 443 and 444: 10.5 Direction Set (Powell’s) Met
- Page 445 and 446:
(a) 10.6 Conjugate Gradient Methods
- Page 447 and 448:
10.6 Conjugate Gradient Methods in
- Page 449 and 450:
} 10.7 Variable Metric Methods in M
- Page 451 and 452:
10.7 Variable Metric Methods in Mul
- Page 453 and 454:
} 10.7 Variable Metric Methods in M
- Page 455 and 456:
10.8 Linear Programming and the Sim
- Page 457 and 458:
10.8 Linear Programming and the Sim
- Page 459 and 460:
10.8 Linear Programming and the Sim
- Page 461 and 462:
10.8 Linear Programming and the Sim
- Page 463 and 464:
10.8 Linear Programming and the Sim
- Page 465 and 466:
10.8 Linear Programming and the Sim
- Page 467 and 468:
} 10.8 Linear Programming and the S
- Page 469 and 470:
10.9 Simulated Annealing Methods 44
- Page 471 and 472:
(a) (b) (c) 1 .5 0 1 .5 0 1 .5 0 10
- Page 473 and 474:
} } 10.9 Simulated Annealing Method
- Page 475 and 476:
} free_ivector(jorder,1,ncity); #in
- Page 477 and 478:
10.9 Simulated Annealing Methods 45
- Page 479 and 480:
10.9 Simulated Annealing Methods 45
- Page 481 and 482:
Definitions and Basic Facts 11.0 In
- Page 483 and 484:
11.0 Introduction 459 In both the d
- Page 485 and 486:
11.0 Introduction 461 “Eigenpacka
- Page 487 and 488:
11.1 Jacobi Transformations of a Sy
- Page 489 and 490:
11.1 Jacobi Transformations of a Sy
- Page 491 and 492:
11.1 Jacobi Transformations of a Sy
- Page 493 and 494:
} } 11.2 Reduction of a Symmetric M
- Page 495 and 496:
11.2 Reduction of a Symmetric Matri
- Page 497 and 498:
11.2 Reduction of a Symmetric Matri
- Page 499 and 500:
11.3 Eigenvalues and Eigenvectors o
- Page 501 and 502:
11.3 Eigenvalues and Eigenvectors o
- Page 503 and 504:
11.3 Eigenvalues and Eigenvectors o
- Page 505 and 506:
} } 11.4 Hermitian Matrices 481 for
- Page 507 and 508:
11.5 Reduction of a General Matrix
- Page 509 and 510:
11.5 Reduction of a General Matrix
- Page 511 and 512:
11.6 The QR Algorithm for Real Hess
- Page 513 and 514:
11.6 The QR Algorithm for Real Hess
- Page 515 and 516:
11.6 The QR Algorithm for Real Hess
- Page 517 and 518:
11.7 Eigenvalues or Eigenvectors by
- Page 519 and 520:
11.7 Eigenvalues or Eigenvectors by
- Page 521 and 522:
and equation (12.0.1) looks like th
- Page 523 and 524:
⏐h(t)⏐ 2 (a) Ph( f ) (one-sided
- Page 525 and 526:
12.1 Fourier Transform of Discretel
- Page 527 and 528:
12.1 Fourier Transform of Discretel
- Page 529 and 530:
12.2 Fast Fourier Transform (FFT) 5
- Page 531 and 532:
12.2 Fast Fourier Transform (FFT) 5
- Page 533 and 534:
Other FFT Algorithms 12.2 Fast Four
- Page 535 and 536:
12.3 FFT of Real Functions, Sine an
- Page 537 and 538:
12.3 FFT of Real Functions, Sine an
- Page 539 and 540:
(a) (b) (c) +1 0 −1 +1 0 −1 +1
- Page 541 and 542:
#include 12.3 FFT of Real Function
- Page 543 and 544:
} 12.3 FFT of Real Functions, Sine
- Page 545 and 546:
} } } 12.4 FFT in Two or More Dimen
- Page 547 and 548:
data [1] Re Im 12.4 FFT in Two or M
- Page 549 and 550:
12.5 Fourier Transforms of Real Dat
- Page 551 and 552:
12.5 Fourier Transforms of Real Dat
- Page 553 and 554:
12.5 Fourier Transforms of Real Dat
- Page 555 and 556:
12.5 Fourier Transforms of Real Dat
- Page 557 and 558:
12.6 External Storage or Memory-Loc
- Page 559 and 560:
} } 12.6 External Storage or Memory
- Page 561 and 562:
Chapter 13. Fourier and Spectral Ap
- Page 563 and 564:
(t) r*s(t) 13.1 Convolution and Dec
- Page 565 and 566:
13.1 Convolution and Deconvolution
- Page 567 and 568:
13.1 Convolution and Deconvolution
- Page 569 and 570:
13.2 Correlation and Autocorrelatio
- Page 571 and 572:
13.3 Optimal (Wiener) Filtering wit
- Page 573 and 574:
log scale 13.4 Power Spectrum Estim
- Page 575 and 576:
13.4 Power Spectrum Estimation Usin
- Page 577 and 578:
13.4 Power Spectrum Estimation Usin
- Page 579 and 580:
amplitude 1 .8 .6 .4 .2 0 13.4 Powe
- Page 581 and 582:
13.4 Power Spectrum Estimation Usin
- Page 583 and 584:
13.5 Digital Filtering in the Time
- Page 585 and 586:
IIR (Recursive) Filters 13.5 Digita
- Page 587 and 588:
(a) (b) 13.5 Digital Filtering in t
- Page 589 and 590:
13.6 Linear Prediction and Linear P
- Page 591 and 592:
13.6 Linear Prediction and Linear P
- Page 593 and 594:
} 13.6 Linear Prediction and Linear
- Page 595 and 596:
13.6 Linear Prediction and Linear P
- Page 597 and 598:
13.7 Maximum Entropy (All Poles) Me
- Page 599 and 600:
13.8 Spectral Analysis of Unevenly
- Page 601 and 602:
13.8 Spectral Analysis of Unevenly
- Page 603 and 604:
13.8 Spectral Analysis of Unevenly
- Page 605 and 606:
} 13.8 Spectral Analysis of Unevenl
- Page 607 and 608:
} 13.8 Spectral Analysis of Unevenl
- Page 609 and 610:
13.9 Computing Fourier Integrals Us
- Page 611 and 612:
Cubic order: 13.9 Computing Fourier
- Page 613 and 614:
13.9 Computing Fourier Integrals Us
- Page 615 and 616:
13.10 Wavelet Transforms 591 The sp
- Page 617 and 618:
13.10 Wavelet Transforms 593 p.”
- Page 619 and 620:
13.10 Wavelet Transforms 595 comple
- Page 621 and 622:
} 13.10 Wavelet Transforms 597 wfil
- Page 623 and 624:
.2 0 −.2 .2 0 −.2 DAUB4 e10 + e
- Page 625 and 626:
wavelet amplitude 1.5 1 .5 .0001 10
- Page 627 and 628:
} nprev=nnew; } free_vector(wksp,1,
- Page 629 and 630:
13.10 Wavelet Transforms 605 Figure
- Page 631 and 632:
13.11 Numerical Use of the Sampling
- Page 633 and 634:
Chapter 14. Statistical Description
- Page 635 and 636:
14.1 Moments of a Distribution: Mea
- Page 637 and 638:
14.1 Moments of a Distribution: Mea
- Page 639 and 640:
14.2 Do Two Distributions Have the
- Page 641 and 642:
14.2 Do Two Distributions Have the
- Page 643 and 644:
14.2 Do Two Distributions Have the
- Page 645 and 646:
14.3 Are Two Distributions Differen
- Page 647 and 648:
14.3 Are Two Distributions Differen
- Page 649 and 650:
14.3 Are Two Distributions Differen
- Page 651 and 652:
14.3 Are Two Distributions Differen
- Page 653 and 654:
1. male 2. female . 14.4 Contingenc
- Page 655 and 656:
14.4 Contingency Table Analysis of
- Page 657 and 658:
14.4 Contingency Table Analysis of
- Page 659 and 660:
14.4 Contingency Table Analysis of
- Page 661 and 662:
14.5 Linear Correlation 637 two dis
- Page 663 and 664:
14.6 Nonparametric or Rank Correlat
- Page 665 and 666:
14.6 Nonparametric or Rank Correlat
- Page 667 and 668:
14.6 Nonparametric or Rank Correlat
- Page 669 and 670:
} } 14.7 Do Two-Dimensional Distrib
- Page 671 and 672:
14.7 Do Two-Dimensional Distributio
- Page 673 and 674:
#include #include "nrutil.h" 14.7
- Page 675 and 676:
14.8 Savitzky-Golay Smoothing Filte
- Page 677 and 678:
8 6 4 2 0 8 6 4 2 0 8 6 4 2 0 befor
- Page 679 and 680:
14.8 Savitzky-Golay Smoothing Filte
- Page 681 and 682:
15.1 Least Squares as a Maximum Lik
- Page 683 and 684:
15.1 Least Squares as a Maximum Lik
- Page 685 and 686:
15.2 Fitting Data to a Straight Lin
- Page 687 and 688:
15.2 Fitting Data to a Straight Lin
- Page 689 and 690:
#include #include "nrutil.h" 15.2
- Page 691 and 692:
15.3 Straight-Line Data with Errors
- Page 693 and 694:
15.3 Straight-Line Data with Errors
- Page 695 and 696:
15.4 General Linear Least Squares 6
- Page 697 and 698:
15.4 General Linear Least Squares 6
- Page 699 and 700:
} 15.4 General Linear Least Squares
- Page 701 and 702:
15.4 General Linear Least Squares 6
- Page 703 and 704:
15.4 General Linear Least Squares 6
- Page 705 and 706:
15.5 Nonlinear Models 681 Lawson, C
- Page 707 and 708:
15.5 Nonlinear Models 683 Note that
- Page 709 and 710:
15.5 Nonlinear Models 685 pivots, b
- Page 711 and 712:
#include "nrutil.h" 15.5 Nonlinear
- Page 713 and 714:
15.6 Confidence Limits on Estimated
- Page 715 and 716:
actual data set 15.6 Confidence Lim
- Page 717 and 718:
15.6 Confidence Limits on Estimated
- Page 719 and 720:
15.6 Confidence Limits on Estimated
- Page 721 and 722:
15.6 Confidence Limits on Estimated
- Page 723 and 724:
15.7 Robust Estimation 699 M� 1 C
- Page 725 and 726:
15.7 Robust Estimation 701 where th
- Page 727 and 728:
15.7 Robust Estimation 703 algorith
- Page 729 and 730:
} *a=aa; *b=bb; *abdev=abdevt/ndata
- Page 731 and 732:
Chapter 16. Integration of Ordinary
- Page 733 and 734:
16.0 Introduction 709 problem where
- Page 735 and 736:
y(x) 16.1 Runge-Kutta Method 711 1
- Page 737 and 738:
} 16.1 Runge-Kutta Method 713 yt=ve
- Page 739 and 740:
16.2 Adaptive Stepsize Control for
- Page 741 and 742:
16.2 Adaptive Stepsize Control for
- Page 743 and 744:
16.2 Adaptive Stepsize Control for
- Page 745 and 746:
16.2 Adaptive Stepsize Control for
- Page 747 and 748:
16.3 Modified Midpoint Method 723 H
- Page 749 and 750:
16.4 Richardson Extrapolation and t
- Page 751 and 752:
16.4 Richardson Extrapolation and t
- Page 753 and 754:
16.4 Richardson Extrapolation and t
- Page 755 and 756:
16.4 Richardson Extrapolation and t
- Page 757 and 758:
16.5 Second-Order Conservative Equa
- Page 759 and 760:
y 16.6 Stiff Sets of Equations 735
- Page 761 and 762:
16.6 Stiff Sets of Equations 737 If
- Page 763 and 764:
16.6 Stiff Sets of Equations 739 od
- Page 765 and 766:
} 16.6 Stiff Sets of Equations 741
- Page 767 and 768:
16.6 Stiff Sets of Equations 743 Co
- Page 769 and 770:
16.6 Stiff Sets of Equations 745 Se
- Page 771 and 772:
} 16.7 Multistep, Multivalue, and P
- Page 773 and 774:
16.7 Multistep, Multivalue, and Pre
- Page 775 and 776:
16.7 Multistep, Multivalue, and Pre
- Page 777 and 778:
Chapter 17. Two Point Boundary Valu
- Page 779 and 780:
equired boundary value 17.0 Introdu
- Page 781 and 782:
17.1 The Shooting Method 17.1 The S
- Page 783 and 784:
} 17.1 The Shooting Method 759 floa
- Page 785 and 786:
17.2 Shooting to a Fitting Point 76
- Page 787 and 788:
17.3 Relaxation Methods 763 depende
- Page 789 and 790:
X X X X X X X X X X X X X X X X X X
- Page 791 and 792:
17.3 Relaxation Methods 767 Next co
- Page 793 and 794:
17.3 Relaxation Methods 769 calcula
- Page 795 and 796:
} 17.3 Relaxation Methods 771 for (
- Page 797 and 798:
17.4 A Worked Example: Spheroidal H
- Page 799 and 800:
17.4 A Worked Example: Spheroidal H
- Page 801 and 802:
17.4 A Worked Example: Spheroidal H
- Page 803 and 804:
} 17.4 A Worked Example: Spheroidal
- Page 805 and 806:
17.4 A Worked Example: Spheroidal H
- Page 807 and 808:
17.5 Automated Allocation of Mesh P
- Page 809 and 810:
17.6 Handling Internal Boundary Con
- Page 811 and 812:
17.6 Handling Internal Boundary Con
- Page 813 and 814:
18.0 Introduction 789 is called a F
- Page 815 and 816:
18.1 Fredholm Equations of the Seco
- Page 817 and 818:
#include "nrutil.h" 18.1 Fredholm E
- Page 819 and 820:
18.2 Volterra Equations 795 in §18
- Page 821 and 822:
18.3 Integral Equations with Singul
- Page 823 and 824:
18.3 Integral Equations with Singul
- Page 825 and 826:
18.3 Integral Equations with Singul
- Page 827 and 828:
f (x) 1 .5 0 −.5 0 18.3 Integral
- Page 829 and 830:
18.4 Inverse Problems and the Use o
- Page 831 and 832:
18.4 Inverse Problems and the Use o
- Page 833 and 834:
18.5 Linear Regularization Methods
- Page 835 and 836:
18.5 Linear Regularization Methods
- Page 837 and 838:
18.5 Linear Regularization Methods
- Page 839 and 840:
18.6 Backus-Gilbert Method 815 nece
- Page 841 and 842:
18.6 Backus-Gilbert Method 817 Subs
- Page 843 and 844:
18.7 Maximum Entropy Image Restorat
- Page 845 and 846:
18.7 Maximum Entropy Image Restorat
- Page 847 and 848:
18.7 Maximum Entropy Image Restorat
- Page 849 and 850:
18.7 Maximum Entropy Image Restorat
- Page 851 and 852:
Chapter 19. Partial Differential Eq
- Page 853 and 854:
19.0 Introduction 829 possible stab
- Page 855 and 856:
y L ∆ y1 19.0 Introduction 831 A
- Page 857 and 858:
19.0 Introduction 833 So-called rap
- Page 859 and 860:
19.1 Flux-Conservative Initial Valu
- Page 861 and 862:
19.1 Flux-Conservative Initial Valu
- Page 863 and 864:
19.1 Flux-Conservative Initial Valu
- Page 865 and 866:
19.1 Flux-Conservative Initial Valu
- Page 867 and 868:
19.1 Flux-Conservative Initial Valu
- Page 869 and 870:
t or n 19.1 Flux-Conservative Initi
- Page 871 and 872:
19.2 Diffusive Initial Value Proble
- Page 873 and 874:
19.2 Diffusive Initial Value Proble
- Page 875 and 876:
and the heuristic stability criteri
- Page 877 and 878:
19.3 Initial Value Problems in Mult
- Page 879 and 880:
19.3 Initial Value Problems in Mult
- Page 881 and 882:
19.4 Fourier and Cyclic Reduction M
- Page 883 and 884:
19.4 Fourier and Cyclic Reduction M
- Page 885 and 886:
19.4 Fourier and Cyclic Reduction M
- Page 887 and 888:
FACR Method 19.5 Relaxation Methods
- Page 889 and 890:
19.5 Relaxation Methods for Boundar
- Page 891 and 892:
19.5 Relaxation Methods for Boundar
- Page 893 and 894:
19.5 Relaxation Methods for Boundar
- Page 895 and 896:
19.6 Multigrid Methods for Boundary
- Page 897 and 898:
19.6 Multigrid Methods for Boundary
- Page 899 and 900:
S S S E γ = 1 19.6 Multigrid Metho
- Page 901 and 902:
19.6 Multigrid Methods for Boundary
- Page 903 and 904:
19.6 Multigrid Methods for Boundary
- Page 905 and 906:
} 19.6 Multigrid Methods for Bounda
- Page 907 and 908:
19.6 Multigrid Methods for Boundary
- Page 909 and 910:
19.6 Multigrid Methods for Boundary
- Page 911 and 912:
#include 19.6 Multigrid Methods fo
- Page 913 and 914:
Chapter 20. Less-Numerical Algorith
- Page 915 and 916:
20.1 Diagnosing Machine Parameters
- Page 917 and 918:
20.1 Diagnosing Machine Parameters
- Page 919 and 920:
(a) G(i) (b) MSB 4 3 2 1 0 LSB i MS
- Page 921 and 922:
20.3 Cyclic Redundancy and Other Ch
- Page 923 and 924:
20.3 Cyclic Redundancy and Other Ch
- Page 925 and 926:
20.3 Cyclic Redundancy and Other Ch
- Page 927 and 928:
} 20.4 Huffman Coding and Compressi
- Page 929 and 930:
20.4 Huffman Coding and Compression
- Page 931 and 932:
} 20.4 Huffman Coding and Compressi
- Page 933 and 934:
} } } 20.4 Huffman Coding and Compr
- Page 935 and 936:
1.0 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2
- Page 937 and 938:
20.5 Arithmetic Coding 913 Individu
- Page 939 and 940:
20.6 Arithmetic at Arbitrary Precis
- Page 941 and 942:
} for (j=n;j>=1;j--) { ireg=u[j]+HI
- Page 943 and 944:
#include "nrutil.h" #define RX 256.
- Page 945 and 946:
} 20.6 Arithmetic at Arbitrary Prec
- Page 947 and 948:
20.6 Arithmetic at Arbitrary Precis
- Page 949:
20.6 Arithmetic at Arbitrary Precis