Chapter 4 Shear Forces and Bending Moments
Chapter 4 Shear Forces and Bending Moments
Chapter 4 Shear Forces and Bending Moments
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
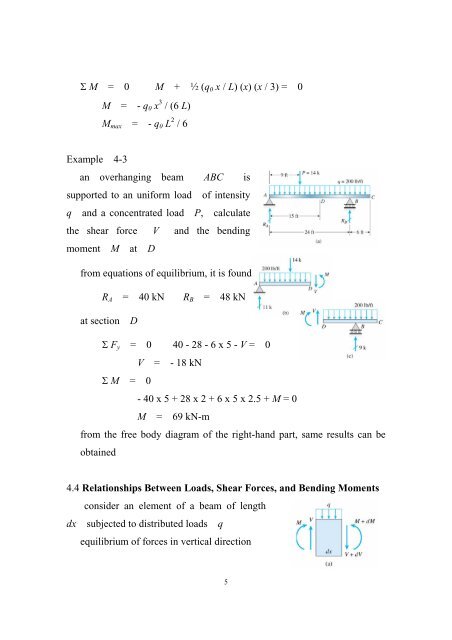
M = 0 M + 2 (q 0 x / L) (x) (x / 3) = 0M = - q 0 x 3 / (6 L)M max = - q 0 L 2 / 6Example 4-3an overhanging beam ABC issupported to an uniform load of intensityq <strong>and</strong> a concentrated load P, calculatethe shear force V <strong>and</strong> the bendingmoment M at Dfrom equations of equilibrium, it is foundR A = 40 kNR B = 48 kNat section D F y = 0 40 - 28 - 6 x 5 - V = 0V = - 18 kN M = 0- 40 x 5 + 28 x 2 + 6 x 5 x 2.5 + M = 0M = 69 kN-mfrom the free body diagram of the right-h<strong>and</strong> part, same results can beobtained4.4 Relationships Between Loads, <strong>Shear</strong> <strong>Forces</strong>, <strong>and</strong> <strong>Bending</strong> <strong>Moments</strong>consider an element of a beam of lengthdx subjected to distributed loads qequilibrium of forces in vertical direction5