Chapter 5: Exercises with Solutions

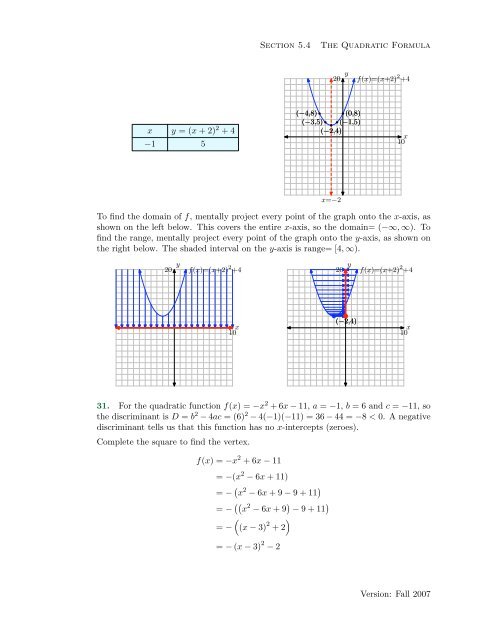
Section 5.4The Quadratic Formulay20 f(x)=(x+2) 2 +4x y = (x + 2) 2 + 4−1 5(−4,8)(0,8)(−3,5)(−1,5)(−2,4)x10x=−2To find the domain of f, mentally project every point of the graph onto the x-axis, asshown on the left below. This covers the entire x-axis, so the domain= (−∞, ∞). Tofind the range, mentally project every point of the graph onto the y-axis, as shown onthe right below. The shaded interval on the y-axis is range= [4, ∞).y20 f(x)=(x+2) 2 +4y20 f(x)=(x+2) 2 +4x10(−2,4)x1031. For the quadratic function f(x) = −x 2 + 6x − 11, a = −1, b = 6 and c = −11, sothe discriminant is D = b 2 − 4ac = (6) 2 − 4(−1)(−11) = 36 − 44 = −8 < 0. A negativediscriminant tells us that this function has no x-intercepts (zeroes).Complete the square to find the vertex.f(x) = −x 2 + 6x − 11= −(x 2 − 6x + 11)= − ( x 2 − 6x + 9 − 9 + 11 )= − (( x 2 − 6x + 9 ) − 9 + 11 )()= − (x − 3) 2 + 2= − (x − 3) 2 − 2Version: Fall 2007