Chapter 05.03 Newton's Divided Difference Interpolation – More ...

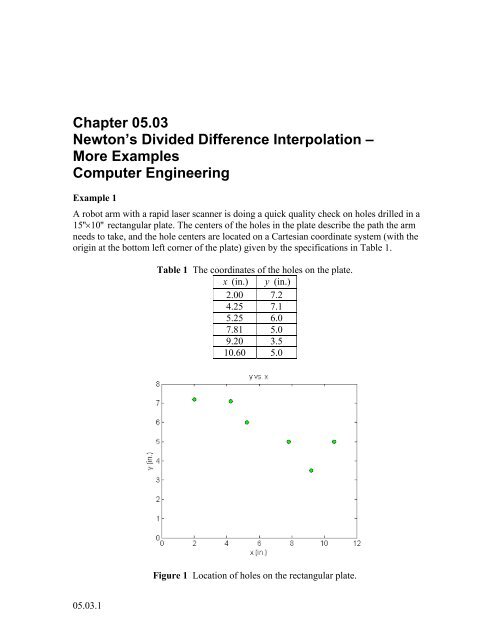
05.03.2 Chapter 05.03If the laser is traversing from x 2. 00 to x 4. 25 in a linear path, what is the value of y atx 4.00 using Newton’s divided difference method of interpolation and a first orderpolynomial?SolutionFor linear interpolation, the value of y is given byy( x) b0 b1( x x0)Since we want to find the value of y at x 4. 00 , using the two points x 2. 00 andx 4.25, thenx 2.00, ( ) 7. 20y x0 x 4.25, ( ) 7. 11y x1 givesb 0 y( x 0) 7.2y ( x1) y ( x0)b1x1x07.17.24.25 2.00 0.044444Hencey( x) b0 b1( x x0) 7.2 0.044444( x 2.00), 2.00 x 4. 25At x 4. 00x ( 4.00) 7.2 0.044444(4.00 2.00) 7.1111 in.If we expandy ( x) 7.2 0.044444( x 2.00), 2.00 x 4. 25we gety( x) 7.2889 0.044444x,2.00 x 4. 25This is the same expression that was obtained with the direct method.Example 2A robot arm with a rapid laser scanner is doing a quick quality check on holes drilled in a15" 10" rectangular plate. The centers of the holes in the plate describe the path the armneeds to take, and the hole centers are located on a Cartesian coordinate system (with theorigin at the bottom left corner of the plate) given by the specifications in Table 2.

05.03.4 Chapter 05.03y( x) b0 b1( x x0) b2( x x0)( x x1) 7.2 0.044444( x 2.00) 0.32479( x 2.00)( x 4.25), 2.00 x 5. 25At x 4. 00y ( 4.00) 7.2 0.044444(4.00 2.00) 0.32479(4.00 2.00)(4.00 4.25) 7.2735 in.The absolute relative approximate error aobtained between the results from the first andsecond order polynomial is7.2735 7.1111 a1007.2735 2.2327%If we expand,y ( x) 7.2 0.044444( x 2.00) 0.32479( x 2.00)( x 4.25), 2.00 x 5. 25we get2y(x) 4.5282 1.9855x 0.32479x,2.00 x 5. 25This is the same expression that was obtained with the direct method.Example 3A robot arm with a rapid laser scanner is doing a quick quality check on holes drilled in a15" 10" rectangular plate. The centers of the holes in the plate describe the path the armneeds to take, and the hole centers are located on a Cartesian coordinate system (with theorigin at the bottom left corner of the plate) given by the specifications in Table 3.Table 3 The coordinates of the holes on the plate.x (in.) y (in.)2.00 7.24.25 7.15.25 6.07.81 5.09.20 3.510.60 5.0Find the path traversed through the six points using Newton’s divided difference method ofinterpolation and a fifth order polynomial.SolutionFor a fifth order polynomial, the value of y is given byy(x) b b ( x x ) b ( x x )( x x ) b ( x x01020)( x x )( x x b4( x x0)( x x1)(x x2)( x x3) b5( x x0)( x x1)(x x2)( x x3)(x x4)Using the six points,x0 2.00, y ( x 0) 7. 2x 4.25, ( ) 7. 11y x1 13012)

Newton’s Divided Difference Interpolation-More Examples: Computer Engineering 05.03.5givesx 5.25,2y ( x ) 6. 02x3 7.81, y ( x 3) 5. 0x 9.20,4y ( x ) 3. 54x5 10.60, y ( x 5) 5. 0b y[ 0]0x y( x 0) 7.2b y x , ]1[1x0y(x1 ) y(x0)x1 x07.17.24.25 2.00 0.044444b y x , x , ]2[2 1x0y[x2 , x1] y[x1,x0]x2 xy(x2) y(x1)y[x2, x1] x2 x16.0 7.15.25 4.25 1.1y x , x ] 0.044444[1 00y[x2, x1] y[x1,x0]b2x2 x01.10.0444445.25 2.00 0.32479b y x , x , x , ]3[3 2 1x0y[x3 , x2, x1] y[x2, x1,x0]y[x3y[x3, x, x22, x ] 1x3y[x x30, x2x] y[x3 xy(x3) y(x2)] x3 x25.0 6.07.815.25 0.3906312, x ]1

05.03.6 Chapter 05.03121212)()(],[xxxyxyxxy4.255.257.16.01.1131223123],[],[],,[xxxxyxxyxxxy4.257.811.10.390630.199260.32479],,[ 012 xxxy],,,[ 01233 xxxxyb 03012123 ],,[],,[xxxxxyxxxy2.007.810.324790.199260.090198],,,,[ 012344 xxxxxyb 0401231234 ],,,[],,,[xxxxxxyxxxxy141232341234],,[],,[],,,[xxxxxyxxxyxxxxy242334234],[],[],,[xxxxyxxyxxxy343434)()(],[xxxyxyxxy7.819.205.03.51.07910.39063],[ 23 xxy242334234],[],[],,[xxxxyxxyxxxy5.259.200.390631.07910.174310.19926],,[ 123 xxxy

Newton’s Divided Difference Interpolation-More Examples: Computer Engineering 05.03.7141232341234],,[],,[],,,[xxxxxyxxxyxxxxy4.259.200.199260.174310.0754690.090198],,,[ 0123 xxxxy04012312344],,,[],,,[xxxxxxyxxxxyb2.009.200.0901980.0754690.023009],,,,,[ 0123455 xxxxxxyb 050123412345 ],,,,[],,,,[xxxxxxxyxxxxxy151234234512345],,,[],,,[],,,,[xxxxxxyxxxxyxxxxxy252343452345],,[],,[],,,[xxxxxyxxxyxxxxy353445345],[],[],,[xxxxyxxyxxxy454545)()(],[xxxyxyxxy9.2010.603.55.01.07141.0791],[ 34 xxy353445345],[],[],,[xxxxyxxyxxxy7.8110.601.07911.07140.770810.17431],,[ 234 xxxy252343452345],,[],,[],,,[xxxxxyxxxyxxxxy5.2510.600.174310.770810.17666

05.03.8 Chapter 05.030.075469],,,[ 1234 xxxxy151234234512345],,,[],,,[],,,,[xxxxxxyxxxxyxxxxxy4.2510.600.0754690.176660.0397050.023009],,,,[ 01234 xxxxxy0501234123455],,,,[],,,,[xxxxxxxyxxxxxyb2.0010.600.0230090.0397050.0072923Hence))()()()(())()()(())()(())(()()(432105321042103102010xxxxxxxxxxbxxxxxxxxbxxxxxxbxxxxbxxbbxy9.2)7.81)(5.25)(4.25)(2)(0.0072923(7.81)5.25)(4.25)(2)(0.023009(5.25)4.25)(2)(0.090198(4.25)2)(0.32479(2)0.04444(7.2xxxxxxxxxxxxxxxExpanding this formula, we get10.62,0.00729230.230912.786215.85541.34430.898)(5432 xxxxxxxyThis is the same expression that was obtained with the direct method.

Newton’s Divided Difference Interpolation-More Examples: Computer Engineering 05.03.9Figure 2 Fifth order polynomial to traverse points of robot path (usingdirect method of interpolation).INTERPOLATIONTopic Newton’s Divided Difference InterpolationSummary Examples of Newton’s divided difference interpolation.Major Computer EngineeringAuthors Autar KawDate November 23, 2009Web Site http://numericalmethods.eng.usf.edu