Chapter 12 Notes

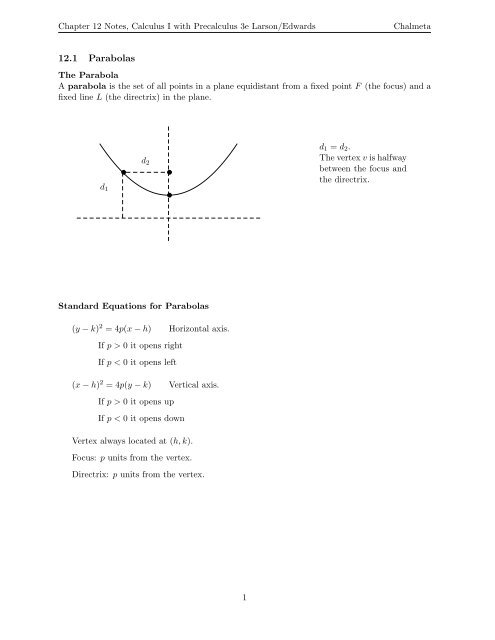
Chapter 12 Notes, Calculus I with Precalculus 3e Larson/EdwardsChalmeta12.1 ParabolasThe ParabolaA parabola is the set of all points in a plane equidistant from a fixed point F (the focus) and afixed line L (the directrix) in the plane.d 1 = d 2 .d 2Thevertexv ishalfway✉ ✉between the focus andthe directrix.d 1✉Standard Equations for Parabolas(y −k) 2 = 4p(x−h) Horizontal axis.If p > 0 it opens rightIf p < 0 it opens left(x−h) 2 = 4p(y −k) Vertical axis.If p > 0 it opens upIf p < 0 it opens downVertex always located at (h,k).Focus: p units from the vertex.Directrix: p units from the vertex.1

Chapter 12 Notes, Calculus I with Precalculus 3e Larson/EdwardsChalmetaExample 12.1.1. Find the vertex, focus and directrix for the parabola and sketch the graph.y 2 +6y +8x+25 = 0.We want the equation to be in form (y−k) 2 = 4p(x−h) so we need to complete the square.321−8−7−6−5−4−3−2−1 −1−2−3−4−5−6−7−8−91 2 32

Chapter 12 Notes, Calculus I with Precalculus 3e Larson/EdwardsChalmetaExample 12.1.2. Find the standard form of the equation of the parabola with its vertex at theorigin and directrix y = −3Step 1: Graph the parabola so that we know what it looks like.Example 12.1.3. Find the standard form of the parabola with vertex (-1, 2) and focus (-1, 0).Sketch the parabola.4321−4−3−2−1−11 2 3 4−2−3−43

Chapter 12 Notes, Calculus I with Precalculus 3e Larson/EdwardsChalmetaExample 12.1.4. Find the vertex, focus and directrix for the parabola and sketch the graph.Step 1: Clear the denominator.y = 1 4 (x2 −2x+5).654321−3−2−1−11 2 3 4 5 6−2−34

Chapter 12 Notes, Calculus I with Precalculus 3e Larson/EdwardsChalmeta12.2 EllipseAn ellipse is the set of all points P in a plane such that the sum of the distances of P from twofixed points (F and F ′ ) in the plane is constant. F and F ′ are called the foci (plural of focus).vF F v ′(h,k)d 1 +d 2 = constant.F and F ′ are the foci.v and v ′ are vertices.(h,k) is the center.Label the diagram above with the following:1. major axis2. minor axis3. minor axis vertices: B and B ′4. distance from foci to center: c5. distance from vertices to center: a (major axis) and b (minor axis)By using the distance formula we can derive a generic equation for an ellipse.Standard Equations for EllipseCenter always located at (h,k).⎫Major axis length: 2a ⎬Minor axis length: 2b ⎭ 0 < b < a.Horizontal major axis.Vertical major axis.(x−h) 2a 2+(y −k)2b 2 = 1(x−h) 2b 2+(y −k)2a 2 = 1The foci lie on the major axis c units from the center withc 2 = a 2 −b 2 .5

Chapter 12 Notes, Calculus I with Precalculus 3e Larson/EdwardsChalmetaExample 12.2.1. Sketch the graph, find the foci, and the lengths of the major and minor axesforx 24 + y29 = 1.54321−4−3−2−1−11 2 3 4−2−3−4−5Example 12.2.2. Sketch the graph, find the foci, and the lengths of the major and minor axesforx 2 +9y 2 = 9.321−4−3−2−1−11 2 3 4−2−36

Chapter 12 Notes, Calculus I with Precalculus 3e Larson/EdwardsChalmetaExample 12.2.3. Sketch the graph, find the foci, and the lengths of the major and minor axesfor9x 2 +4y 2 −54x+40y +37 = 0.Need:for the y’s.(x−h) 2a 2+(y −k)2b 2= 1 so we complete the square, twice. Once for the x’s and once2−4−22 4 6−2−4−6−8−107

Chapter 12 Notes, Calculus I with Precalculus 3e Larson/EdwardsChalmetaExample 12.2.4. Find the standard form of the equation of the ellipse withCenter (3, 2),Foci: (1, 2) and (5, 2) anda = 3c.8642−4−22 4 6 8 10−2−4−68

Chapter 12 Notes, Calculus I with Precalculus 3e Larson/EdwardsChalmeta12.3 HyperbolaA hyperbola is the set of all points P in a plane such that the absolute value of the differencesof the distances of P to two fixed points (F and F ′ ) in the plane is positive constant. F and F ′are called the foci (plural of focus).F vv ′x 2a 2 − y2b 2 = 1Center (0, 0)x-int: (-a, 0) and (a, 0)F ′ y-int: NONEFoci: F (-c, 0) and F ′ (c, 0).c 2 = a 2 +b 2Transverse axis length = 2aConjugate axis length = 2bvy 2a 2 − x2b 2 = 1F ′ Center (0, 0)x-int: NONEy-int: (0,-a) and (0,a)Foci: F (0,-c) and F ′ (0,c).v ′ Fc 2 = a 2 +b 2Transverse axis length = 2aConjugate axis length = 2b9

Chapter 12 Notes, Calculus I with Precalculus 3e Larson/EdwardsChalmetaExample 12.3.1. Sketch, find foci and axis lengths for6y 24 − x29 = 142−6−4−22 4 6−2−4−6Example 12.3.2. Sketch, find foci and axis lengths for69y 2 −16x 2 = 14442−6−4−22 4 6−2−4−610

Chapter 12 Notes, Calculus I with Precalculus 3e Larson/EdwardsChalmetaStandard Equations for HyperbolaCenter always located at (h,k).⎫Transverse axis length: 2a ⎬Conjugate axis length: 2b ⎭ a > 0 and b > 0Horizontal transverse axis. (x-intercepts) Vertical transverse axis. (y-intercepts)(x−h) 2a 2−(y −k)2b 2 = 1(y −k) 2a 2− (x−h)2b 2 = 1(h,k)F ′vF v v ′ F′ (h,k)v ′ FThe foci lie on the transverse axis c units from the center withc 2 = a 2 +b 2 .The asymptote ”‘box”’ for drawing is determined by±a along the transverse axis from the center±b along the conjugate axis from the center11

Chapter 12 Notes, Calculus I with Precalculus 3e Larson/EdwardsChalmetaExample 12.3.3. Convert to a standard equation and graph the following:−9x 2 +16y 2 −72x−96y −144 = 0108642−18−16−14−12−10−8−6−4−22 4 6 8−2−4−612

Chapter 12 Notes, Calculus I with Precalculus 3e Larson/EdwardsChalmetaExample 12.3.4. Convert to a standard equation and graph the following:x 2 −9y 2 +36y −72 = 08642−14−12−10−8−6−4−22 4 6 8 10 12 14−2−4−6−813