Note on Adjustment and the Specific Factor Model

More documents

Recommendations

Info

• the problem of course, is that in all transition economies labor productivityfell faster than output, and this is especially so in the statesector. 3In the long-run both capital and labor can adjust. Full adjustment meansthat capital moves to the private sector; hence, the demand for labor in theprivate sector increases. The full adjustment equilibrium is at point E andE 0 .1.0.1 AssessmentNotice that this type of model explains output losses due to unemploymentof resources. But in transition economies labor productivity has fallen, asemployment fell by much less than output. Hence, we also need to explainwhy labor productivity fell. This is one of the virtues of a disorganizationtypeof explanation.An alternative explanation of this puzzle is that the state Þrm does notlay off workers, but continues to produce via subsidies. There may be nopurchasers, and inventories build up. The price of the output has also fallen.Hence, labor productivity falls.Notice that this type of model tells us that we need to focus on severalitems:1. What determines the rate of contraction in the state sector? Presumably,this is related to the magnitude of the initial distortion, the speedwith which subsidies are ended, and the means of enterprise survival.2. What determines the rate of private sector expansion? Presumably thisdepends on the legal infrastructure for the private sector — how easy isit to start new Þrms — corruption, corporate governance.3. What determines the pace at which capital can ßow from the state tothe private sector? Again this will depend on the Þnancial system, legalsystem, corporate governance.3 This is one more reason why we need some explanation of output dynamics thatfocuses on changes in efficiency. This could be disorganization, for example, or it could berevelation of past inefficiency.4
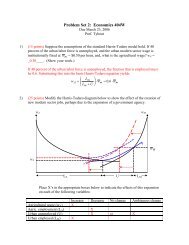
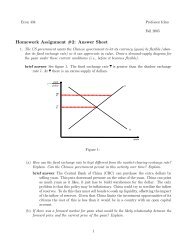
2 Structural AdjustmentStructural change and structural adjustment is an important explanationof transition. The basic idea is that the move to hard budget constraintscauses declines in production in those sectors experiencing a decline in relativeprices, combined with a slower expansion of those sectors that experiencean increase in relative prices.The basic argument is that it takes time for structural adjustment to takeplace. Another way to say this is that resources will be unemployed duringsome period of the transition. From a simple arithmetic point of view, theinitial preponderance of the state sector means that enormous growth of theprivate sector is needed to offset contraction.∆yy= µ∆Xs X s+(1 − µ) ∆XpX p (2)where µ is the share in the state sector, and ∆X p is the change in output inthe private sector. Then for the rate of output growth to be constant,∆Xµp1 − µ = − X p. (3)∆X sX sIf we start from a situation where the state sector was 90% of total production(an underestimate, to be sure!), then if the state sector is declining at 10% ayear, the private sector must expand at 90% per year to keep output growthconstant.How does private and public sector production coincide if the former ismore productive? It is easiest to begin with the case where the goods arethe same, and the different ownership form affects quality or cost. Supposethat the latter is of poorer quality, and let θ measure this difference; hence,P p = P s (1 + θ). If consumers purchase both types of goods, then it must bethat subsidies and taxes (the excess tax burden on the private sector) mustoffset the quality differential. Thus, we must have P p (1 − t) =P s (1 + σ). Itthen follows that1 + θ = 1 + σ1 − t . (4)From 4 it follows that elimination of the subsidy or of the tax on privateproduction would disturb the equilibrium between the two sectors.We can use 4 to illustrate two aspects of transition. We can think ofrestructuring as the process of improving the former state-owned enterprises.5
Page 1: Note on Adjustment
Page 6 and 7: In short-hand this can be thought o
Page 8 and 9: • the real wage decreasesNotice t
Page 10 and 11: the state sector depends on the pro

Note on Adjustment and the Specific Factor Model

Create successful ePaper yourself

Delete template?

Save as template?