Plastic model with non-local damage applied to concrete

More documents

Recommendations

Info

78P. GRASSL AND M. JIRÁSEKwhere c c is the dilation coefficient. The plastic hardening variable is defined by the rate equationrffiffirffiffiffi2 2’k p ¼ jj’e p jj ¼ ’l @g p3 3 @%r ¼ l ’ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi1=3 þ 2c 2 cð17Þwhich means that the scaling factor from (3) is for this particular model constant,qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffik p ¼ 1=3 þ 2c 2 c: Damage is assumed to start growing right at the onset of yielding, and sothe variable k d is identical with k p : The damage law has again the exponential form (14).In the first example, the plastic part of the model is designed to be perfectly plastic with aconstant yield stress in shear s y ¼ s 0 : The parameters are Young’s modulus E ¼ 30 GPa;Poisson’s ratio n ¼ 0:2; s 0 ¼ 20 MPa; c f ¼ 0:1; c c ¼ 0:05; e f ¼ 0:0057 and R ¼ 100 mm:The load–displacement curves for the three meshes from Figure 3 are almost the same; seeFigure 4. The evolution of the increment of the cumulative plastic strain k p is shown in Figure 5.The plastic zone initially has a certain width and later is reduced to a single element layer. Thisbehaviour is explained by the evolution of the critical plastic hardening modulus H crit;p : Theexpression for H crit;p has been derived analytically by Runesson et al. [33] and can be written forthe present case according to Rolshoven [34] as2! 3 2EH crit;p ¼ 44k p ð1 nÞ 2ðc Sf c c Þ 2 3ð1 nÞ pffiffiffiffiþ c f þ c c5 ð18ÞJ 2where S 3 is the out-of-plane principal effective deviatoric stress. In Figure 6, the evolution ofH crit;p is compared to the hardening modulus for the loading path that corresponds to theconditions of Figure 3. At early stages of the loading process, H crit;p is below H p ¼ 0; and so theplastic zone remains distributed. During plastic flow the out-of-plane effective stress componentincreases, which results in an increase of H crit;p : Eventually, H crit;p becomes positive, which leadsto a fully localized plastic zone. The evaluation of the critical plastic hardening modulus in (18)is based on the analysis of a bifurcation from a uniform state. Nevertheless, this idealized2.52mediumfinevery finenormalized load1.510.500 0.001 0.002 0.003normalized top displacementFigure 4. Load–displacement diagram for a panel loaded in compression under plane strain obtained withthe non-local damage-plastic model with H p ¼ 0; m ¼ 1 and R ¼ 0:1 m on three different meshes.Copyright # 2005 John Wiley & Sons, Ltd. Int. J. Numer. Anal. Meth. Geomech. 2006; 30:71–90
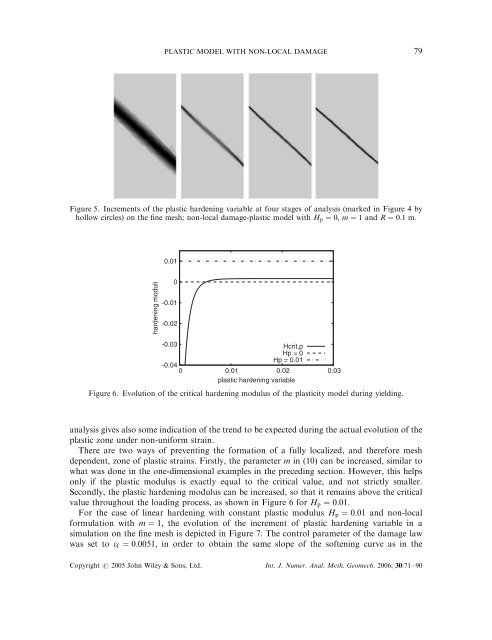
PLASTIC MODEL WITH NON-LOCAL DAMAGE 79Figure 5. Increments of the plastic hardening variable at four stages of analysis (marked in Figure 4 byhollow circles) on the fine mesh; non-local damage-plastic model with H p ¼ 0; m ¼ 1 and R ¼ 0:1 m:0.01hardening moduli0-0.01-0.02-0.03Hcrit,pHp = 0Hp = 0.01-0.040 0.01 0.02 0.03plastic hardening variableFigure 6. Evolution of the critical hardening modulus of the plasticity model during yielding.analysis gives also some indication of the trend to be expected during the actual evolution of theplastic zone under non-uniform strain.There are two ways of preventing the formation of a fully localized, and therefore meshdependent, zone of plastic strains. Firstly, the parameter m in (10) can be increased, similar towhat was done in the one-dimensional examples in the preceding section. However, this helpsonly if the plastic modulus is exactly equal to the critical value, and not strictly smaller.Secondly, the plastic hardening modulus can be increased, so that it remains above the criticalvalue throughout the loading process, as shown in Figure 6 for H p ¼ 0:01:For the case of linear hardening with constant plastic modulus H p ¼ 0:01 and non-localformulation with m ¼ 1; the evolution of the increment of plastic hardening variable in asimulation on the fine mesh is depicted in Figure 7. The control parameter of the damage lawwas set to e f ¼ 0:0051; in order to obtain the same slope of the softening curve as in theCopyright # 2005 John Wiley & Sons, Ltd. Int. J. Numer. Anal. Meth. Geomech. 2006; 30:71–90
Page 1 and 2: INTERNATIONAL JOURNAL FOR NUMERICAL
Page 3 and 4: PLASTIC MODEL WITH NON-LOCAL DAMAGE
Page 7: PLASTIC MODEL WITH NON-LOCAL DAMAGE

Plastic model with non-local damage applied to concrete

Create successful ePaper yourself

Delete template?

Save as template?