- Page 2:
Fuzzy Logic and Probability Applica
- Page 6:
Fuzzy Logic and Probability Applica
- Page 10:
To the memory of our colleague and
- Page 14:
Contents Foreword Lotfi A. Zadeh Fo
- Page 18:
Contents ix 5.1.1 A historical pers
- Page 22:
Contents xi 10.2.6 How can we solve
- Page 26:
Contents xiii 13.4.5 Summary 338 13
- Page 30:
Foreword Probability theory and fuz
- Page 34:
Lotfi A. Zadeh xvii event, if epsil
- Page 38:
Foreword Writing this foreword afte
- Page 42:
Preface This book is designed as a
- Page 46:
Acknowledgments Special thanks to t
- Page 50:
Parti Fundamentals JaneM. Booker 1.
- Page 54:
Chapter 1 Introduction Timothy J. R
- Page 58:
Timothy J. Ross, Jane M. Booker, an
- Page 62:
Timothy J. Ross, Jane M. Booker, an
- Page 66:
Timothy j. Ross, Jane M. Booker, an
- Page 70:
Timothy J. Ross, Jane M. Booker, an
- Page 74:
Timothy J. Ross, Jane M. Booker, an
- Page 78:
Timothy J. Ross, Jane M. Booker, an
- Page 82:
Timothy J. Ross, Jane M. Booker, an
- Page 86:
Timothy J. Ross, Jane M. Booker, an
- Page 90:
Timothy J. Ross, Jane M. Booker, an
- Page 94:
Timothy J. Ross, Jane M. Booker, an
- Page 98:
Timothy J. Ross, Jane M. Booker, an
- Page 102:
Timothy J. Ross, Jane M. Booker, an
- Page 106:
Chapter 2 Fuzzy Set Theory, Fuzzy L
- Page 110:
Timothy J. Ross and W. Jerry Parkin
- Page 114:
Timothy J. Ross and W. Jerry Parkin
- Page 118:
Timothy J. Ross and W. Jerry Parkin
- Page 122:
Timothy J. Ross and W. Jerry Parkin
- Page 126:
Timothy J. Ross and W. Jerry Parkin
- Page 130:
Timothy J. Ross and W. Jerry Parkin
- Page 134:
Timothy J. Ross and W. Jerry Parkin
- Page 138:
Timothy J. Ross and W. Jerry Parkin
- Page 142:
Timothy J. Ross and W. Jerry Parkin
- Page 146:
Timothy J. Ross and W. Jerry Parkin
- Page 150:
Timothy J. Ross and W. Jerry Parkin
- Page 154:
Timothy J. Ross and W. Jerry Parkin
- Page 158:
Chapter 3 Probability Theory Nozer
- Page 162:
Nozer D. Singpurwalla, Jane M. Book
- Page 166:
Nozer D. Singpurwalla, Jane M. Book
- Page 170:
Nozer D. Singpurwalla, Jane M. Book
- Page 174:
Nozer D. Singpurwalla, Jane M. Book
- Page 178:
Nozer D. Singpurwalla, Jane M. Book
- Page 182:
Nozer D. Singpurwalla, Jane M. Book
- Page 186:
Nozer D. Singpurwalla, Jane M. Book
- Page 190:
Nozer D. Singpurwalla, Jane M. Book
- Page 194: Chapter 4 Bayesiart Methods Kiflibe
- Page 198: Kimberly F. Sellers and Jane M. Boo
- Page 202: 5.3* HIGHER ORDER APPROXIMATIONS 24
- Page 206: Kimberly F. Sellers and Jane M. Boo
- Page 210: Kimberly F. Sellers and Jane M. Boo
- Page 214: Kimberly F. Sellers and Jane M. Boo
- Page 218: Kimberly F. Sellers and Jane M. Boo
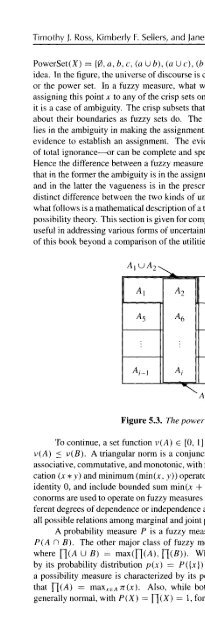
- Page 222: Chapter 5 Considerations for Using
- Page 226: Timothy ]. Ross, Kimberly F. Seller
- Page 230: Timothy J. Ross, Kimberly F. Seller
- Page 234: Timothy J. Ross, Kimberly F. Seller
- Page 238: Timothy J. Ross, Kimberly F. Seller
- Page 242: Timothy J. Ross, Kimberly F. Seller
- Page 248: 100 Chapter 5. Considerations for U
- Page 252: 102 Chapter 5. Considerations for U
- Page 256: 104 Chapter 5. Considerations for U
- Page 260: 106 Chapter 6. Guidelines for Elici
- Page 264: 108 Chapter 6. Guidelines for Elici
- Page 268: 110 Chapter 6. Guidelines for Elici
- Page 272: 112 Chapter 6. Guidelines for Elici
- Page 276: 114 Chapter 6. Guidelines for Elici
- Page 280: 116 Chapter 6. Guidelines for Elici
- Page 284: 118 Chapter 6. Guidelines for Elici
- Page 288: 120 Chapter 6. Guidelines for Elici
- Page 292: 122 Chapter 6. Guidelines for Elici
- Page 296:
This page intentionally left blank
- Page 300:
This page intentionally left blank
- Page 304:
128 Chapter 7. Image Enhancement: P
- Page 308:
130 Chapter 7. Image Enhancement: P
- Page 312:
132 Chapter 7. Image Enhancement: P
- Page 316:
134 Chapter 7. Image Enhancement: P
- Page 320:
136 Chapter 7. Image Enhancement: P
- Page 324:
138 Chapter 7. Image Enhancement: P
- Page 328:
140 Chapter 7. Image Enhancement: P
- Page 332:
142 Chapter 7. Image Enhancement: P
- Page 336:
144 Chapter 7. Image Enhancement: P
- Page 340:
146 Chapter 8. Engineering Process
- Page 344:
148 Chapter 8. Engineering Process
- Page 348:
150 Chapters. Engineering Process C
- Page 352:
152 Chapters. Engineering Process C
- Page 356:
154 Chapter 8. Engineering Process
- Page 360:
156 Chapter 8. Engineering Process
- Page 364:
158 Chapter 8. Engineering Process
- Page 368:
160 Chapter 8. Engineering Process
- Page 372:
162 Chapter 8. Engineering Process
- Page 376:
164 Chapter 8. Engineering Process
- Page 380:
166 Chapter 8. Engineering Process
- Page 384:
168 Chapter 8. Engineering Process
- Page 388:
1 70 Chapter 8. Engineering Process
- Page 392:
172 Chapter 8. Engineering Process
- Page 396:
1 74 Chapter 8. Engineering Process
- Page 400:
176 Chapter 8. Engineering Process
- Page 404:
178 Chapter 8. Engineering Process
- Page 408:
180 Chapter 8. Engineering Process
- Page 412:
182 Chapter 8. Engineering Process
- Page 416:
184 Chapter 8. Engineering Process
- Page 420:
186 Chapter 8. Engineering Process
- Page 424:
188 Chapter 8. Engineering Process
- Page 428:
190 Chapters. Engineering Process C
- Page 432:
This page intentionally left blank
- Page 436:
194 Chapter 9. Structural Safety An
- Page 440:
196 Chapter 9. Structural Safety An
- Page 444:
198 Chapter 9. Structural Safety An
- Page 448:
200 Chapter 9. Structural Safety An
- Page 452:
202 Chapter 9. Structural Safety An
- Page 456:
204 Chapter 9. Structural Safety An
- Page 460:
206 Chapter 9. Structural Safety An
- Page 464:
208 Chapter 9. Structural Safety An
- Page 468:
210 Chapter 9. Structural Safety An
- Page 472:
212 Chapter 9. Structural Safety An
- Page 476:
214 Chapter 9. Structural Safety An
- Page 480:
216 Chapter 9. Structural Safety An
- Page 484:
218 Chapter 9. Structural Safety An
- Page 488:
220 Chapter 10. Aircraft Integrity
- Page 492:
222 Chapter 10. Aircraft Integrity
- Page 496:
224 Chapter 10. Aircraft Integrity
- Page 500:
226 Chapter 10. Aircraft Integrity
- Page 504:
228 Chapter 10. Aircraft Integrity
- Page 508:
230 Chapter 10. Aircraft Integrity
- Page 512:
232 Chapter 10. Aircraft Integrity
- Page 516:
234 Chapter 10. Aircraft Integrity
- Page 520:
236 Chapter 10. Aircraft Integrity
- Page 524:
238 Chapter 10. Aircraft Integrity
- Page 528:
240 Chapter 10. Aircraft Integrity
- Page 532:
242 Chapter 10. Aircraft Integrity
- Page 536:
244 Chapter 11. Auto Reliability Pr
- Page 540:
246 Chapter 11. Auto Reliability Pr
- Page 544:
248 Chapter 11. Auto Reliability Pr
- Page 548:
250 Chapter 11. Auto Reliability Pr
- Page 552:
252 Chapter 11. Auto Reliability Pr
- Page 556:
254 Chapter 11. Auto Reliability Pr
- Page 560:
256 Chapter 11. Auto Reliability Pr
- Page 564:
258 Chapter 11. Auto Reliability Pr
- Page 568:
260 Chapter 11. Auto Reliability Pr
- Page 572:
This page intentionally left blank
- Page 576:
264 Chapter 12. Control Charts for
- Page 580:
266 Chapter 12. Control Charts for
- Page 584:
268 Chapter 12. Control Charts for
- Page 588:
270 Chapter 12. Control Charts for
- Page 592:
272 Chapter 12. Control Charts for
- Page 596:
274 Chapter 12. Control Charts for
- Page 600:
276 Chapter 12. Control Charts for
- Page 604:
278 Chapter 12. Control Charts for
- Page 608:
280 Chapter 12. Control Charts for
- Page 612:
282 Chapter 12. Control Charts for
- Page 616:
284 Chapter 12. Control Charts for
- Page 620:
286 Chapter 12. Control Charts for
- Page 624:
288 Chapter 12. Control Charts for
- Page 628:
290 Chapter 12. Control Charts for
- Page 632:
292 Chapter 12. Control Charts for
- Page 636:
294 Chapter 12. Control Charts for
- Page 640:
296 Chapter 12. Control Charts for
- Page 644:
298 Chapter 12. Control Charts for
- Page 648:
300 Chapter 12. Control Charts for
- Page 652:
302 Chapter 12. Control Charts for
- Page 656:
304 Chapter 12. Control Charts for
- Page 660:
306 Chapter 12. Control Charts for
- Page 664:
308 Chapter 12. Control Charts for
- Page 668:
310 Chapter 1 2. Control Charts for
- Page 672:
312 Chapter 12. Control Charts for
- Page 676:
314 Chapter 12. Control Charts for
- Page 680:
316 Chapter 12. Control Charts for
- Page 684:
318 Chapter 12. Control Charts for
- Page 688:
320 Chapter 12. Control Charts for
- Page 692:
322 Chapter 12. Control Charts for
- Page 696:
This page intentionally left blank
- Page 700:
326 Chapter 13. Fault Tree Logic Mo
- Page 704:
328 Chapter 13. Fault Tree Logic Mo
- Page 708:
330 Chapter 13. Fault Tree Logic Mo
- Page 712:
332 Chapter 13. Fault Tree Logic Mo
- Page 716:
334 Chapter 13. Fault Tree Logic Mo
- Page 720:
336 Chapter 13. Fault Tree Logic Mo
- Page 724:
338 Chapter 13. Fault Tree Logic Mo
- Page 728:
340 Chapter 13. Fault Tree Logic Mo
- Page 732:
342 Chapter 13. Fault Tree Logic Mo
- Page 736:
344 Chapter 13. Fault Tree Logic Mo
- Page 740:
346 Chapter 13. Fault Tree Logic Mo
- Page 744:
348 Chapter 14. Uncertainty Distrib
- Page 748:
350 Chapter 14. Uncertainty Distrib
- Page 752:
352 Chapter 14. Uncertainty Distrib
- Page 756:
354 Chapter 14. Uncertainty Distrib
- Page 760:
356 Chapter 14. Uncertainty Distrib
- Page 764:
358 Chapter 14. Uncertainty Distrib
- Page 768:
360 Chapter 14. Uncertainty Distrib
- Page 772:
362 Chapter 14. Uncertainty Distrib
- Page 776:
364 Chapter 14. Uncertainty Distrib
- Page 780:
366 Chapter 1 5. Signal Validation
- Page 784:
368 Chapter 15. Signal Validation U
- Page 788:
370 Chapter 1 5. Signal Validation
- Page 792:
372 Chapter 15. Signal Validation U
- Page 796:
374 Chapter 1 5. Signal Validation
- Page 800:
376 Chapter 1 5. Signal Validation
- Page 804:
378 Chapter 1 5. Signal Validation
- Page 808:
380 Chapter 15. Signal Validation U
- Page 812:
382 Chapter 15. Signal Validation U
- Page 816:
384 Chapter 15. Signal Validation U
- Page 820:
386 Chapter 15. Signal Validation U
- Page 824:
388 Chapter 15. Signal Validation U
- Page 828:
390 Chapter 15. Signal Validation U
- Page 832:
392 Chapter 15. Signal Validation U
- Page 836:
394 Index logic, 90 membership, 30
- Page 840:
396 Index fuzzy, 150-152, 157, 160,
- Page 844:
398 Index Dempster-Shafer, 8 exclud
- Page 848:
400 Index hard data, 68 hardware re
- Page 852:
402 Index of probability, 57 union,
- Page 856:
404 Index plausibility, 101 polemic
- Page 860:
406 Index definition of probability
- Page 864:
408 Index cutting, 349-352 wear, 34