Rencontre du Non-Linéaire

Synchronisation de systèmes chaotiques bidirectionnellement couplés 77
En regard de la remarque 5 précédente et afin de s’affranchir partiellement de la dépendance de
l’expression de ˙V vis à vis de certains états, posons, par exemple, p 13 = 0 et p 23 = 0. Ceci conduit alors
à l’expression simplifiée :
dV
dt = (2K xp 11 +p 12 )e 2 x +[(2(K x +K y )+a)p 12 −p 11 +p 22 ]e y e x +((z 1 −e z )p 33 −p 11 )e z e x
+((a+2K y )p 22 −p 12 )e 2 y +(−p 12)e z e y +((2K z +x 1 −c)p 33 )e 2 z . (13)
Afin de garantirla négativitéde dV
dt
, il est naturelde chercher,autraversdes termes de commande(ici,
ununiqueterme),àinfluersurlestermesquadratiquesde(13):seulstermespourlesquelsilestpossiblede
garantir le signe. Néanmoins, fondamentalement, trois cas sont envisageables : {K x ≠ 0,K y = K z = 0},
{K y ≠ 0,K x = K z = 0}, {K z ≠ 0,K x = K y = 0}. Intéressons-nous arbitrairement (sans perte toutefois
de généralité) au second cas, qui conduit alors à définir la dérivée de la fonction de Lyapunov comme
suit :
dV
dt = p 12e 2 x +[(2K y +a)p 12 −p 11 +p 22 ]e y e x +[(z 1 −e z )p 33 −p 11 ]e z e x
+[(a+2K y )p 22 −p 12 ]e 2 y +(−p 12 )e z e y +[(x 1 −c)p 33 ]e 2 (14)
z
Remarque 6. Le terme quadratique p 12 e 2 x peut être rendu négatif en optant pour p 12 < 0 (inégalité
compatible avec la remarque 4). Sachant que a et p 22 sont positifs et p 12 < 0, le terme quadratique
[(a+2K y )p 22 −p 12 ]e 2 y peut également être rendu négatif par une sélection appropriéedu gain K y tel que :
K y < 1 2
( )
p12
−a
p 22
(avec p 22 > 0 et p 12 < 0). (15)
Enrevanche,il n’existeaucunegarantie(ni d’interventionpossible)pourlanégativitéde[(x 1 −c)p 33 ]e 2 z
sachant que, d’après CS3 1 , p 33 > 0. Cela signifie que cette négativité est effective si c majore x 1 , ce qui
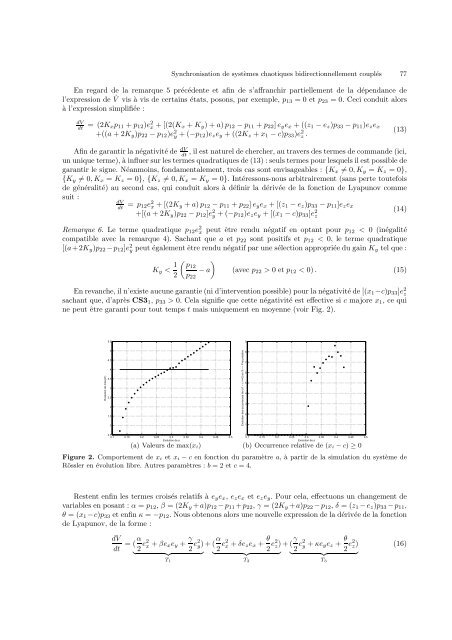
ne peut être garanti pour tout temps t mais uniquement en moyenne (voir Fig. 2).
5.5
9
Evolution de max(x1)
5
4.5
4
3.5
3
2.5
2
1.5
1
Evolution des occurrences de (x1 − c >=0) en % −− Freq relative
8
7
6
5
4
3
2
1
0.5
0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
Evolution de a
(a) Valeurs de max(x i)
0
0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
Evolution de a
(b) Occurrence relative de (x i −c) ≥ 0
Figure 2. Comportement de x i et x i − c en fonction du paramètre a, à partir de la simulation du système de
Rössler en évolution libre. Autres paramètres : b = 2 et c = 4.
Restent enfin les termes croisés relatifs à e y e x , e z e x et e z e y . Pour cela, effectuons un changement de
variables en posant : α = p 12 , β = (2K y +a)p 12 −p 11 +p 22 , γ = (2K y +a)p 22 −p 12 , δ = (z 1 −e z )p 33 −p 11 ,
θ = (x 1 −c)p 33 et enfin κ = −p 12 . Nous obtenons alorsune nouvelle expressionde la dérivéede la fonction
de Lyapunov, de la forme :
dV
dt = (α 2 e2 x +βe x e y + γ 2 e2 y) +( α
} {{ }
2 e2 x +δe z e x + θ 2 e2 z) +( γ
} {{ }
2 e2 y +κe y e z + θ 2 e2 z) (16)
} {{ }
T 1 T 2 T 3