nL;

8120
By the statement of the problem,
the two odd numbers in question are
different-otherwise, their product
wouldbe equal to the square of their
half-sum. So the smallest possible
product is 1 1 . 13 : l43j the next one
is 11 . 15 = 165. Since there are no
pyramids as high as 165 m, the nuinbers
are I I and 13, and the height of
the pyramid is greater than 143 m
but less than [(11 + L3ll2l2:144rr,.
There are two pyramids in Egypt
higher than 143 m: the pyramid of
Khufu (Cheops) at 146.6 m and that
of Khafre (Chephren) at 143.5 m. So
the pyramid was built for Chephren.
Iilings
l. For figure 3a in the article the
answer is I llmn+ 1); forfigure 3b it's
I llmn - 1). In both cases the answer
is obtained by extending the grid of
the small parallelograms and counting
nodes inside the big parallelogram.
2.It canbe proved that the points
A, B, C and the intersection points
of AA' BBr, ar,dCCrcanbe considered
nodes of a parallelogram grid
(fig. 12). Then the arca of ABC
equals 3 + 3' 116 = 3% times the
area of a grid parallelogram, while
the area of the small (shaded) triangle
is LlZ of this unit. So the answer
is ll2 + 3/, = /7 .
The existence of the parallelogram
grid in the solution above can
be derived, for example, from the
fact that the segments AA' BBr,
CC, divide each other in theiatio 3
:3 : 1. A proof is left to the reader.
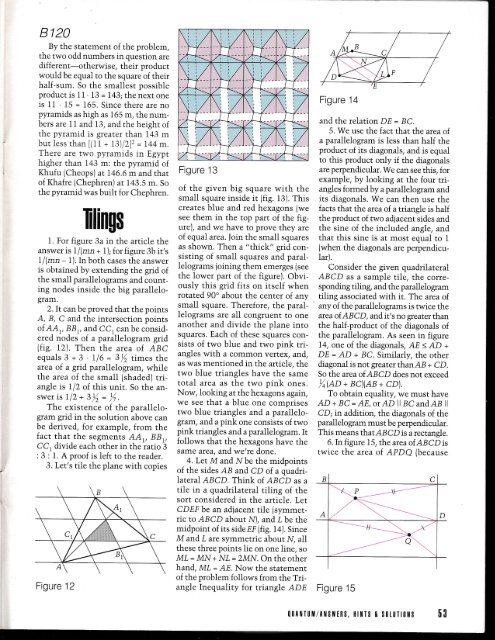
3. Let's tile the plane with copies
Figure 12
Figure 13
of the given big square with the
small square inside it (fig. 13). This
creates blue and red hexagons (we
see them in the top part of the figure),
and we have to prove they are
of equal area. |oin the small squares
as shown. Then a "thick" grid consisting
of small squares and parallelograms
joining them emerges (see
the lower part of the figure). Obviously
this grid fits on itself when
rotated 90' about the center of any
small square. Therefore, the paral-
Ielograms are all congruent to one
another and divide the plane into
squares. Each of these squares consists
of two blue and two pink triangles
with a common vertex, and,
as was mentioned in the article, the
two blue triangies have the same
total area as the two pink ones.
Now, looking at the hexagons again,
we see that a blue one comprises
two blue triangles and a parallelogram,
and a pink one consists of two
pink triangles and a parallelogram. It
follows that the hexagons have the
same areal and we're done.
4.Let M and Nbe the midpoints
of the sides AB and CD of a quadrilateral
ABCD. Think of ABCD as a
tile in a quadrilateral tiling of the
sort considered in the article. Let
CDEF be an adjacent tile (symmetric
to ABCD about N), and I be the
midpoint of its side EF (fig. 14). Since
M andl are symmetric about N, all
these three points lie on one line, so
ML = MN + NL:zMN. On the other
hand, ML = AE. Now the statement
of the problem follows from the Triangle
Inequality for ttiangle ADE
Figure 14
and the relation DE = BC.
5. We use the fact that the area ot
a parallelogram is less than half the
product of its diagonals, and is equal
to this product only if the diagonals
are perpendicular. We can see this, for
example, by looking at the four triangles
formed by a parallelogram and
its diagonals. We can then use the
facts that the area of a triangle is half
the product of two adjacent sides and
the sine of the included angle, and
that this sine is at most equal to I
(when the diagonals are perpendicular).
Consider the given quadrilateral
ABCD as a sample tile, the corresponding
tiiing and the paralleiogram
tiling associated with it. The area of
any of the parallelograms is twice the
areaof.ABCD, and it's no greater than
the half-product of the diagonals of
the parallelogram. As seen in figure
14, one of the diagonals, AE a AD +
DE = AD + BC. Similarly, the other
diagonal is not greater thanAB + CD.
So the areaof ABCD does not exceed
%Ao+BCI(AB+cDl.
To obtain equality, we must have
AD + BC = AE, or AD ll BC andAB ll
CDi in addition, the diagonals of the
parallelogram must be perpenficular.
This means that AB CD is a rectangle.
6.Infigure 15, the areaof ABCDis
twice the area of APDQ (because
\--->
Figure 15
0uAr/TUlll/ilJSIttRS, tltirrS & S0t lJil0ils 53