PDF (361 K) - Laboratoire Matière et Systèmes Complexes - Paris 7

Fig. 5 Calculated shapes of the vesicle inside the cylindrical nanochannel
in a symmetry plane (x,z). Top: G ¼ 0 (no adhesion) for the
reduced tensions s ¼ 0, s ¼ 10, s ¼ 1 10 2 , s ¼ 1 10 3 , s ¼ 1 10 5 (from
top to bottom). Bottom: G ¼ 2 for the same reduced tensions, however
from bottom to top. In both cases, for s ¼ 1 10 5 the shape is almost
a half-sphere.
tension increases, the vesicle tends to a sphere of radius equal to
the radius of the channel—except within a small region of size
xO(k/s) close the channel walls.
The deviation of the shape from a spherical cap of radius
equal to the radius of the channel can be characterized by the
normalized height h ¼ z(r ¼ 0)/a of the top of the vesicle with
respect to the detachment point (see Fig. 6). Increasing the
adhesion energy at fixed tension reduces the height of the
vesicle. When the adhesion energy G equals k/(2a 2 )(G ¼ 1/2),
the vesicle becomes exactly a half-sphere with radius equal to
the channel radius, whatever the tension. Indeed, according to
eqn (11), for G ¼ k/(2a 2 ) the curvature at the detachment point is
1/a and a perfect sphere is always a solution of the shape
equations. In this case, the pressure drop is related to the
tension by the ordinary Laplace law; indeed, the curvature
terms in eqn (2) vanish. At adhesion energies higher than k/(2a 2 )
(G > 1/2), the vesicle develops an oblate shape that tends to
a sphere as the tension increases (see Fig. 6 and bottom curves
of Fig. 5).
Fig. 6 The normalized height h of the top of the vesicle (with respect to
the detachment point) in the cylindrical nanochannel, as a function of the
reduced tension s for different normalized adhesion energies G (G ¼ 0, G
¼ 0.2, G ¼ 0.5, G ¼ 2, G ¼ 10). For G ¼ 1/2, the vesicle is a perfect halfsphere
of radius a whatever the tension.
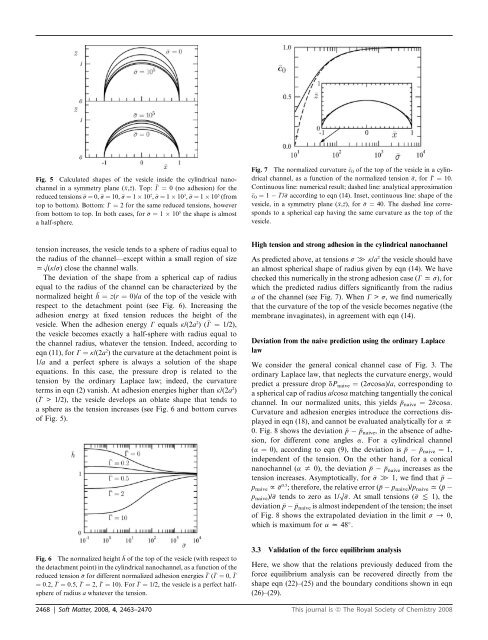
Fig. 7 The normalized curvature c 0 of the top of the vesicle in a cylindrical
channel, as a function of the normalized tension s, for G ¼ 10.
Continuous line: numerical result; dashed line: analytical approximation
c0 ¼ 1 G/s according to eqn (14). Inset, continuous line: shape of the
vesicle, in a symmetry plane (x,z), for s ¼ 40. The dashed line corresponds
to a spherical cap having the same curvature as the top of the
vesicle.
High tension and strong adhesion in the cylindrical nanochannel
As predicted above, at tensions s [ k/a 2 the vesicle should have
an almost spherical shape of radius given by eqn (14). We have
checked this numerically in the strong adhesion case (G x s), for
which the predicted radius differs significantly from the radius
a of the channel (see Fig. 7). When G > s, we find numerically
that the curvature of the top of the vesicle becomes negative (the
membrane invaginates), in agreement with eqn (14).
Deviation from the naive prediction using the ordinary Laplace
law
We consider the general conical channel case of Fig. 3. The
ordinary Laplace law, that neglects the curvature energy, would
predict a pressure drop dPnaive ¼ (2scosa)/a, corresponding to
a spherical cap of radius a/cosa matching tangentially the conical
channel. In our normalized units, this yields pnaive ¼ 2scosa.
Curvature and adhesion energies introduce the corrections displayed
in eqn (18), and cannot be evaluated analytically for a s
0. Fig. 8 shows the deviation p p naive, in the absence of adhesion,
for different cone angles a. For a cylindrical channel
(a ¼ 0), according to eqn (9), the deviation is p p naive ¼ 1,
independent of the tension. On the other hand, for a conical
nanochannel (a s 0), the deviation p pnaive increases as the
tension increases. Asymptotically, for s [ 1, we find that p
pnaive f s 0.5 ; therefore, the relative error (p pnaive)/pnaive x (p
pnaive)/s tends to zero as 1/Os. At small tensions (s ( 1), the
deviation p pnaive is almost independent of the tension; the inset
of Fig. 8 shows the extrapolated deviation in the limit s / 0,
which is maximum for a x 48 .
3.3 Validation of the force equilibrium analysis
Here, we show that the relations previously deduced from the
force equilibrium analysis can be recovered directly from the
shape eqn (22)–(25) and the boundary conditions shown in eqn
(26)–(29).
2468 | Soft Matter, 2008, 4, 2463–2470 This journal is ª The Royal Society of Chemistry 2008