- Page 1 and 2:
First Semester in Numerical Analysi
- Page 3 and 4:
First Semester in Numerical Analysi
- Page 5 and 6:
Contents 1 Introduction 5 1.1 Revie
- Page 7 and 8:
Preface This book is based on my le
- Page 9 and 10:
Chapter 1 Introduction 1.1 Review o
- Page 11 and 12:
CHAPTER 1. INTRODUCTION 8 Solution.
- Page 13 and 14:
CHAPTER 1. INTRODUCTION 10 Let’s
- Page 15 and 16:
CHAPTER 1. INTRODUCTION 12 Out[8]:
- Page 17 and 18:
CHAPTER 1. INTRODUCTION 14 Press ]
- Page 19 and 20:
CHAPTER 1. INTRODUCTION 16 Matrix o
- Page 21 and 22:
CHAPTER 1. INTRODUCTION 18 stdlib/v
- Page 23 and 24:
CHAPTER 1. INTRODUCTION 20 In [37]:
- Page 25 and 26:
CHAPTER 1. INTRODUCTION 22 In [48]:
- Page 27 and 28:
CHAPTER 1. INTRODUCTION 24 -0.62988
- Page 29 and 30:
CHAPTER 1. INTRODUCTION 26 5 7 9 He
- Page 31 and 32:
CHAPTER 1. INTRODUCTION 28 Sometime
- Page 33 and 34:
CHAPTER 1. INTRODUCTION 30 where s
- Page 35 and 36:
CHAPTER 1. INTRODUCTION 32 Notice t
- Page 37 and 38:
CHAPTER 1. INTRODUCTION 34 and real
- Page 39 and 40:
CHAPTER 1. INTRODUCTION 36 In [4]:
- Page 41 and 42:
CHAPTER 1. INTRODUCTION 38 Chopping
- Page 43 and 44:
CHAPTER 1. INTRODUCTION 40 Machine
- Page 45 and 46:
CHAPTER 1. INTRODUCTION 42 The abso
- Page 47 and 48:
CHAPTER 1. INTRODUCTION 44 Next wil
- Page 49 and 50:
CHAPTER 1. INTRODUCTION 46 In [1]:
- Page 51 and 52:
CHAPTER 1. INTRODUCTION 48 Exercise
- Page 53 and 54:
CHAPTER 1. INTRODUCTION 50 Sources
- Page 55 and 56:
CHAPTER 2. SOLUTIONS OF EQUATIONS:
- Page 57 and 58:
CHAPTER 2. SOLUTIONS OF EQUATIONS:
- Page 59 and 60:
CHAPTER 2. SOLUTIONS OF EQUATIONS:
- Page 61 and 62:
CHAPTER 2. SOLUTIONS OF EQUATIONS:
- Page 63 and 64:
CHAPTER 2. SOLUTIONS OF EQUATIONS:
- Page 65 and 66:
CHAPTER 2. SOLUTIONS OF EQUATIONS:
- Page 67 and 68:
CHAPTER 2. SOLUTIONS OF EQUATIONS:
- Page 69 and 70:
CHAPTER 2. SOLUTIONS OF EQUATIONS:
- Page 71 and 72:
CHAPTER 2. SOLUTIONS OF EQUATIONS:
- Page 73 and 74:
CHAPTER 2. SOLUTIONS OF EQUATIONS:
- Page 75 and 76:
CHAPTER 2. SOLUTIONS OF EQUATIONS:
- Page 77 and 78:
CHAPTER 2. SOLUTIONS OF EQUATIONS:
- Page 79 and 80:
CHAPTER 2. SOLUTIONS OF EQUATIONS:
- Page 81 and 82:
CHAPTER 2. SOLUTIONS OF EQUATIONS:
- Page 83 and 84:
CHAPTER 2. SOLUTIONS OF EQUATIONS:
- Page 85 and 86:
CHAPTER 2. SOLUTIONS OF EQUATIONS:
- Page 87 and 88:
CHAPTER 2. SOLUTIONS OF EQUATIONS:
- Page 89 and 90:
CHAPTER 2. SOLUTIONS OF EQUATIONS:
- Page 91 and 92:
Chapter 3 Interpolation In this cha
- Page 93 and 94:
CHAPTER 3. INTERPOLATION 90 Here is
- Page 95 and 96:
CHAPTER 3. INTERPOLATION 92 basis f
- Page 97 and 98:
CHAPTER 3. INTERPOLATION 94 therefo
- Page 99 and 100:
CHAPTER 3. INTERPOLATION 96 Summary
- Page 101 and 102:
CHAPTER 3. INTERPOLATION 98 and thu
- Page 103 and 104:
CHAPTER 3. INTERPOLATION 100 With t
- Page 105 and 106:
CHAPTER 3. INTERPOLATION 102 Exampl
- Page 107 and 108:
CHAPTER 3. INTERPOLATION 104 Exerci
- Page 109 and 110:
CHAPTER 3. INTERPOLATION 106 end en
- Page 111 and 112:
CHAPTER 3. INTERPOLATION 108 increa
- Page 113 and 114:
CHAPTER 3. INTERPOLATION 110 The ne
- Page 115 and 116:
CHAPTER 3. INTERPOLATION 112 there
- Page 117 and 118:
CHAPTER 3. INTERPOLATION 114 Figure
- Page 119 and 120:
CHAPTER 3. INTERPOLATION 116 Then t
- Page 121 and 122:
CHAPTER 3. INTERPOLATION 118 end en
- Page 123 and 124:
CHAPTER 3. INTERPOLATION 120 Exerci
- Page 125 and 126:
CHAPTER 3. INTERPOLATION 122 yi yi+
- Page 127 and 128:
CHAPTER 3. INTERPOLATION 124 • Cl
- Page 129 and 130:
CHAPTER 3. INTERPOLATION 126 In [2]
- Page 131 and 132:
CHAPTER 3. INTERPOLATION 128 end fo
- Page 133 and 134:
CHAPTER 3. INTERPOLATION 130 end en
- Page 135 and 136:
CHAPTER 3. INTERPOLATION 132 end u=
- Page 137 and 138:
CHAPTER 3. INTERPOLATION 134 Especi
- Page 139 and 140:
CHAPTER 3. INTERPOLATION 136 Arya a
- Page 141 and 142:
CHAPTER 3. INTERPOLATION 138 This l
- Page 143 and 144:
CHAPTER 3. INTERPOLATION 140 Recrea
- Page 145 and 146:
CHAPTER 4. NUMERICAL QUADRATURE AND
- Page 147 and 148:
CHAPTER 4. NUMERICAL QUADRATURE AND
- Page 149 and 150:
CHAPTER 4. NUMERICAL QUADRATURE AND
- Page 151 and 152:
CHAPTER 4. NUMERICAL QUADRATURE AND
- Page 153 and 154:
CHAPTER 4. NUMERICAL QUADRATURE AND
- Page 155 and 156:
CHAPTER 4. NUMERICAL QUADRATURE AND
- Page 157 and 158:
CHAPTER 4. NUMERICAL QUADRATURE AND
- Page 159 and 160:
CHAPTER 4. NUMERICAL QUADRATURE AND
- Page 161 and 162:
CHAPTER 4. NUMERICAL QUADRATURE AND
- Page 163 and 164:
CHAPTER 4. NUMERICAL QUADRATURE AND
- Page 165 and 166: CHAPTER 4. NUMERICAL QUADRATURE AND
- Page 167 and 168: CHAPTER 4. NUMERICAL QUADRATURE AND
- Page 169 and 170: CHAPTER 4. NUMERICAL QUADRATURE AND
- Page 171 and 172: CHAPTER 4. NUMERICAL QUADRATURE AND
- Page 173 and 174: CHAPTER 4. NUMERICAL QUADRATURE AND
- Page 175 and 176: CHAPTER 4. NUMERICAL QUADRATURE AND
- Page 177 and 178: CHAPTER 4. NUMERICAL QUADRATURE AND
- Page 179 and 180: CHAPTER 4. NUMERICAL QUADRATURE AND
- Page 181 and 182: Chapter 5 Approximation Theory 5.1
- Page 183 and 184: CHAPTER 5. APPROXIMATION THEORY 180
- Page 185 and 186: CHAPTER 5. APPROXIMATION THEORY 182
- Page 187 and 188: CHAPTER 5. APPROXIMATION THEORY 184
- Page 189 and 190: CHAPTER 5. APPROXIMATION THEORY 186
- Page 191 and 192: CHAPTER 5. APPROXIMATION THEORY 188
- Page 193 and 194: CHAPTER 5. APPROXIMATION THEORY 190
- Page 195 and 196: CHAPTER 5. APPROXIMATION THEORY 192
- Page 197 and 198: CHAPTER 5. APPROXIMATION THEORY 194
- Page 199 and 200: CHAPTER 5. APPROXIMATION THEORY 196
- Page 201 and 202: CHAPTER 5. APPROXIMATION THEORY 198
- Page 203 and 204: CHAPTER 5. APPROXIMATION THEORY 200
- Page 205 and 206: CHAPTER 5. APPROXIMATION THEORY 202
- Page 207 and 208: CHAPTER 5. APPROXIMATION THEORY 204
- Page 209 and 210: CHAPTER 5. APPROXIMATION THEORY 206
- Page 211 and 212: CHAPTER 5. APPROXIMATION THEORY 208
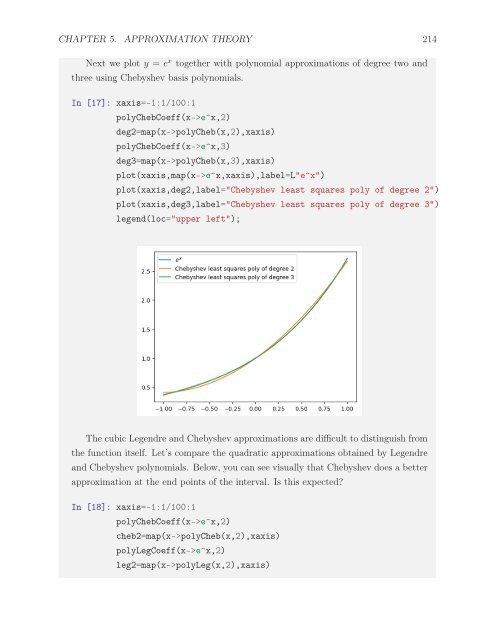
- Page 213 and 214: CHAPTER 5. APPROXIMATION THEORY 210
- Page 215: CHAPTER 5. APPROXIMATION THEORY 212
- Page 219 and 220: CHAPTER 5. APPROXIMATION THEORY 216
- Page 221 and 222: Index Absolute error, 38 Beasley-Sp
- Page 223 and 224: INDEX 220 Chebyshev, 203 Julia code