Yet Another Calculus Text, 2007a

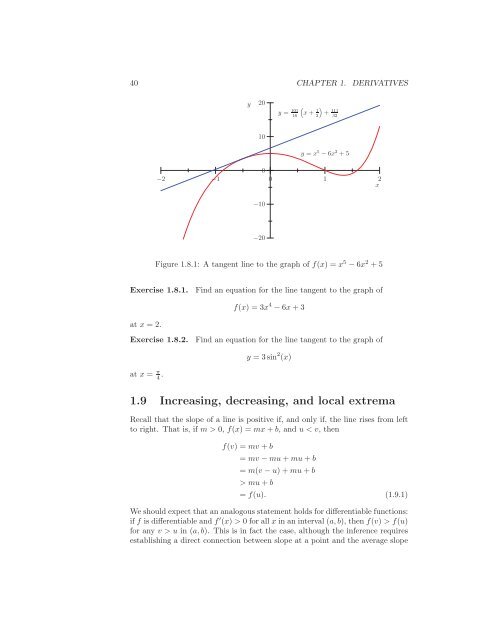
40 CHAPTER 1. DERIVATIVES
y
20
y = 101
16
( )
x +
1
2 +
111
32
10
y = x 5 − 6x 2 +5
0
−2 −1 0 1 2
x
−10
−20
Figure 1.8.1: A tangent line to the graph of f(x) =x 5 − 6x 2 +5
Exercise 1.8.1.
Find an equation for the line tangent to the graph of
f(x) =3x 4 − 6x +3
at x =2.
Exercise 1.8.2.
Find an equation for the line tangent to the graph of
y =3sin 2 (x)
at x = π 4 .
1.9 Increasing, decreasing, and local extrema
Recall that the slope of a line is positive if, and only if, the line rises from left
to right. That is, if m>0, f(x) =mx + b, andumu+ b
= f(u). (1.9.1)
We should expect that an analogous statement holds for differentiable functions:
if f is differentiable and f ′ (x) > 0 for all x in an interval (a, b), then f(v) >f(u)
for any v>uin (a, b). This is in fact the case, although the inference requires
establishing a direct connection between slope at a point and the average slope