3.4 The Point-Slope Form of a Line
3.4 The Point-Slope Form of a Line
3.4 The Point-Slope Form of a Line
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
296 Chapter 3 <strong>Line</strong>ar Functions<br />
Version: Fall 2007<br />
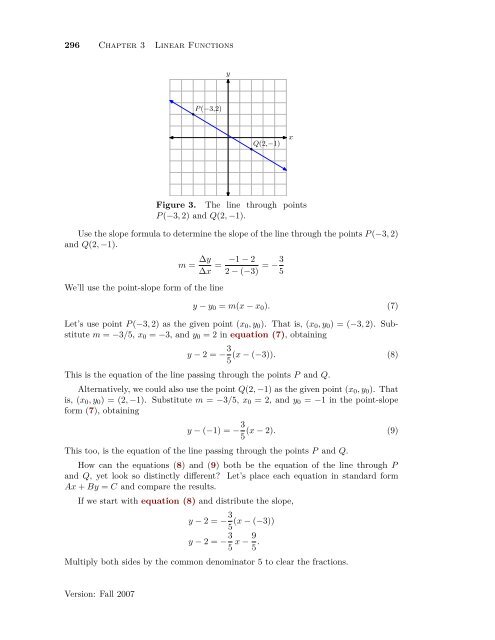
P (−3,2)<br />
y<br />
Q(2,−1)<br />
Figure 3. <strong>The</strong> line through points<br />
P (−3, 2) and Q(2, −1).<br />
Use the slope formula to determine the slope <strong>of</strong> the line through the points P (−3, 2)<br />
and Q(2, −1).<br />
We’ll use the point-slope form <strong>of</strong> the line<br />
m = ∆y −1 − 2<br />
= = −3<br />
∆x 2 − (−3) 5<br />
x<br />
y − y0 = m(x − x0). (7)<br />
Let’s use point P (−3, 2) as the given point (x0, y0). That is, (x0, y0) = (−3, 2). Substitute<br />
m = −3/5, x0 = −3, and y0 = 2 in equation (7), obtaining<br />
y − 2 = − 3<br />
(x − (−3)). (8)<br />
5<br />
This is the equation <strong>of</strong> the line passing through the points P and Q.<br />
Alternatively, we could also use the point Q(2, −1) as the given point (x0, y0). That<br />
is, (x0, y0) = (2, −1). Substitute m = −3/5, x0 = 2, and y0 = −1 in the point-slope<br />
form (7), obtaining<br />
y − (−1) = − 3<br />
(x − 2). (9)<br />
5<br />
This too, is the equation <strong>of</strong> the line passing through the points P and Q.<br />
How can the equations (8) and (9) both be the equation <strong>of</strong> the line through P<br />
and Q, yet look so distinctly different? Let’s place each equation in standard form<br />
Ax + By = C and compare the results.<br />
If we start with equation (8) and distribute the slope,<br />
y − 2 = − 3<br />
(x − (−3))<br />
5<br />
y − 2 = − 3 9<br />
x −<br />
5 5 .<br />
Multiply both sides by the common denominator 5 to clear the fractions.