Poly du TPMDP2 : Partie à préparer

tel que ¥ : ¥ 0 ¦¨§ ©
α 1.
&
ondulations pour t < −T et t > 6 7 8 9¨:; < =¨> =
<
T)
D
2 Préparation des T.P.
La fonction de transfert P(f) d'un filtre en “cosinus surélevé” est une fonction paire de f
avec pour f
⎧
1−
¢¡¤£ α
⎪
p( 0) ⋅ T pour f <
2T
⎪
⎪ p( 0)
⋅T
⎧ ⎛ π T ⎛ 1−α ⎞⎞⎫
1−α 1+ α
P( f ) = ⎨ ⋅ ⎨1+ cos⎜
⋅ ⎜ f − ⎟ pour f
α T
⎟⎬
< <
⎪ 2 ⎩ ⎝ ⎝ 2 ⎠⎠⎭
2T 2T
⎪ 1+ α
⎪ 0 pour < f
⎩ 2T
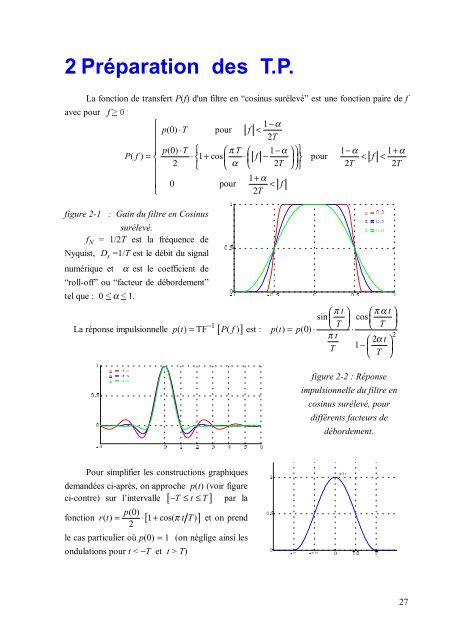
figure 2-1 : Gain du filtre en Cosinus
surélevé.
f N = 1/2T est la fréquence de
Nyquist, D s =1/T est le débit du signal
numérique et α est le coefficient de
“roll-off” ou “facteur de débordement”
−1
La réponse impulsionnelle p( t) TF [ P( f )]
= est :
⎛ π t ⎞ ⎛ π α t ⎞
sin ⎜ cos
T
⎟ ⎜
T
⎟
p( t) = p( 0)
⋅
⎝ ⎠
⋅
⎝ ⎠
π t
⎛ 2α t ⎞
2
T
1− ⎜ ⎟
⎝ T ⎠
'()
+,-./ *
+,-.0
12345
figure 2-2 : Réponse
impulsionnelle du filtre en
cosinus surélevé, pour
différents facteurs de
débordement.
! " # $ %
Pour simplifier les constructions graphiques
demandées ci-après, on approche p(t) (voir figure
−T ≤ t ≤ T par la
ci-contre) sur l’intervalle [ ]
p( 0)
2
fonction r( t) = ⋅[ 1+ cos( π t T)
]
et on prend
le cas particulier où p(0) = 1 (on néglige ainsi les
@BAC
EGF HGI
27

¢¡¤£
¥§¦©¨¦©
Considérons le schéma synoptique d' une modulation d' impulsion en amplitudes sur
fréquence porteuse :
Suite {b k }
b k ∈ {0,1}
débit 1/T
Codage
binaire
à M-aire
x(t)
Formant
Filtre
passebas
y(t) z(t)
Réponse impulsionnelle = r(t)
cos(2πf 0 t)
Nous avons dans le cas binaire ( M = 2 ) :
+∞
( ) ∑ k
avec la règle de codage
Le signal x t = a ⋅δ
( t − kT )
k=−∞
+∞
∑
Le signal y t = x t ∗ r t = a ⋅ r ( t − kT )
( ) ( ) ( ) k
k=−∞
Le signal π ⎜ ( )
⎧ak
= −1 si bk
= " 0"
⎨
⎩ak
= +1 si bk
= " 1"
⎛ +∞
⎞
z( t) = y( t) ⋅ cos( 2 f0 t) = ak
⋅ r t − kT ⋅ cos( 2π
f0
t)
⎜ ∑ avec f
⎟
0 >> 1 / T .
⎝ k=−∞
⎠
Question : Construire y(t) et z(t) pour la séquence binaire suivante :
T
Suite
Binaire {b k }
+1
x(t)
0 T
3T 4T 5T
7T
11T 12T 13T
−1
2T
6T
8T 9T 10T
28
Remarque 1 : pour la construction de y(t) et z(t), on négligera les phénomènes
− T < t < 0 et
transitoires de début et fin de séquence, c' est-à-dire les courbes situées entre [ ]
[ 13 T < t < 14 T ] en se référant à la graduation de l' axe des temps de x(t) (prendre T=1cm et
1cm pour la valeur unité en ordonnée).
Remarque 2 : pour la construction de z(t), comme f >> 1 / T , on se contentera de faire
figurer l’enveloppe de z(t) en précisant l' état de phase de la porteuse à l' intérieur de ces
extremums (voir l' exemple ci-dessous).
0

Signal modulant m(t)
Signal modulé m(t)·cos(2π f 0 t) .
En phase avec la porteuse
t
(0)
π
( ) (0)
π
( )
(0)
t
En opposition de phase
¢¡£
¤¦¥¨§©§¨£¨¥¢©
{ d k }
G(f)
Filtre
de forme
A B C H r (f) D
Porteuse émission
A·cos(ω 0 t) BABG
centré de
DSP N 0 /2
Filtre de
réception
Questions :
D’après le schéma ci-dessus, calculer l’énergie moyenne émise par symbole et par bit
pour une MIA-M où { d } est une suite i.i.d. équiprobable et d ∈ { ±1 , ± 3 ,…, ± ( M −1)}
k
Quel est le rapport signal à bruit Eb
/ N 0 pour une MDP-2 avec un formant g( t)
rectangulaire et normé
Quelle est la puissance de la porteuse seule en sortie du filtre H r
Quelle est la puissance du bruit seul en sortie du filtre H r
Pour la MDP-2 avec un formant g( t ) rectangulaire, exprimer le rapport signal à bruit
E / N 0 en fonction de la bande équivalente de bruit du filtre passe-bande :
b
k
B
éq
∆
=
⌠ +∞ 2
⎮ ( )
⌡−∞
2
2 H ( f0
)
H f df
.
29

¥§¦©¨ ¨ §¨
¢¡¤£
!"$#%&%#'%&(
C
Pour une suite numérique, l’estimateur ergodique de la probabilité d’erreur est le taux
d’erreur défini par :
Questions :
nombre d' erreurs observées
nombre de symboles reçus
Déterminer avec quel degré de confiance on peut obtenir une précision de 5% sur l’écart
relatif du taux d’erreur en observant environ 1000 erreurs.
Déterminer le nombre d’erreurs à observer pour une précision de 20% sur l’écart relatif
du taux d’erreur avec une probabilité de ne pas se tromper de 95%.
)¢*+
012§345607 ,86$9:9;-56=¢33=
Soit le schéma synoptique suivant (en équivalent Bande de Base) :
,.-/
d k = b k ⊕ d k−1
{ b k }
Binaire
à
Binaire par
transition
Suite binaire
Suite binaire
par transition
Codage
Binaire
à M-aire
{ d k }
d k ∈ {0,1}
x(t)
Formant
Filtre
passebas
y(t)
Réponse impulsionnelle = r(t)
A B B BB B B B B @
T
z(t)
×(−1)
z 1 (t)
+∞
( ) ∑ k
avec la règle de codage
Le signal x t = a ⋅δ
( t − kT )
k=−∞
+∞
∑
Le signal y t = x t ∗ r t = a ⋅ r ( t − kT )
( ) ( ) ( ) k
k=−∞
Le signal z( t) = y( t) ⋅ y( t − T)
et z1 ( t) = − z( t)
.
⎧ak
= −1 si dk
= " 0"
⎨
⎩ak
= +1 si dk
= " 1"
30

Question : Construire y(t), z(t) et z 1 (t) correspondant à la séquence ci-dessous :
Suite
Binaire {b k }
T
Suite
Binaire {d k }
+1
x(t) 0 T
6T
7T
9T
−1
2T 3T 4T 5T
8T
10T 11T 12T 13T
NB : Pour la construction de y(t), z 1 (t) et z(t), on reprendra les conditions posées à la
remarque (1) de la 1 ère partie.
31