非线性光学讲稿（8）

第八章 光折变非线性光学
国家自然科学基金委员会
数理学部实验物理讲习班
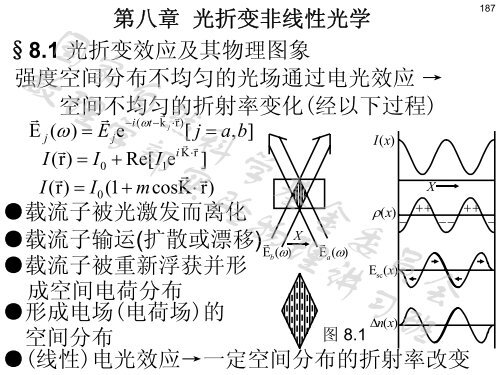
§8.1 光折变效应及其物理图象
强度空间分布不均匀的光场通过电光效应 →
空间不均匀的折射率变化(经以下过程)
−i(
ωt−k
j ⋅r)
E j ( ω)
= E je
[ j =
i K⋅r
I(
r)
= I0
+ Re[ I1e
]
I r)
= I ( 1+
mcosK⋅
r)
( 0
a,
b]
I(x)
●载流子被光激发而离化
ρ(x)
−
X
●载流子输运(扩散或漂移)
Eb( ω)
Ea( ω)
●载流子被重新浮获并形
Esc( x)
成空间电荷分布
●形成电场(电荷场)的
Δn(x)
空间分布
图 8.1
●(线性)电光效应→一定空间分布的折射率改变
X
187
+ + + +
−− −

2 2 ∗
188
I0
= | Ea
| + | Eb
| I1
= 2Eb
⋅ Ea
b a k k K
= − m = (| I1
| / I0)
令 m = 1 K//x →
I ( x)
= I0(
1+
cos Kx)
ρ ( x) = ρ0
cos Kx
∵∇ ⋅ε
⋅ Esc = ρ(
r)
= ρ(
x)
∴E sc(
x) = ρ0(
K/
K⋅ε
⋅ K)
sin Kx
线性电光效应→ Δn(
x)
∝ Esc(
x)
-折射率栅
( x), Δn(
x)
I(x)
国家自然科学基金委员会
数理学部实验物理讲习班
★注意: Esc 与 有一定的相位差
m = 1时相位差为90º,光的干涉条纹(实线)和光折变
形成的折射率栅(虚线)之间有1/4间隔的移位
★不同于此前讨论的光感生折射率变化,例如:
三阶极化产生的光感生折射率栅,没有这种相移
●能产生光折变效应的介质必须具有线性电光效应
因此它们都是非中心对称介质,例如:
各种电光晶体 BaTiO3、LiNbO3、SBN、
KNSBN、GaAs、InP,等等

§8.2 光折变的能带输运模型
单中心能带输运模型
ω
(Kukhtarev模型 )
−
e
图 8.2
189
C
•
V-价带 C-导带 D-施主
A-受主,图中载流子是电子
•
• •
•
•
•
•
•
• •
D
A
施主参与光折变过程,受主
V
出现只为在无光照时介质保持电中性 + ′ A − D = 0 N N N
N′
D = sI ( N
N
D − N′
D)
−γ
RNN
′ D
∂t
∂N ∂N′
D 1
− = ∇ ⋅ j
∂t
∂t
q
j = qNμ
⋅ E+
kBTμ
⋅∇N
( E)
( r)
( A D)
N N N q − + − = = ⋅ ⋅
-导带中电子数密度
N A,
ND
(8.1) -受主,施主数密度
N′ D -离化施主数密度
(8.2)
I -光强
s-光激发截面 j-电流密度
γ
(8.3) R-电子与空施主的复合率
ε ρ
μ − q-电子电荷
(8.4)
-迁移率
k -波尔兹曼常数 T-温度
∂
∇
国家自然科学基金委员会
数理学部实验物理讲习班
B

sI( N − ′ ) − ′
D ND
γ RNN
D = 0 ∇ ⋅ j = 0
j = qNμ
⋅ E + kBTμ
⋅∇N
E)
(
) N N N q
∇ ⋅ ε ⋅ = − + − ′
稳态情形→
190
(8.5) (8.6)
国家自然科学基金委员会
数理学部实验物理讲习班
(8.7) (8.8)
( A D
●均匀光照 因所有物理量的空间变化均为零,故:
+ ′ A − D = 0 N N N
若 N 〈〈 N A (导带电子很少), R A (光较弱),由
(8.5)和(8.9) →
N sI γ 〈〈
(8.9)
N − N
N − N
N
D A = sI N′
D A
D = N A + sI
γ RN
A
γ RN
A
I r)
= I ( 1+
mcosK⋅
r
●光强为周期性空间分布 ( 0
)
若 m 〈〈 1 且忽略高次空间谐波项,近似有:
⋅
⋅
i K r
i K r
N ( r)
= N0
+ Re{
N1e
} N′
( r)
= ′ 0 + Re{
′
D ND
ND1e
}
i K⋅r
i K⋅r
j ( r)
= j0
+ Re{
j1e
} E(
r)
= E0
+ Re{
E1e
}
i K⋅r
I(
r)
= I + Re{
I e }
脚标带‘0’的量为该物
0 1
理量的空间均匀部份;周期变化部份为其一级小量

191
稳态有: →
=
×
∇
=
×
∇
⋅
0
)
e
(
E
r
K
1
i
E →
=
× 0
K 1
E
K
//
1
E
利用(8.5)- (8.8)解得:
0
0
sI
N
N
N
N
A
R
A
D
γ
−
= 0
0
sI
N
N
N
N
N
A
R
A
D
A
D
γ
−
+
=
′
0
1
2
0
2
2
0
1
)
/(
E
K
/
1
)
/(
E
K
)
/
(
I
I
Tk
k
iq
k
K
K
q
T
k
iK
E
D
B
D
B ×
〉
〈
⋅
⋅
−
+
〉
〈
⋅
⋅
−
−
=
μ
μ
μ
μ
(在光强较弱以至 的情况下)
A
R N
sI γ
〈〈
0
2
0 A
R
D
N
sI
N γ
〈〈
)
(
2
2
A
D
D
A
B
D
N
N
N
N
T
k
q
k −
〉
〈
= ε
2
K
K
K
⋅
⋅
=
〉
〈
ε
ε 2
K
K
K
⋅
⋅
=
〉
〈
μ
μ
(8.10)
当 时,
A
D
N
N 〉〉
T
k
N
q
T
k
N
q
k
B
D
B
A
D
〉
〈
′
≅
〉
〈
=
ε
ε
0
2
2
2
0
E
恒场 一般是外加的,且令 ,此时(8.10)→
K
//
E 0
0
1
2
0
2
2
0
1
)
/(
E
/
1
E
)
/
(
I
I
Tk
k
iqK
k
K
q
T
k
iK
E
D
B
D
B ×
−
+
−
−
= (8.11)
国家自然科学基金委员会
数理学部实验物理讲习班

当 E0 = 0(空间电荷场的形成,全来自载流子扩散)→
国家自然科学基金委员会
数理学部实验物理讲习班
E
§8.3 空间电荷场
引入参量: d
1
− iK(
k
T
/ q)
B 1
= × (8.12)
2 2
1+
K / kD
I0
E = K(
kBT
/ q)
/( K)
qN E (8.12)→
q = A 〈 ε〉
− iEd
I1
E1
=
× (8.13)
1+ ( Ed
/ Eq)
I0
− iEd
1−
i[E0/
Ed
] I1
(8.11)→ E1
= {
} ×
1+ ( Ed
/ Eq)
1−
i[E0/(
Ed
+ Eq)]
I0
E0 = 0 : i K⋅r
i K⋅r
E 1e
∝ −iI1e
[ K r ( / 2)]
1e
i ⋅ − π
= I
( π / 2 相位差) d q E E E 1 , 〈
E
图 8.3
1
Λ = 2π / K
Eq ~ Λ
Ed
-直线 Ed ~ Λ-固定的双曲线
Ed
2 1/
2
= Eq
→ Λ D = 2π [ k BT
〈 ε〉
/( q N A)]
1
1/
2
| | = ( N k T / 〈 ε〉
) m
E1 max A B
I
ΛD
192
(8.14)
E
q
Λ

Λ | ≈ E m ∝ Λ
| E1 q
−193
1
▲ 很小时, ; Λ 很大时, | E1 | ≈ Edm
∝ Λ
1 max | ▲ | E 随 N A 增大而增大,随 〈ε 〉 增大而减小
因无光照时 + ′ A − D = 0 → N N N A D N N ≅ ′ ( 因 N很小)
→ 1 max随无光照时的离化施主浓度
增大而增大
| | E D N′
▲直线 Eq ~ Λ 的斜率正比于 A,反比于
;曲线
与材料参数无关
N 〈ε 〉
Ed
~ Λ
(亦称作有效载流子浓度)
§8.4 线性电光效应与三维光折变光栅
线性电光效应又称Pockels效应(折射率变化与作用
电场的一次方成正比),实质上也是一种二阶非线性
光学效应,故亦只可能在非中心对称介质中产生
光波 ) 与直流电场 混频→频率为 的极化:
E
ω
国家自然科学基金委员会
数理学部实验物理讲习班
E(ω 1
( 2)
( 2)
P ( ω) = χ ( −ω,
0,
ω)
E1E(
ω)
→ Δn(
ω)
∝
E
1

各向异性介质中折射率是用折射率椭球表征,在任
意直角座标系 中该椭球表为如下方程:
1 3
∑ = 1
−
O -ξ1 , ξ2,
ξ3
η ξ (8.15) ηij(
i,
j = 1,
2,
3)
→η
= ∑ ηij
ai
国家自然科学基金委员会
数理学部实验物理讲习班
i,
j
ij iξ
j
η ⋅ε = ε
0 (8.16)
在主轴座标系 ηij
i
η
ii
( ≠ j)
= 0
ε ε = n
−2
= 0 / ii i
ε -介质的介电张量
n i
( i = 1,
2,
3)
i,
j=
1,
2,
3
194
a
-主折射率
●线性电光效应表述为: Δη
ij = ∑rijk
Ek
(8.17)
k
rijk -电光系数, 与之相应有 ε
ij 且 + Δη)
⋅(
ε + Δε
)
忽略
Δη ⋅ Δε
→
Δ ( η = ε0
− ε ⋅ Δη
⋅ε
Δε
=
ε
2
Δε
= −ε
n n Δη
在主轴座标系 ij 0 j ij
{ }[ i,
j,
k =
r ijk
1,
2,
3]
0
2
i
(8.18)
(8.19)
-构成(线性)电光张量
j

195
→
= ji
ij
η
η
∵ →
= jik
ijk
r
r lk
ijk
r
r =
可令
)
21
(
)
12
(
),
13
(
)
31
(
),
32
(
)
23
(
),
33
(
),
22
(
),
11
(
)
( 和
和
和
ij =
6
,
5
,
4
,
3
,
2
,
1
=
l
3
,
2
,
1
6
,
5
,
4
,
3
,
2
,
1
}
{
=
=
k
l
lk
r
→
= ]
3
,
2
,
1
,
,
}[
{ k
j
i
r ijk
∑
=
Δ
k
k
lk
l
r E
η
→
∑
=
Δ
k
k
ijk
ij
r E
η (8.20)
▲电光张量亦要
反映该介质的结
构对称性,具有相
同结构对称性的
不同介质,其电光
张量对称性相同
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
0
0
0
0
0
0
0
0
0
0
0
0
0
42
42
33
13
13
r
r
r
r
r
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
−
−
0
0
0
0
0
0
0
0
0
0
22
51
51
33
13
22
13
22
r
r
r
r
r
r
r
r
4mm(如BaTiO3 ) 3m(如LiNbO3)
国家自然科学基金委员会
数理学部实验物理讲习班

BaTiO3:
LiNbO3:
r 42
−2
= 820×
10 m / V r13
= 8×
10
r
−12
= 8.
6×
10 r
−12
= 3.
4×
10
13
三维光折变光栅
i K⋅
r
己知: ( r)
= I0
+ Re{
I1e
} →空间电荷场
22
−12
r33
= 2.
8×
10
−12
r51
= 28×
10
r = 30.
8×
10
国家自然科学基金委员会
数理学部实验物理讲习班
I sc
i K⋅r
E = Re{ E1e
}
r
sc
Δηij
( r)
= ∑r
ijk Ek
( r)
k
E = cos( K⋅
r)
sc sc sc
E E
sc
Δηij
( r)
= ( ∑rijk
Ek
) cos( K⋅
r
k
K ⋅ r = C
(8.22)
Δηij r
C
2π C K
K ⋅ r = C
K
K
(8.21)
Λ = 2π / K
→介质在任一位置 处的折射率椭球将发生变化:
将 写为 ,则 )
▲ 时 不随 改变,常数 改变时,将
以 为周期随 改变; 是一个与矢量 正
交的平面→在垂直于的 任一平面内,都有相同的
折射率椭球;沿着 的方向,该椭球的大小形状周期
性改变,周期为 (三维光折变光栅)
33
−12
196
−12

▲光折变光栅相对光强空间周期分布有一定相移
●如何得到该光栅对任意传播方向两个本征偏振态
(o-光和e-光)的折射率空间周期性分布(折射率栅)?
设: d -本征偏振方向的单位矢量; nd
-相应的折射率
1
= d ⋅η
⋅ d
(8.23)
国家自然科学基金委员会
数理学部实验物理讲习班
2
nd 以4mm对称的BaTiO3为例:(图10.4)
−i(
ωt−k
a ⋅r)
−i(
ωt−k
b ⋅r)
Ea
( ω)
= Eae
Eb
( ω)
= Ebe
sc sc
E = E cos( K⋅
r)
[ K kb
− ka
// K
∵ sc sc sc sc
∴ E = a x E sinθ
+ a z E cos
= 在ac面]
→
E θ
由(8.21)→
⎛r
⎜
Δη
= ⎜
⎜
⎝ r
13
42
cosθ
0
sinθ
r
13
0
cosθ
0
r
r
42
33
sinθ
⎞
⎟
0 ⎟E
cosθ
⎟
⎠
sc
k
k
cos( K⋅
r)
(8.24)
a
b
z//c
x//a
c
(a)
θ
a
图 8.4
197
K

z//c
α K
找出沿 (在xz平面内)传播的o-光和e-光的折射率栅
o-光:垂直于xz平面偏振
k
国家自然科学基金委员会
数理学部实验物理讲习班
θ
a 2
e-光:平行于xz平面偏振并垂直
k
do
=
de(
α ) = −cosα
a1+
sinα
a3
1
由(8.23)→ Δ( ) = d ⋅ Δη
⋅ d
2
nd 1 3 1−3
Δnd = − nd
( d ⋅ Δη
⋅ d ) Δη
= ∑Δηij
aia
j
2
i,
j
3
sc
d = do
→ Δno
= −(
1/
2)
nor13(cosθ
) E cos( K⋅
r)
d = de(α
) →
3
2
Δne(
α ) = −(
1/
2)
ne
( α )( r13
cosθ
cos α − r42
sinθ
sin 2α
2 sc
+ r cosθ
sin α)
E cos( K⋅
r)
33
BaTiO3晶体 42 r33,r
13
r 〉〉
= 45
•
图 8.4 (b)
(8.25)
k
198
x//a
(8.26)
→ α 有最大的 ne(α
)
能形成最大的折射率栅
Δ

§8.5 光伏效应及其对光折变的影响
国家自然科学基金委员会
数理学部实验物理讲习班
I
199
图 8.5
光均匀照射非中心对称的铁电晶体
−
+
→自发极化方向(c轴)两端面间有 − j +
−
+
−
+
光感生电压
−
+
−
Ephv
I-光强 +
光伏电流密度 j = GαI
α-吸收系数
G -Glass系数
向晶体两端充电,形成恒定电场 E phv
j −σ E phv = GαI
−σ
E phv = 0 σ -电导率
σ ≅ KI (忽略暗电导) E ≅ Gα
/ K -光伏电场
▲光伏效应为载流子输运提供新途径并影响光折变
4 5
E phv = 10 ~ 10 V / cm
3
通过电光效应→ 10 −
Δn ≈
光伏效应的描述
光场复振幅 E = E1
a x + E2
a y + E3
a z
→
phv
j = j
a
1 a x + j2
a y + j3
z

j
= β : EE
∗
∗
200
ji
= ∑ βijkE jEk
β
j,
k
→ −E,
j → − j 后,(8.27)仍成立→ β = 0
∗
j
β = β
(8.27) (8.28) -光伏张量
国家自然科学基金委员会
数理学部实验物理讲习班
E
中心对称介质:
β ijk ( i,
j,
k = 1,
2,
3)
一般是复数, i是实数
s a
β = β + iβ [ β = β + iβ ]
ijk
s
ijk
a
ijk
s s
β ijk = βikj
称为对称部份
ikj
ikj
ikj
a a
βijk −β
ikj
E
E = + a
●设光波沿x方向传播: y z E a 2 3
A E = E
−iδ
= A e A , , δ − 实数]
2
2
3
3
[ 2 3 A
→ ijk ikj
= 称为反对称部份
δ = 0,
π -线偏振 δ = ± π / 2-圆偏振
其它-椭圆偏振
由(8.28)→ ji ∗
∗
= βi
23 E2E3
+ βi32E3E2
( i = 1,
2,
3)
iδ
−iδ
ji
= βi
23 A2
A3e
+ βi32A3
A2e
( i = 1,
2,
3)
线偏振: = = →
− iδ
iδ
e e 1
只来自对称部份
s
ji
= ( βi
23 + βi32)
A2
A3
= 2βi
23A2
A3
( i = 123)
-线光伏电流

201
圆偏振:
→
±
=
±
i
i 2
/
e π
∵
)
123
(
2
)
( 3
2
23
3
2
32
23
=
=
−
±
= i
A
A
A
A
i
j
a
i
i
i
i
β
β
β ∓
只来自反对称部份-圆光伏电流
★光伏张量的对称性亦应反映介质的结构对称性
→
= )}
3
,
2
,
1
,
,
(
{ k
j
i
ijk
β )}
6
,
5
,
4
,
3
,
2
,
1
3
,
2
,
1
(
{ =
= l
i
il
β
→
= 12
,
23
,
31
,
33
,
22
,
11
jk 6
,
5
,
4
,
3
,
2
,
1
=
l
∗
= ijk
ikj
β
β
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
0
0
0
0
0
0
0
0
0
0
33
31
31
14
22
22
22
14
β
β
β
β
β
β
β
β
LiNbO3
3m:
4mm:
BaTiO3
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
0
0
0
0
0
0
0
0
0
0
0
0
0
33
31
31
14
14
β
β
β
β
β
)
//
( C
Z
31
33
22
14
,
, β
β
β
β 〈〈
沿z轴(即c轴)
光伏电流最大
国家自然科学基金委员会
数理学部实验物理讲习班

光伏效应对空间电荷场的影响
●光场为线偏振:
设干涉场的光强分布为 I( z)
I0
I1
cos Kz + =
光伏电流为 jphv jphv
a z
= pI p
国家自然科学基金委员会
数理学部实验物理讲习班
(8.1)-(8.4)应修正为:
∂N ∂N′
D 1 ∂j
= +
∂t
∂t
q ∂z
E
( A
z
N N N q ∂
ε = − + − ′
∂
D
202
,沿z方向
jphv = ( 与光伏系数有关)
∂N′
D = sI ( N D − N′
D)
−γ
RNN
′ D (8.29)
∂t
∂N
j = qNμ
E+
kB
Tμ
+ pI
∂z
)
(8.30) (8.31)
(8.32)
解之得稳态空间电荷场为:
(E0
− E
E1
= −E
q [ 2
E0
+ ( Ed
(Ed
+ Eq
) E
tanφ
=
(E − E
0
phv
d
phv
2 2 1
) + Ed
I 2 ] × 2
+ Eq)
I
+ E0(E0
− E
) E − E E
q
phv
d
1
0
phv
)
Esc 1 φ
= E cos( Kz + )
pγ
RN
A
E phv =
qsμ(
N − N
D
是均匀光照形成
的稳态光伏电场
A
)

●两束入射光是正交(线)偏振
不能产生干涉→不形成光强空间周期分布→
若不考虑光伏效应,就不能产生光折变光栅
−i(
ω t−k1
z)
i t
沿同一方向传播情形: E x = Ae
E y e A
−
=
(o-光和e-光) k 1 = n1ω
/ c,
k2
= n2ω
/ c
−iδ
( z)
−i(
ωt−k1
z)
叠加后→ E = E a + E a = A[
a + a e ] e
国家自然科学基金委员会
数理学部实验物理讲习班
x
x
y
y x y
( ) = ( k2
− k1)
z = [( n2
n1
−
( ω k2
δ z − ) ω / c]
z
δ ( z) = 0和
π
2
δ ( z ) = π / 2和
3π
/ 2 -(圆)
▲故光波的偏振态亦
将随z改变: -(线)
δ (z)
= 其它 -(椭圆) [ π为周期]
Λ = 2π /( k2 − k1)
) n = λ n −
/( 2 1
→来自光伏效应
的光折变光栅
P :
图 8.6
Z = 0
随z变化周期为:
Λ
4
Λ
2
3Λ
4
203
z)
Λ

204
交义传播情形:
)
r
k
(
2
2
)
r
k
(
1
1
2
1 e
a
e
a
E
⋅
−
−
⋅
−
−
+
=
t
i
t
i
A
A
ω
ω
叠加后→
2
1
a
a
⊥
1
e
|
| 1
1
φ
i
A
A
−
=
2
e
|
| 2
2
φ
i
A
A
−
=
例:LiNbO3晶体
e
o
e
o
a
a
,
a
a
,
k
k
,
k
k
2
1
2
1
=
=
=
=
两光束在x-y平
面内(z为光轴)
偏振态也将空间周期性变化
→ 感生另类光折变光栅
z
y
x
j
j
j
j a
a
a 3
2
1
+
+
=
LiNbO3:计算得到
)]
E
E
E
(E
[
)
E
E
E
(E
)
E
E
E
(E 1
3
3
1
14
1
2
2
1
22
1
3
3
1
14
1
∗
∗
∗
∗
∗
∗
−
+
+
−
+
=
a
s
s
i
j β
β
β
)
E
E
E
(E
E
E
E
E 1
3
3
1
14
2
2
22
1
1
22
2
∗
∗
∗
∗
+
+
+
−
=
s
s
s
j β
β
β
)]
E
E
E
(E
[ 2
3
3
2
14
∗
∗ −
+
a
i β
∗
∗
∗
+
+
= 3
3
33
2
2
13
1
1
13
3
E
E
E
E
E
E
s
s
s
j β
β
β
)
E
,
E
,
(E
E 3
2
1
o
a
s
e
A
A
j a
)]
r
K
sin(
)
r
K
cos(
[
|
|
2 14
14
0
φ
β
φ
β +
⋅
+
+
⋅
=
o
e k
k
K
−
= o
e
φ
φ
φ −
=
(8.33)
o
j a
//
故垂直于z并落在xy平面,
其大小沿 方向作空间周期性变化 ( )
K
|
K
|
/
2
π
=
Λ
国家自然科学基金委员会
数理学部实验物理讲习班

形成的光折变光栅是两个光栅的叠加,分别来自该
右边的第一项(对称部份)和第二项(反对称部份),
互有 π / 2相移
国家自然科学基金委员会
数理学部实验物理讲习班
(a)
(b)
(c)
(d)
图 8.7
n
o
ne
k
o
• e
K
k
Λ
e
o
205

§8.6 光折变两波耦合
局域响应:任一点的响应
只与该点的光场有关
非局域响应:还与邻近其
它点的光强有关
▲两束同频率的光在局域
介质中不存在稳态能量交换
光强 响应
▲光折变介质是非局域响应介质,两束同频率的光存
在稳态定向能量交换-两波耦合 x
国家自然科学基金委员会
数理学部实验物理讲习班
同向两波耦合(左)
反向两波耦合(右) a
图 8.8
z = 0 L z = 0 L
206
a
b b
θ θ
z

−i(
ωt−k
a ⋅r)
a(
ω)
= Eae
2 2
I 0 = | Ea
| + | Eb
|
I
⋅
⋅
b(
= b
= 0 + 1
∗
1 = 2Eb
⋅ Ea
b a k k K
= −
sc
E
−i(
ωt−k
r)
207
b
i K r
ω ) E e I(
r)
I Re[ I e ]
国家自然科学基金委员会
数理学部实验物理讲习班
sc
→光折变光栅: Δηij = ∑r
E k ( i,
j = 1,
2,
3)
(8.34)
k
2 2
2 sc
或 Δε = −ε
n n Δη
= −ε
n n ∑ r E ( i,
j = 1,
2,
3)
(8.35)
ij
0
i
j
ij
0
ijk
2
i
[在主轴座标系, i j 为主折射率,见式(8.19)]
n n ,
sc
i K⋅r
−iφ
∗ −iφ
∵E
= Re{
E1e
} E1
∝ ( I1
/ I0
) e ∝ ( Eb
⋅ Ea
/ I0
) e
[ φ -空间电荷场相对干涉条纹的相移]
∗
1 ( 1)
i Ea ⋅ E
− φ b i K⋅r
( 1)
Δε
ij = εij
e e + c.
c.
(8.36) [ εij
是比例系数(实)]
2 I0
( 1)
(
1)
{ εij
} = ε
∗
1 (
1)
i Ea ⋅ E
− φ b i K⋅r
Δε
= ε e e + c.
c.
2 I
(8.37)
0
Δε
→ Δ P = ( Δε
) ⋅ E = ( Δε
) ⋅[
Ea
( ω)
+ Eb
( ω)]
P P
) 3 (
= Δ
j
k
ijk
k
E

208
由(8.37)知:
+
+
= )
k
,
(
P
)
k
,
(
P
P
)
3
(
)
3
(
)
3
(
b
a
ω
ω
)
r
k
(
)
1
(
0
)
3
(
e
e
)
a
a
)(
a
(
2
1
)
k
,
(
P
⋅
−
−
∗
⋅
⋅
=
a
t
i
b
a
b
i
b
a
b
a
E
E
E
I
ω
φ
ε
ω
)
r
k
(
)
1
(
0
)
3
(
e
e
)
a
a
)(
a
(
2
1
)
k
,
(
P
⋅
−
−
∗
−
⋅
⋅
=
b
t
i
a
b
a
i
b
a
a
b
E
E
E
I
ω
φ
ε
ω
(8.38)
(8.39)
(8.40)
b
a a
,
a
[ 光波 偏振的单位矢量]
b
a,
)
k
(
P
)
(
E
)
(
E
)
3
(
2
0
2
2
a
a
a
k
,
ω
ω
μ
ω
ω −
=
+
∇
)
k
(
P
)
(
E
)
(
E
)
3
(
2
0
2
2
b
b
b
k
,
ω
ω
μ
ω
ω −
=
+
∇
2
2
2
0
2
2
2
/
|
k
|
|
k
| c
n
k b
a
ω
=
≅
=
)
k
(
P
a
)
(
E
)
(
E
)
3
(
2
0
2
2
a
a
a
a
k
,
ω
ω
μ
ω
ω ⋅
−
=
+
∇
)
k
(
P
a
)
(
E
)
(
E
)
3
(
2
0
2
2
b
b
b
b
k
,
ω
ω
μ
ω
ω ⋅
−
=
+
∇
因振幅都只是z的函数,用z方向的缓变振幅近似:
)
,
(
|
/
a
k
|
|
/
|
2
2
b
a
j
dz
dE
dz
E
d j
z
j
j
=
⋅
〈〈
(8.41)
(8.42)
国家自然科学基金委员会
数理学部实验物理讲习班

209
a
b
b
i
b
a
b
a
a
az
E
E
E
I
i
dz
dE
k
∗
⋅
⋅
⋅
=
φ
ε
μ
ω
e
)
a
a
)(
a
a
(
2
2
)
1
(
0
0
2
b
a
a
i
b
a
b
a
b
bz
E
E
E
I
i
dz
dE
k
∗
−
⋅
⋅
⋅
=
φ
ε
μ
ω
e
)
a
a
)(
a
a
(
2
2
)
1
(
0
0
2
)
,
(
a
k b
a
j
k z
j
jz
=
⋅
=
(8.43)
(8.44)
同向两波耦合情形 0
, 〉
bz
az k
k
θ
λ
π
θ cos
)
/
2
(
cos 0
n
k
k
k bz
az
=
=
=
a
a
b
a E
E
E
I
dz
dE
2
|
|
2
1 2
0
α
−
Γ
−
=
b
b
a
b E
E
E
I
dz
dE
2
|
|
2
1 2
0
α
−
Γ
=
∗
加进吸收系数 后:
α
φ
ε
θ
λ
ε
π i
b
a
b
a
n
i e
)
a
a
)(
a
a
(
cos
)
1
(
0
0
⋅
⋅
⋅
−
=
Γ
(8.45)
(8.46)
(8.47)
令
a
i
a
a
I
E
ψ
e
= →
=
b
i
b
b
I
E
ψ
e 光强和相位的
耦合波方程:
国家自然科学基金委员会
数理学部实验物理讲习班

dI
dz
dI
dz
γ
I I
−α
(8.48)
dψ
a = β
dz I
γ
I I
−α
(8.49)
dψ
b = β
dz I
π (
1)
γ = ( a a⋅
ε ⋅a
b)(
a a⋅
ab
) sinφ
ε0n0λ
cosθ
π (
1)
β =
( a a⋅
ε ⋅a
b)(
a a⋅
ab
) cosφ
2ε
0n0λ
cosθ
Γ = γ − 2iβ
d
( Ia
+ Ib
) = 0
dz
γ 称为耦合常数
α = 0
〉 0 :
I → I
a a b = − Ia
Ia
+ Ib
b a b = Ib
Ia
+ Ib
a
a
Ib
+ I
Ia
+ I
国家自然科学基金委员会
数理学部实验物理讲习班
b
b
(8.52)
(8.53)
▲忽略吸收(即令 ),由 (8.48)、 (8.49)→
γ Ia Ib a b
γ 〈 0 : Ia Ib Ib → Ia
两光波光强之和不随z变
(8.50)
210
(8.51)
两波耦合(定向,
与谁大谁小无关)

φ = / 2 γ
▲由(8.52)知, π 时, 最大,两波耦合最强;
φ = 0时
γ = 0,两光波不会交换能量→
局域响应介质不存在两波耦合
▲耦合常数的正负,由许多因素决定,例如两入射光
相对晶体晶轴的方向,晶体中载流子的类型,等等
如图8.9的配置,空穴型 γ 〉 0,
Ia → Ib
α1 α2
电子型 γ 〈 0,
I c
b → Ia
▲一般说来,相位 ψ a, ψ b 要随z改变,但
从(8.53)知, φ = π / 2时例外因此时
β = 0 b a 图 8.9
反向两波耦合情形 cosθ ( 2π
0 / λ)
cosθ
n
k k kaz = − bz = =
dIa
IaI
b
dψ
a Ib
= −γ
−αI
a (8.54) = β (8.56)
国家自然科学基金委员会
数理学部实验物理讲习班
dz
dI
dz
Ia
+ Ib
IaI
b −γ
+ α
I + I
b =
Ib
a b
(8.55)
dz
dψ
b
dz
I
a
= −β
I
+ Ib
Ia
+ I
a
b
211
(8.57)

d
dz
忽略吸收→ ( I I ) = 0
a
− b
国家自然科学基金委员会
数理学部实验物理讲习班
▲在光波相互作用中,总光强仍是不变的,因光波
和光波 a 的传播方向
γ 〉 0 : (z)
I a
γ 〈 0 : (z)
I a
Ib (z)
Ia → Ib
(z)
I → I
Ib b a
▲相位一般也要随z改变,除非 φ = π / 2
d
∵ ( ψ b − ψ a)
= −β
ψ b −ψ a = −βz
+ const.
dz
= b − a
2k
k k K
K′
= ( k
b−
ka
) − β a z
= K−
β a z
▲ -栅: θ = 0时,两光波相向传播
K′
= K − β
K = kb
− ka
= 2k
b(
K = 2k)
a b
光折变光栅的波矢由 →
→受激光折变背向散射(SPB)
212
b

213
耦合常数的计算 φ
ε
θ
λ
ε
π
γ sin
)
a
a
)(
a
a
(
cos
)
1
(
0
0
b
a
b
a
n
⋅
⋅
⋅
=
光波 和光波 →空间电荷场:
a b
r
K
1 e
E
⋅
−
=
i
sc E )
K
//
( 1
E
0
1
2
0
2
2
0
1
)
/(
E
/
1
E
)
/
(
I
I
Tk
k
iqK
k
K
q
T
k
iK
E
D
B
D
B ×
−
+
−
−
=
也可表示为: )
/
(
e 0
1
1
I
I
E
E
i
s φ
−
=
)
/(
E
K
/
1
)
/(
E
K
)
/
(
e 2
0
2
2
0
〉
〈
⋅
⋅
−
+
〉
〈
⋅
⋅
−
−
=
−
μ
μ
μ
μ
φ
D
B
D
B
i
s
Tk
k
iq
k
K
K
q
T
k
iK
E
)
K
//
(
)
(
s
E
s
E 是 的量值,是与光强无关的实数
若 则因
0
E 0 =
→
= 2
/
π
φ
2
2 /
1
)
/
(
D
B
s
k
K
q
T
k
K
E
+
=
其中
)
r
K
(
0
)
r
K
(
0
1 e
e
E
φ
φ +
⋅
−
∗
+
⋅
−
⋅
=
=
i
b
a
s
i
s
sc
I
E
E
E
I
I
E
于是:
)
3
,
2
,
1
(
e
E
)
r
K
(
0
=
⋅
=
+
⋅
−
∗
k
I
E
E
E
i
b
a
s
k
sc
k
φ
或
(8.58)
(8.59)
(8.60)
(8.61)
(8.62)
s
E
[(8.52)]
国家自然科学基金委员会
数理学部实验物理讲习班

将其代入下式:
国家自然科学基金委员会
数理学部实验物理讲习班
2 2
2 2 sc
Δεij = −ε0
ni
n jΔηij
= −ε0ni
n j ∑ rijk
Ek
( i,
j
k
∗
1 ( 1)
i Ea ⋅ E
− φ b i K⋅r
Δεij
= εij
e e + c.
c.
2 I0
s
= − n n ∑r
E
2 2
( 1)
2ε
= 1,
2,
3)
并与式 [(8.36)] 比较→
ε ij
0 i j ijk k (8.63)
k
1 = ∑
i,
j
ε
E0 ≠
ε
214
[(8.35)]
( 1)
ij
a a
▲从此式,若己知电光张量,即可算出
i j
若无外加电场 φ = π / 2 ,若 0 , φ可由(8.59)求出
再用(8.52)便可得到 γ
⎛ 0 0 γ ⎞
x//a
z//c
c
α
K
BaTiO3:
a
a { γ ijk}
= { γ lk}
2θ
b
图 8.10 n 1 = n2
= no,
n3
= ne
⎜
⎜ 0
⎜ 0
= ⎜
⎜ 0
⎜γ
⎜
⎝ 0
42
γ
0
0
42
0
0
γ
γ
13
13
33
0
0
0
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠

K →
s s s
E E = E α a + cosα
a )
计算出不为零张量元:
( 1)
ε = − n cosαE
33
4
2ε0 e r33
(sin x
z
s
( 1)
( 1)
11 = ε22
( 1)
( 1)
13 = ε31
=
国家自然科学基金委员会
数理学部实验物理讲习班
ε = n cosαE
ε − n sinαE
4
−2ε
0 or13
2 2
2ε0 one
r42
因BaTiO3基本上是单轴晶→两光波都是o-或e-光
都是o-光: (这里不考虑光伏效应! )
y a a a
a = b = n 0 = no
2π
3 s
γ o 13 cosα
sinφ
λ cosθ
E r n − =
用(8.52)→
(8.64)
都是e-光: a a = cosθ
1 a x + sinθ1
a z ab = cosθ
2 a x + sinθ
2 a z
π
π n 0 = ne
( α ) a
θ1 = + θ −α
, θ2
= −θ
−α
2
2 假定 θ 很小 2θ
2 2 2 2 −2
ne( α ) = [cos α / ne
+ sin α / no
]
b
2π
4
用(8.52)→ γ = −cos2θ
[cosθ1
cosθ2no
r13
cosα
n ( α)
λ cosθ
e
2 2
4
s
+ n r sinα
sin 2α
+ θ sinθ
n r cosα
] E sinφ
no e
42
sin 1 2 e 33
s
s
215
(8.65)

∵r42
〉〉 r13,r
33 →
2π
2 2 s
γ = −cos2θ
none
r42E
sinα
sin 2α
sinφ
n ( α ) λ cosθ
e
时,亦即入射光束相对光轴以 45角入射时最大
▲α
= 45
▲两束e-光的耦合常数比两束o-光要大得多
§8.7 光折变四波混频与光折变全息术
E
国家自然科学基金委员会
数理学部实验物理讲习班
j
=
物理考虑:二波耦合方程改写为
dE
dz
E
j
e
−i(
ωt−k
⋅r)
1
j
( j = a,
b,
c,
d)
kc
−k
b
a ∗
= − Γ(
EaEb
) Eb
-相当于 b 读
2I
0
∗
光折变栅 ( a b ) 向 a衍射
E E
∗ ∗
四波混频有六个栅 ( EaEb
+ EcEd
)
∗ ∗
∗
( E bEd
+ EaEc
) ( b c ) E E ∗
( a d ) E E 通过
分析‘读’和‘衍射’→耦合方程
= kd
= −k
a
b
a
b
a
z = 0 z = L
z = 0
z =
L
216
(8.66)
图 8.11
d
c
d
c

217
透射栅近似:
b
d
c
b
a
a E
E
E
E
E
I
dz
dE
)
(
2
1
0
∗
∗ +
Γ
−
=
a
d
c
b
a
b E
E
E
E
E
I
dz
dE
)
(
2
1
0
∗
∗
∗
+
Γ
=
d
d
c
b
a
c E
E
E
E
E
I
dz
dE
)
(
2
1
0
∗
∗ +
Γ
=
c
d
c
b
a
d E
E
E
E
E
I
dz
dE
)
(
2
1
0
∗
∗
∗
+
Γ
−
=
d
c
b
a
I
I
I
I
I +
+
+
=
0
φ
ε
θ
λ
ε
π
β
γ
i
n
i
i
e
cos
2
)
1
(
0
0
−
=
−
=
Γ
a
a
)
1
(
)
1
(
⋅
⋅
= ε
ε
a
假定四束光具相
同偏振方向
(8.67)
(8.68)
(8.69)
(8.70)
c
b,
设 强(泵光), 弱,可用泵光无消耗近似:
d
a,
0
/
/ =
= dz
dE
dz
dE c
b
]
)
(
|
[|
2
1 2
0
∗
+
Γ
−
= d
c
b
a
b
a E
E
E
E
E
I
dz
dE
]
|
|
)
[(
2
1 2
0
∗
∗
∗
∗
+
Γ
−
= d
c
a
c
b
d E
E
E
E
E
I
dz
dE
(8.71)
(8.72)
2
|
| b
E
2
|
| c
E
c
b E
E
∗
∗
c
b E
E
不变常数
国家自然科学基金委员会
数理学部实验物理讲习班

起始条件为: ( 0)
≠ 0,
E ( L)
= 0
E
a
( z)
= [( e
Ea d
−Γz
/ 2 −ΓL
/ 2
+ qe
)( 1+
qe
−ΓL
/ 2
)] E
∗
∗ −Γz
/ 2 −ΓL
/ 2 −Γ
Ed
( z)
= [( Ec
/ Eb)(
e − e )( 1+
qe
2
q = | Ec
|
2
/ | Eb
| -两泵光的强度比
E ( 0)
∗
E ( 0)
d a
d
∝ a
a
解得:
国家自然科学基金委员会
数理学部实验物理讲习班
( 0)
L / 2
)] E
a
( 0)
218
(8.73)
(8.74)
▲ -光束 是光束 的相位共轭反射光
共轭反射系数
Ed
( 0)
E
∗
∗
c −Γ
L / 2
−Γ
L / 2
ρ = = ( )[( 1−
e ) /( 1+
qe
)]
∗
∗
Ea
( 0)
Eb
2
共轭反射率:
2 sinh( ΓL
/ 4)
R = | ρ | =
cosh[( ΓL
/ 4)
− ln q]
2
sinh ( γL / 4)
φ = π / 2时
R =
q = 1 →
2
cosh [( γL
/ 4)
− ln q]
tanh ( / 4)
1
2
(8.75)
(8.76)
R = γL
≤
/ 2
当 φ ≠ π / 2 e L
2
γ
q =
sinh( ΓL
/ 4)
Rmax
= 可远大于1
cosh( βL
/ 2)
cosh( βL / 2)
= 0 → R = ∞
max

光折变全息术
I
般光学全息术写-读过程:
= | E
Δ
2 2
∗ i K⋅r
| + | | + Re[ 2 e ] a
a Eb
EbEa
K r
Re[ 2 e ]
∗ i ⋅
∝ b a E E n b a k k K
= −
b
P P
国家自然科学基金委员会
数理学部实验物理讲习班
d
图 8.12
该折射率光栅(全息图)包含了物光携带的全部讯息
读光束 c因满足布拉格条件 k 将在光束 d
d = K+
kc
方
∗
∗
向衍射 E d ∝ ( EbEa
) Ec
= ( EbEc
) Ea
携带着物光携带的
全部讯息,并复现被照物体的像 b d
c
▲光折变四波混频过程-实时动态全息
▲用光折变固定技术→高密度光存储 a
∗
▲与一般全息术差别: 2EbEa
i(
kb
−k
a )
Re[
e ]
Δn
∝
2 2
EbEc
∗
| Ea
| + | Eb
|
Ed ∝ E
2 2 a
| Ea
| + | Eb
| →所复现的像不再与被照物严格
2
2
E |
E | + | E |
| a
相似;要求 在横截面上的变化远小于
| a b
219
c
2

§8.8 光折变自泵浦与互泵浦相位共轭
带反射镜的自泵浦相位共轭器
扇形效应(Fanning Effect)
国家自然科学基金委员会
数理学部实验物理讲习班
不带外镜的自泵浦
相位共轭器
1
4
C
A B
2’
3’
2
3
c
图 8.14
(a) 全内反射(TIR) 机制(J.Feinberg)
a
d
z
a
z
=
=
0
0
d
(a)
(b)
z =
图 8.13
z =
L
L
b
c
b
c
220

1
4
图 8.14
2
C
3
221
(b)受激光折变背向散射加四波混频
(SPB-FWM) 机制
国家自然科学基金委员会
数理学部实验物理讲习班
TIR SPB-FWM
的转变
γ
2K
光波长 λ
晶体的掺杂浓度
(C)
C C C
(B)
(A)
图 8.15
γ 2 K

光折变互泵浦相位共轭器
国家自然科学基金委员会
数理学部实验物理讲习班
4
1 1
A
1s
3s
B
3
桥式相位共轭器
4
2
1
3
2
3
1 4 2 3
4
1
C
3
2
222