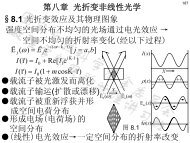
现代光电子学(2)
现代光电子学(2)
现代光电子学(2)
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
第二章 光与物质相互作用基础<br />
2.1 光的吸收<br />
2.2 光的色散和群速色散<br />
2.3 吸收和色散的经典描述<br />
2.4 光在线性介质中的传播<br />
2.5 光在等离子体中的传播<br />
2.6 光场与金属的相互作用和等离激元光学
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
光与物质相互作用现象:<br />
• 弱光 —— 吸收、色散、线性散射<br />
表面等离激元、等离子体共振<br />
(金属、等离子体中 )<br />
• 比较强的光 —— 非线性散射、其它非线性过程<br />
• 强光 —— 非线性吸收、其它非线性过程、<br />
结构改变<br />
• 超强光 —— 多光子电离、隧道电离、<br />
高次谐波
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
Vacuum (or air) Medium<br />
k<br />
n = 1 n = 2<br />
λ<br />
E(x,t) = E 0 exp[i(kx ? ωt)]<br />
2.1 光的吸收<br />
2.1.1 吸收的线性规律<br />
-<br />
线性吸收<br />
λ/n<br />
Absorption depth = 1/ α<br />
nk<br />
Wavelength decreases<br />
- -<br />
E(x,t) = E 0exp[( α/2)x]exp[i(nkx ωt)]
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
I = I 0e<br />
dx<br />
I I -dI<br />
−αl<br />
dI<br />
I<br />
=−αdx<br />
α—— 吸收系数,与光强无关<br />
厚度为 l 的介质层:<br />
I Ie α<br />
l<br />
0<br />
−<br />
= ——朗伯公式<br />
通过厚度为1/α的介质,光强减弱为原来的1/e
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
溶液中, α = AC<br />
C —— 溶液浓度 , A —— 与浓度无关新参数<br />
I Ie −<br />
=<br />
0<br />
ACl<br />
Beer定律<br />
通过吸收测定溶液浓度—— 吸收光谱分析原理
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
2.1.2 复折射率<br />
用折射率表示吸收 —— 复折射率
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
x方向传播单色平面波电场强度<br />
对于吸收介质<br />
Ext % (,) = Axe ()<br />
I( x) = Ie = Ae = A ( x)<br />
−αx 2 −αx<br />
2<br />
0 0<br />
α<br />
i( k+ i ) x<br />
i( kx−ωt) 2 −iωt i( kx % −ωt)<br />
0 0<br />
Ext % ( ,) = Axe ( ) = Ae ⋅ e = Ae<br />
k k i<br />
2<br />
α % = +<br />
k %<br />
—— 复波数<br />
ikx ( −ωt)
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
k<br />
复折射率:<br />
吸收介质中<br />
=<br />
ωn<br />
c<br />
k% ω ω α<br />
= n% = n+ i<br />
c c 2<br />
c<br />
n n i<br />
2<br />
α<br />
% = +<br />
ω<br />
Ext % ( ,) = Ae<br />
0<br />
ω<br />
i( nx % −ωt)<br />
c<br />
将复折射率写成以下形式:<br />
cα<br />
n% = n+ iη η =<br />
2ω<br />
复数 n —— 可以描述吸收的变化<br />
虚部η —— 反应了介质吸收本领
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
2.1.3 吸收与波长的关系<br />
物质材料特性决定透明波段:<br />
大气 300nm — 760nm<br />
石英 180nm — 4000nm<br />
冕玻璃 350nm — 2000nm<br />
火石玻璃 380nm — 2500nm<br />
氟化锂 110nm — 7000nm
补充国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
• 非线性吸收举例<br />
反饱和吸收 双光子吸收
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
第二章 光与物质相互作用基础<br />
2.1 光的吸收<br />
2.2 光的色散和群速色散<br />
2.3 吸收和色散的经典描述<br />
2.4 光在线性介质中的传播<br />
2.5 光在等离子体中的传播<br />
2.6 光场与金属的相互作用和等离激元光学
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
2.2 光的色散和群速色散<br />
2.2.1 色散<br />
l 光在介质中的传播速度(或折射率n)随波<br />
光在介质中的传播速度(或折射率 )随波<br />
长变化而改变的现象 —— 色散 色散<br />
材料n与λ的关系曲线<br />
的关系曲线—— ——色散曲线 色散曲线<br />
l 材料
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
实验表明:在可见光范围,无色透明的介质的<br />
色散曲线形式上都很相似。<br />
基本特征:n随λ的增加而单调下降,在短波端<br />
下降率更大。<br />
dn<br />
0<br />
dλ < dn<br />
0<br />
dω ><br />
或 —— 正常色散
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
1836年 Canchy(科希)给出了一个经验公式:<br />
B C<br />
n= A+ +<br />
λ λ<br />
2 3<br />
A, B, C —— 介质决定的常数,由实验数据给出<br />
当λ变化范围不大时:<br />
B<br />
n= A+ λ<br />
2
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
在强吸收波段:随λ增大n也随之增加<br />
dn<br />
0<br />
dλ > dn<br />
0<br />
dω <<br />
或 —— 反常色散
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
产生色散的原因:所有光学材料的介电响应的内<br />
在频率依赖<br />
结果:波包在色散介质中传播将变宽<br />
引起的问题:<br />
限制信息在光纤中传播的速率<br />
限制锁模激光器中产生脉冲的宽度<br />
限制非线性相互作用<br />
如何克服:<br />
加入负色散光纤<br />
色散补偿<br />
利用各向异性
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
2.2.2 群速色散:群速随波长变化<br />
1 0 1 1 0<br />
现代光通信系统中传输信息的光脉冲
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
单色平面波:<br />
φ = kx−ωt Ext Ae cc<br />
kΔ x= ωΔt<br />
v<br />
p<br />
i( kx−ωt) ( ,) = + ..<br />
相速度 —— 同相位点移动的速度<br />
Δx<br />
ω c<br />
= = =<br />
Δt<br />
k n
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
光脉冲及其傅立叶变换<br />
峰值位置:<br />
同相相加<br />
没有脉冲畸变:<br />
dφ<br />
dω<br />
= 0
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
n( ωω ) x<br />
φ = −ωt<br />
c<br />
v<br />
g<br />
c<br />
=<br />
n+ ωdn/ dω<br />
群折射率<br />
dn<br />
ng= n+<br />
ω<br />
dω<br />
=<br />
dω<br />
dk<br />
无色散时群速等于相速<br />
n ≡ c/ v<br />
g g
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
2.2.3 脉冲畸变<br />
经过正常色散和反常色散介质后脉冲<br />
波形的变化<br />
频<br />
率<br />
随<br />
时<br />
间<br />
改<br />
变<br />
:<br />
啁<br />
啾
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
Train of input telecom pulses<br />
色散导致短脉冲扩展<br />
成为长脉冲。<br />
Many km of fiber<br />
Train of output telecom pulses
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
Long pulse<br />
Short pulse<br />
脉冲和谱
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
脉冲经过色散介质:<br />
L<br />
dispersive<br />
media<br />
ω<br />
1<br />
k( ω) n( ω) k k ( ω ω ) k ( ω ω )<br />
c<br />
2<br />
2<br />
= = 0 + 1 − 0 + 2 − 0 +L<br />
k = k( ω ) 是光脉冲平均的波数<br />
k<br />
k<br />
0 0<br />
1<br />
dk 1 ng<br />
= = =<br />
d v c<br />
ω ω= ω<br />
2 2<br />
0<br />
0<br />
g<br />
2<br />
dk d(1/ vg) 1 dng<br />
= = = 群速的色散参数<br />
dω dω cdω<br />
(GVD parameter)<br />
ω= ω
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
脉冲通过长度为L的介质的渡越时间为 T = L/ v = nL/ c<br />
dT = ( L/ cdn ) g = Lk2dω g g<br />
ΔT ≈ Lk Δω<br />
T 0 为光强下降到1/e时的时间 傅立叶变换得知:<br />
定义色散长度L D 为ΔT = T 0 时介质的长度<br />
Δ T = T = Lk Δ ω = Lk / T<br />
L<br />
D<br />
=<br />
T<br />
k<br />
0 D 2 D 2 0<br />
2<br />
0<br />
2<br />
2<br />
1<br />
Δ ω =<br />
T<br />
L
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
脉冲展宽
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
色散对超短脉冲的影响非常严重!
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
100 fs 1 ps<br />
…<br />
λ 1 λ 2 … λ n<br />
λ 1> λ 2>…> λ n<br />
…<br />
1-m fiber λ n … λ 2 λ 1<br />
1-m fiber<br />
λ 1> λ 2>…> λ n<br />
100 fs
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
利用光栅对做预补偿
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
啁啾镜
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
第二章 光与物质相互作用基础<br />
2.1 光的吸收<br />
2.2 光的色散和群速色散<br />
2.3 吸收和色散的经典描述<br />
2.4 光在线性介质中的传播<br />
2.5 光在等离子体中的传播<br />
2.6 光场与金属的相互作用和等离激元光学
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
经典电磁理论:<br />
经典电磁理论<br />
介质中电子和核将发生位移,形成电偶极子,<br />
并具有一定的固有振动频率ω 并具有一定的固有振动频率 0。<br />
外光场作用下,电偶极子将作受迫阻尼振荡。<br />
频率与外光场的频率相同。<br />
振荡电偶极子形成次级光波,相干叠加的结果<br />
保证了光沿折射方向传播。<br />
Incident light<br />
Emitted light<br />
Transmitted light
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
2.3.1 电介质的洛伦兹模型<br />
洛伦兹的电子论假定:<br />
1. 组成介质的原子或分子内的带电粒子(电子、<br />
离子)被准弹性力保持在它们的平衡位置附<br />
近,并且具有一定的固有振动频率。<br />
2. 在入射光的作用下,介质发生极化,带电粒子<br />
依入射光频率作受迫振动。<br />
3. 原子核(带正电荷)质量大<br />
原子核(带正电荷 )质量大 —— 不动<br />
负电荷相对于正电荷作振动<br />
正、负电荷电量的绝对值相同 —— 电偶极子
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
分子的电偶极矩<br />
p = qr<br />
单位体积平均电偶极矩(极化强度) P = Np =−Ner<br />
电子受迫振动<br />
入射光场为<br />
电子的运动方程<br />
光场强迫力<br />
ω =<br />
0<br />
2<br />
dr dr<br />
=− − −<br />
2<br />
dt dt<br />
m eE fr g<br />
E Ee ω<br />
=<br />
0<br />
f / m<br />
固有振动频率<br />
i t −<br />
准弹性力<br />
阻尼力<br />
γ =<br />
g/ m<br />
阻尼(衰减)系数<br />
eE e<br />
2<br />
−iωt<br />
dr dr 2 0<br />
+ γ + ω<br />
2<br />
0 r =−<br />
dt dt m
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
方程的解<br />
极化强度<br />
rt () =<br />
2<br />
χ = ωp 2 2<br />
( ω0 −ω ) −iγω<br />
( −e)<br />
Ee<br />
m ( ω −ω ) −iγω<br />
−iωt<br />
0<br />
2 2<br />
0<br />
2<br />
Ne Ee<br />
P = N( − er ) = ⋅<br />
m ( ω −ω ) −iγω<br />
P E Ee ω<br />
= εχ = εχ<br />
可以得到电极化率χ的表达式<br />
χ = χ' + iχ"<br />
1<br />
ω −ω<br />
χ'= ω<br />
ω ω γω<br />
2 2<br />
2 0<br />
p<br />
(<br />
2<br />
0 −<br />
2 2<br />
) +<br />
2 2<br />
0 0 0<br />
(复数)<br />
−iωt<br />
0<br />
2 2<br />
0<br />
−i<br />
t<br />
ω<br />
2<br />
p<br />
=<br />
γω<br />
Ne<br />
mε<br />
2<br />
χ" = ωp 2 2 2 2 2<br />
( ω0− ω ) + γω<br />
2<br />
0
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
n%<br />
n<br />
2<br />
+ χ = ε = n = n+ iη<br />
1 n<br />
%<br />
2 2 2 2<br />
n = ( n+ i ) = ( n − ) + i2n 1<br />
= ε = 1+ χ = 1+<br />
ω<br />
( ω −ω ) −iγω<br />
2 2<br />
p<br />
η η η<br />
%<br />
ω −ω<br />
2 2<br />
0<br />
2 2<br />
2 2<br />
− η<br />
2<br />
= 1+<br />
ωp 0<br />
2 2 2 2 2<br />
( ω0− ω ) + γω<br />
2n<br />
γω<br />
2<br />
η = ωp 2 2 2 2 2<br />
( ω0− ω ) + γω
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
n<br />
当原子数密度N不大时 χ
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
具有单一共振频率的介质的色散关系
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
有多个共振频率的情况<br />
f j个电子:ω j、γ j<br />
Z = ∑ f<br />
每个分子的电子 j<br />
j<br />
εω ( ) = 1+<br />
2<br />
Ne '<br />
f<br />
∑ mε ω ω iγω<br />
0<br />
j (<br />
2<br />
j −<br />
j<br />
2<br />
) − j<br />
晶体的透明区域,折射率的半经验Sellmeier公式<br />
n<br />
2<br />
= 1+<br />
∑<br />
A<br />
2<br />
2 2<br />
j j<br />
j<br />
λ<br />
λ − λ
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
f j的另一定义:振子强度<br />
钠原子的能级图<br />
振子强度f(3s → 3p)等<br />
于共振吸收线的强度比<br />
∑<br />
k<br />
I(3s→3 p)<br />
I (3 s→kp) k
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
有多个共振频率的介质的折射率
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
不同原子拥有不同共振频率 w 0, 和线宽, g.
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
分子比原子有更高的态密度,因此吸收谱要<br />
复杂得多<br />
由于吸收有一定的线宽,这些能级可以重叠.<br />
2nd excited<br />
electronic state<br />
1st excited<br />
electronic state<br />
Ground<br />
electronic state<br />
Energy
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
不同玻璃的透射范围<br />
玻璃的吸收<br />
很难找到在波长小于100 nm或波长大于70 μm<br />
处透明的材料.
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
吸收滤光片
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
空气的吸收谱<br />
空气中含有大量的分子,表现出不同的吸收
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
Penetration depth into water (1/α)<br />
1 km<br />
1 m<br />
1 mm<br />
1 µm<br />
Radio Microwave<br />
Wavelength<br />
水的透射谱<br />
随波长的透入深度<br />
IR<br />
UV<br />
1 km 1 m 1 mm 1 µm 1 nm<br />
Visible<br />
spectrum<br />
X-ray<br />
水在可见区透明
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
2.3.2 金属的特鲁德(Drude)模型<br />
自由电子金属<br />
—— 电学和光学性质仅和导带电子有关<br />
自由电子金属<br />
包括碱金属、镁、铝、贵金属<br />
带内跃迁<br />
贵金属<br />
普通金属<br />
带间跃迁
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
特鲁德模型:<br />
1. 只考虑外力对自由的导带电子的影响<br />
2. 宏观的响应是单电子效应乘以电子数----考虑<br />
电子间拥有最强的耦合,即对于微扰所有电子<br />
同相相干响应
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
导带自由电子在单色电磁场作用下的运动方程<br />
介电常数<br />
ω<br />
2<br />
dr dr<br />
γ 2<br />
dt dt<br />
m + m =−eE<br />
e<br />
0<br />
−iωt<br />
2 2 2<br />
ωp ωp ωγ p<br />
εω ( ) = 1− = 1−<br />
+ i<br />
2 2 2 2 2<br />
ω + iγω<br />
ω + γ ωω ( + γ )<br />
p<br />
当ω >> γ时<br />
1<br />
2 2<br />
⎛ ne ⎞<br />
= ⎜ ⎟<br />
⎝ε0m⎠ (特鲁德)等离子体频率<br />
ω<br />
2<br />
p<br />
1( ) ≈1− 2<br />
ε ω<br />
ω<br />
ω = ω p时,ε 1(ω) = 0<br />
2<br />
ωp<br />
ε2( ω) ≈ γ 3<br />
ω
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
自由电子金属的介电常数的实部随频率的变化
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
垂直入射时n型InSb光学反射率的实验值(点)<br />
和理论计算(实线)
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
2.3.3 D和E的关系中的因果性:克喇末<br />
-克朗尼格关系(KK关系)<br />
问题:介质的光学参数都与微观粒子在光场的<br />
作用下的运动有关,那么,光学参数之间有没<br />
有一定的内在联系?<br />
介电常数ε(ω)的实部和虚部的关系 —— KK关系
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
单脉冲响应:假设系统是线性的,对于复杂的随时间<br />
变化的场的响应,可以由脉冲响应的叠加来构建。<br />
t = 0时刻短时间间隔dt、E → Edt (场脉冲)<br />
X(t):脉冲响应<br />
极化强度EX(t)dt<br />
对t = 0时刻单位脉冲(Edt = 1)的响应<br />
因果律要求:X(t) = 0 ( t < 0)
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
求一般的场E(t)所产生的极化强度<br />
t = 0时刻的脉冲 → X(t)<br />
t′时刻的脉冲E(t′)dt′ →X(t-t′)<br />
t时刻的极化强度,为t时刻前所有脉冲响应叠加:<br />
Pt () = ∫ Et (') Xt ( −t')<br />
dt '<br />
根据因果律,t时刻之后的脉冲响应为零<br />
即t – t′
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
单色场<br />
E E exp( i t)<br />
ω =<br />
0<br />
∞<br />
0<br />
Pt () = E exp( iωtX ) ( t−t') dt '<br />
∫<br />
−∞<br />
∞<br />
iωt i t"<br />
Ee ∫<br />
− ω<br />
0 e Xt dt E<br />
−∞<br />
= (") " = χω ( )<br />
D= εεω ( ) E = ε E+ P<br />
0 0<br />
[ ]<br />
ε0 εω ( ) − 1 = χω ( )<br />
(利用 t″≡t -t′)<br />
极化率<br />
也是X(t)的傅立叶变换
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
dt ()<br />
为了求得KK关系,利用单位阶跃函数<br />
⎧⎪ limexp( st) ( : 1), whent < 0;<br />
s→0<br />
= ⎨<br />
⎪⎩ 0 whent≥0. 此单位阶跃函数的傅立叶变换<br />
D( ω) lim( s iω)<br />
−<br />
= −<br />
s→0<br />
由于X(t) = 0 ( t < 0),则<br />
1<br />
X() tdt () = 0 对此式进行傅立叶变换:<br />
χω ( ) ∗ D(<br />
ω)<br />
= 0<br />
0<br />
D(t)<br />
1<br />
t
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
1.<br />
2.<br />
∞ χω ( ')<br />
0 = χω ( ) ∗ D( ω) = lim∫ dω'<br />
s→0<br />
−∞ s−i( ω−ω') ∞ εω ( ') −1<br />
= ε0lim∫ dω'<br />
s→0<br />
−∞ s−i( ω−ω') 将积分分为两部分:1. ω - s → ω + s;2. 其余部分。<br />
ω+ s εω ( ') −1<br />
ω+<br />
s dω'<br />
lim∫ dω'<br />
= [ εω ( ) −1]<br />
∫<br />
s→0ω−s<br />
s−i( ω−ω') ω−s<br />
s−i( ω−ω') [ ( ) 1]<br />
ε(ω′)为常数 = π εω−<br />
(结果与s无关)<br />
(<br />
ω s<br />
) ω s<br />
− ∞ εω ( ') −1 ∞ εω ( ') −1<br />
lim ∫ + ∫ dω'≡P∫ dω'<br />
s→0−∞<br />
+ s−i( ω−ω') -∞−i(<br />
ω−ω') 主部
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
实部:<br />
虚部:<br />
1 ( ') 1<br />
( ) 1 '<br />
( ') d<br />
∞ εω −<br />
εω = + P∫<br />
ω<br />
π −∞ i ω−ω ε(ω) = ε 1(ω) + iε 2(ω)<br />
εω ε ω<br />
1 ε ( ω')<br />
ε ω ω<br />
π ( ω−ω') *<br />
( ) = ( − )<br />
∞<br />
2<br />
1(<br />
) = 1+ P∫<br />
d '<br />
−∞<br />
2 ∞ ωε ' 2(<br />
ω')<br />
= 1+ P∫<br />
dω'<br />
0 2 2<br />
π ( ω −ω')<br />
1 ε ( ω')<br />
−1<br />
ε ω ω<br />
π ( ω−ω') ∞<br />
1<br />
2(<br />
) =− P∫<br />
d '<br />
−∞<br />
=−<br />
2<br />
ωε [ ( ω')<br />
−1]<br />
dω<br />
( ')<br />
∞<br />
1 P∫0<br />
2 2<br />
π ω −ω<br />
'<br />
KK关系
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
n<br />
η<br />
洛伦兹模型:<br />
ω ω ω<br />
= 1+<br />
⋅<br />
2 ( )<br />
2<br />
p<br />
2<br />
0 −<br />
2<br />
2 2<br />
ω0− ω<br />
2 2 2<br />
+ γω<br />
2<br />
ωp γω<br />
= ⋅<br />
2 ( ω − ω ) + γ ω<br />
2<br />
0<br />
2 2 2 2<br />
KK关系
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
补充<br />
超光速传播<br />
V = c
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
在非吸收区群速小于相速<br />
vg = c 0 / (n n + ω dn/dω) dn/d<br />
在正常色散区 dn/dw是正的,<br />
dn/d 是正的,vg < c
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
在反常色散区群速可以超过真空光速<br />
vg = c 0 / (n n + ω dn/dω) dn/d<br />
在反常色散区dn<br />
在反常色散区 dn/dω为负 为负, , 也就是在近共振时,v 也就是在近共振时, g 可以超过<br />
可以超过c 0<br />
问题:1. 吸收非常强;2. 共振区通常很窄,只有在一<br />
个很窄的区域有v g > c 0,超出这个频率范围 v g < c 0,<br />
光脉冲(具有较宽的频谱)将分裂变形。
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
超光速实验<br />
条件:1. 在一个比较大的频率范围内获得负的<br />
dn/dω;<br />
2. 在这个范围内吸收要小,群速色散小。<br />
方法:利用光脉冲产生增益(代替吸收),使色散<br />
曲线反转,在两个共振峰之间可以获得小的<br />
吸收和近线性的负斜率。
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
吸收<br />
2<br />
增益
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
铯蒸气中增益协助超光速传播<br />
Gain-assisted superluminal light propagation<br />
Nature 406 (2000, July, 20 ) 277, L.J. Wang et. al.<br />
λ = 852 nm, Δn = -1.8 × 10 -6 , Δν = 1.9 MHz<br />
理论值:<br />
dn<br />
ng= n+<br />
ω =−332.6<br />
dω
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
3.7 μs脉冲光通过介质—— 6 cm铯蒸气<br />
E 1,E 2 存在时与不存在时通过介质的时间差为 t -t 0 = -62±1ns<br />
实验值: n<br />
g<br />
c L/ t t +Δt 0.2−62 v L/( t +Δt)<br />
t 0.2<br />
0 0<br />
= = = = =−<br />
g<br />
0 0<br />
309
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
第二章 光与物质相互作用基础<br />
2.1 光的吸收<br />
2.2 光的色散和群速色散<br />
2.3 吸收和色散的经典描述<br />
2.4 光在线性介质中的传播<br />
2.5 光在等离子体中的传播<br />
2.6 光场与金属的相互作用和等离激元光学
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
麦克斯韦方程<br />
物质方程<br />
波动方程<br />
2.4 光在线性介质中的传播<br />
∂B<br />
∇ × E = −<br />
∂t<br />
∇ ⋅ D = 0<br />
D ε E + P = εE<br />
= 0<br />
2<br />
2 ∂E ∂ E<br />
∇ E−σμ<br />
− εμ = 2<br />
∂t ∂t<br />
2<br />
2 ∂B ∂ B<br />
∇ B−σμ<br />
− εμ = 2<br />
∂t ∂t<br />
∂D<br />
∇ × H = +<br />
∂t<br />
∇ ⋅ B = 0<br />
J<br />
B = μH<br />
J = σE<br />
线性极化<br />
0<br />
0
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
方程解可以表达为简谐平面波之和:<br />
E= E<br />
0<br />
e<br />
代入波动方程:<br />
i( kr ⋅ −ωt)<br />
2 2 2<br />
k ( i )<br />
ω<br />
B = B<br />
0<br />
e<br />
i( kr ⋅ −ωt)<br />
2 2<br />
− k + iσμω+ εμω =<br />
σ<br />
σ<br />
= ωμε + = ωμε εω= ( ε + i )<br />
ω<br />
ω<br />
复波矢的虚部等于α/2:<br />
0<br />
复介电常数<br />
2<br />
1<br />
2<br />
1<br />
2<br />
⎧ ⎡ ⎤⎫<br />
⎪1 ⎛ σ ⎞ ⎪<br />
α = 2ω εμ ⎢ 1 1⎥<br />
⎨ + −<br />
2 2<br />
2 ⎢⎜ ⎟ ⎬<br />
⎝ ωε ⎠<br />
⎥<br />
⎪ ⎢ ⎥⎪<br />
⎩ ⎣ ⎦⎭<br />
2/α为透入深度 —— 电场衰减为原来的1/e
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
第二章 光与物质相互作用基础<br />
2.1 光的吸收<br />
2.2 光的色散和群速色散<br />
2.3 吸收和色散的经典描述<br />
2.4 光在线性介质中的传播<br />
2.5 光在等离子体中的传播<br />
2.6 光场与金属的相互作用和等离激元光学
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
2.5 光在等离子体中的传播<br />
d<br />
m e<br />
dt =−<br />
略去离子的运动和磁场的作用,电子的运动方程为:<br />
v<br />
E<br />
考虑单色平面波<br />
σ<br />
E= E<br />
0<br />
e<br />
i( kr ⋅ −ωt)<br />
e i( ⋅ −ωt)<br />
e<br />
=− ∫<br />
kr E<br />
v E0<br />
e dt =<br />
m imω<br />
等离子体中的传导电流密度:<br />
电导率:<br />
2<br />
ne e =−<br />
imω<br />
ne<br />
2<br />
J =− ne e v=− e E<br />
imω<br />
n e :单位体积内的电子数目
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
等离子体是电中性的(ρ = 0),由麦克斯韦方程得:<br />
2<br />
2 ω σ<br />
k i ω<br />
2 2<br />
c ε0c<br />
− + + =<br />
k<br />
ω<br />
1<br />
= ( ω −ω<br />
)<br />
c<br />
2 2 2<br />
2<br />
p<br />
2<br />
p<br />
=<br />
2<br />
ne e<br />
ε m<br />
0<br />
其中等离子体的ε、μ近似为ε 0 、μ 0<br />
0<br />
ω p 称为等离子体频率
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
k<br />
1<br />
= ( ω −ω<br />
)<br />
c<br />
2 2 2<br />
2<br />
p<br />
1. 当ω < ω p 时,k 2 < 0,k为一纯虚数。<br />
光场的透入深度为<br />
3. 等效介电常数<br />
2<br />
σ ω p<br />
εω= ε0 + i = ε0(1<br />
− ) 2<br />
ω ω<br />
δ<br />
=<br />
2<br />
c<br />
ω −ω<br />
2 2<br />
p<br />
2. 当ω > ω p时,k为实数,这是光场可以在其中传播<br />
当ω > ω p时<br />
n = εω/ ε0<br />
< 1
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
第二章 光与物质相互作用基础<br />
2.1 光的吸收<br />
2.2 光的色散和群速色散<br />
2.3 吸收和色散的经典描述<br />
2.4 光在线性介质中的传播<br />
2.5 光在等离子体中的传播<br />
2.6 光场与金属的相互作用和等离激元光学
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
2.6 光场与金属的相互作用和等离激元光学<br />
(Plasmonics)<br />
2.6.1 表面等离激元(surface plasmon, SP)<br />
介质-金属界面的表面等<br />
离激元的电磁场<br />
表面电荷分布
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
介质1<br />
介质2<br />
麦克斯韦方程<br />
H<br />
E<br />
H<br />
E<br />
E = E<br />
x1 x2<br />
H = H<br />
y1 y2<br />
ε E = εω ( ) E<br />
x1 z1<br />
(;) xt (0, H ,0) e<br />
=<br />
1 y1<br />
ik ( x+ k z−ωt) x1 z1<br />
( xt ;) = ( E ,0, E ) e<br />
1 x1 z1<br />
x2 z2<br />
(;) xt (0, H ,0) e<br />
=<br />
2 y2<br />
i( k x+ k z−ωt) ik ( x+ k z−ωt) x2 z2<br />
( xt ;) = ( E ,0, E ) e<br />
2 x2 z2<br />
μ<br />
t<br />
∂H<br />
∇× E =−<br />
∂<br />
i( k x+ k z−ωt) ∂D<br />
∇× H =<br />
∂t<br />
∇⋅ D=∇⋅ H= 0 D= εE<br />
边界条件: 电场切向连续<br />
1 z1 z2<br />
磁场切向相等(传导电流为零)<br />
电位移矢量法向相等(面电荷<br />
密度为零)
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
k = k = k<br />
电场切向连续导致波矢相同: x1 x2 x<br />
ωε Ex1 = kz1Hy1 ωε Ex2 = kz2Hy2 kz1 kz2<br />
= 表面等离激元存在的条件<br />
ε εω ( )<br />
1<br />
与z有关的相位因子:<br />
e<br />
ik z<br />
电场沿z方向指数衰减:k zi为纯虚数<br />
介质1中: ik z1z < 0, z > 0<br />
介质2中: ik z2z < 0, z < 0<br />
1 z<br />
1<br />
2
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
k<br />
由波动方程得:<br />
2 2 ⎛ω⎞ kx + kzi<br />
= ε i⎜<br />
⎟<br />
⎝ c ⎠<br />
1/2<br />
k<br />
ω⎛<br />
=<br />
εεω ( ) ⎞<br />
= k<br />
⎝ ⎠<br />
1<br />
x ⎜ ⎟ sp<br />
c ε1+ εω ( )<br />
εω ( ) = ε' + iε"<br />
ω⎛<br />
εε'<br />
⎞<br />
≈ ⎜ ⎟<br />
⎝ε + ε ' ⎠<br />
' 1<br />
sp<br />
c 1<br />
1/2<br />
传播长度:L p = 1/k sp″<br />
k<br />
k = k + ik<br />
2<br />
' "<br />
sp sp sp<br />
" 1<br />
sp<br />
c 1<br />
3/2<br />
ω ⎛ εε'<br />
⎞ ε"<br />
≈ ⎜ ⎟<br />
⎝ε + ε '⎠ 2ε' 对于Ag,630 nm,ε′ = -18, ε″ = 0.5, L p = 119 μm<br />
2
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
求z方向的穿透深度:<br />
穿透深度:<br />
2 2 2<br />
2 ⎛ω ⎞ 2 ⎛ω⎞ ⎛ω ⎞ 1<br />
z1 = ε1⎜ ⎟ − x = ε1⎜<br />
⎟ −⎜<br />
⎟<br />
⎝ c ⎠ ⎝ c ⎠ ⎝ ⎠ 1<br />
k k<br />
L<br />
L<br />
z1<br />
z2<br />
⎛ω⎞ = ⎜ ⎟<br />
⎝ c ⎠<br />
2 2<br />
ε1<br />
ε + ε<br />
c ε<br />
εε'<br />
+ ε '<br />
对于Ag,600 nm,L z1 = 390 nm, L z2 = 24 nm<br />
2<br />
1<br />
1 ⎛ω⎞ -ε1−ε ' λ -ε1−ε '<br />
= = ⎜ ⎟ =<br />
k ⎝ c ⎠ ε 2π<br />
ε<br />
z1<br />
1 1<br />
1<br />
= =<br />
k<br />
z2<br />
λ -ε1−ε '<br />
2π −ε'<br />
'
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
2.6.2 光场和表面等离激元的耦合<br />
光场和表面等离激元的色散 实验配置
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
Otto结构示意图<br />
两种模式:TM 有sp模;TE 无sp模
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
动量匹配示意图
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
实验装置
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
入射光的反射率随入射角的变化<br />
p偏振和s偏振入射光的反射率随入射角的变化
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
Kretschmann结构示意图
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
2π sinθ<br />
λ<br />
光栅衍射激发<br />
k = k ± nG ± mG<br />
k<br />
sp x x y<br />
x<br />
=<br />
x y<br />
a0x a0y<br />
入射光在x方向的波数<br />
2π 2π<br />
G = , G = 光栅的波数
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
其它激发方式<br />
近场探针激发 粗糙表面的激发
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
补充 等离激元共振<br />
相干共振<br />
在中世纪已经用来做彩<br />
色玻璃<br />
不同尺寸的<br />
金纳米球
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
补充<br />
等离激元的重要性<br />
• 光和等离激元之间可以互相转化<br />
• 电子的德布罗意波长远小于光的波长<br />
• 等离激元电磁场的空间局域<br />
• 场增强
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
银膜上的周期性小孔<br />
几何结构<br />
2 2<br />
kxi j 2 π / a0<br />
电镜照片<br />
= + a 0:空间周期;i, j:散射级次<br />
k c i j a<br />
2 2<br />
sp = εmεd /( εm + εd) ω/ = + 2 π /<br />
0
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
超透明小孔实验结果<br />
透过的光是打到小孔上的光的两倍<br />
实验条件<br />
银膜厚:200nm<br />
小孔直径:150nm<br />
光栅周期:900nm<br />
按小孔衍射理论计算<br />
的透过率:0.1%
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
周期:<br />
300,450,550 nm<br />
小孔直径:<br />
155,180,225 nm<br />
透过峰值波长:<br />
436,538,627 nm
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
牛眼型SP结构(2002年,Science)<br />
Free standing film<br />
60 nm
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
产生纳米光
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
SP波导
国家自然科学基金委员会<br />
数理学部实验物理讲习班<br />
SP传感器