III. ERDVĖS ANALIZINĖ GEOMETRIJA

Apskritimo (1) lygtį galime užrašyti dar ir taip
2 2 2 ( a + b − ) = 0
2 2
x + y − 2ax
− 2by
+ r .
Bendroji antrojo laipsnio lygtis yra
2
2
Ax + Bxy + Cy + Dx + Ey + F = 0 . (3)
Lygtis (3) reiškia apskritimą tada, kai A = C ir kai B = 0 . Kai abi šios sąlygos yra
patenkintos, gauname antrojo laipsnio lygties atskirą atvejį
arba
2 2
Ax + Ay + Dx + Ey + F = 0
(4)
2 2 D E F
x + y + x + y + = 0 .
A A A
Paskutiniosios lygties narius sugrupuojame ir gauname
2
© A.Laurutis, D.Šiaučiūnas Analizinė geometrija 52
2
2 2
⎛ D ⎞ ⎛ E ⎞ D + E − 4 AF
⎜ x + ⎟ + ⎜ y + ⎟ =
(5)
2
⎝ 2 A ⎠ ⎝ 2 A ⎠ 4 A
D
Palyginame (1) ir (5) lygtis ir matome, kad a = − , b
2 A
D + E − 4 AF
= .
4 A
2 2
Apskaičiuojame r
2
E
−
2 A
D + E − 4 AF
= .
4 A
2 2
=
2
ir r
2
Galimi trys atvejai, suprantama, kai A ≠ 0 :
2 2
1. D + E − 4 AF > 0 , tada r yra tikrasis skaičius ir lygtis (5) yra apskritimo lygtis.
2 2
2. D + E − 4 AF = 0 , tada r = 0 ir lygtis (5) yra nulinio spindulio apskritimo lygtis– taškas.
2 2
3. D + E − 4 AF < 0 , tada r yra menamasis skaičius, o lygtis (5) –menamo apskritimo
lygtis.
( c,
0)
F −
1
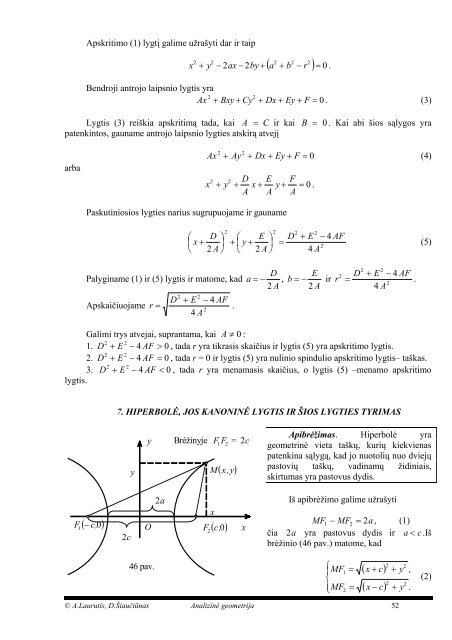
7. HIPERBOLĖ, JOS KANONINĖ LYGTIS IR ŠIOS LYGTIES TYRIMAS
2 c
y
y
O
46 pav.
2 a
Brėžinyje F F = 2c
F
2
M
x
1
2
( x,
y)
( c,
0)
x
Apibrėžimas. Hiperbolė yra
geometrinė vieta taškų, kurių kiekvienas
patenkina sąlygą, kad jo nuotolių nuo dviejų
pastovių taškų, vadinamų židiniais,
skirtumas yra pastovus dydis.
Iš apibrėžimo galime užrašyti
MF1 − MF2
= 2a
, (1)
čia 2 a yra pastovus dydis ir a < c .Iš
brėžinio (46 pav.) matome, kad
⎧
⎪MF1
=
⎨
⎪⎩ MF2
=
( x + c)
( x − c)
2
2
+ y
2
+ y
2
,
.
(2)