Op extensie belaste staaf Opgave 2 - TU Delft

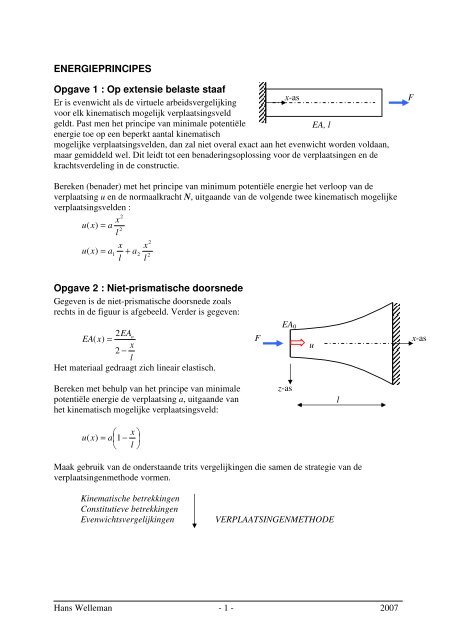
ENERGIEPRINCIPES
Opgave 1 : Op extensie belaste staaf
Er is evenwicht als de virtuele arbeidsvergelijking
voor elk kinematisch mogelijk verplaatsingsveld
x-as F
geldt. Past men het principe van minimale potentiële
energie toe op een beperkt aantal kinematisch
EA, l
mogelijke verplaatsingsvelden, dan zal niet overal exact aan het evenwicht worden voldaan,
maar gemiddeld wel. Dit leidt tot een benaderingsoplossing voor de verplaatsingen en de
krachtsverdeling in de constructie.
Bereken (benader) met het principe van minimum potentiële energie het verloop van de
verplaatsing u en de normaalkracht N, uitgaande van de volgende twee kinematisch mogelijke
verplaatsingsvelden :
2
x
u(
x)
= a 2
l
2
x x
u(
x)
= a1
+ a2
2
l l
Opgave 2 : Niet-prismatische doorsnede
Gegeven is de niet-prismatische doorsnede zoals
rechts in de figuur is afgebeeld. Verder is gegeven:
2EAo
EA(
x)
=
x
2 −
l
Het materiaal gedraagt zich lineair elastisch.
Bereken met behulp van het principe van minimale
potentiële energie de verplaatsing a, uitgaande van
het kinematisch mogelijke verplaatsingsveld:
⎛ x ⎞
u( x)
= a⎜1
− ⎟
⎝ l ⎠
Maak gebruik van de onderstaande trits vergelijkingen die samen de strategie van de
verplaatsingenmethode vormen.
Kinematische betrekkingen
Constitutieve betrekkingen
Evenwichtsvergelijkingen VERPLAATSINGENMETHODE
Hans Welleman - 1 - 2007
F
EA0
z-as
u
l
x-as

Opgave 3 : Uitkragende ligger
Bepaal met behulp van het principe van minimale potentiële energie het verloop van de
zakking w, het buigend moment
M en de dwarskracht V,
F
uitgaande van het kinematisch
mogelijke verplaatsingsveld :
B
2
x
w ( x)
= a
A
l
Vergelijk de resultaten met het
(bekende) exacte verloop.
l
2
Opgave 4 : Uitkragende ligger (vervolg)
Kies voor de ligger uit de vorige opgaven als verplaatsingsveld:
2 3
x x x
w( x)
= ao
+ a1
+ a2
+ a 2 3 3
l l l
a) Is dit verplaatsingsveld kinematisch mogelijk? Zo niet, pas het dan aan.
b) Bereken met het principe van minimale potentiële energie het verloop van de zakking
w.
Opgave 5 : Op extensie belaste staaf (2)
Van de in de figuur weergegeven constructie is de
verplaatsing bij de opleggingen verhinderd. Op de
prismatische kolom met rekstijfheid EA werkt over
de lengte l een gelijkmatig verdeelde belasting q.
Het normaalkrachtenverloop in de kolom wordt
berekend met de strategie van de
verplaatsingenmethode. Voor de verplaatsingen
u(x) in de x-richting wordt het volgende verloop
aangenomen :
∧ πx
∧
u( x)
= u sin amplitude u
l
z-as
De amplitude van deze sinusfunctie is een nog
nader te bepalen constante.
Vragen:
a) Toon aan dat het gekozen verplaatsingsveld voldoet aan de kinematische
randvoorwaarden.
b) Bereken de amplitude, uitgedrukt in q, l en EA, met behulp van het principe van
minimum potentiële energie.
c) Teken de bijbehorende N-lijn en schrijf de waarden er bij ( met de goede tekens! ).
Hans Welleman - 2 - 2007
l
q
EA
x
u(x)
x-as

Opgave 1 : Op extensie belaste staaf
De potentiële energie kan worden bepaald op basis van het aangenomen verplaatsingsveld dat
voldoet aan de randvoorwaarden en daardoor een kinematisch toelaatbaar verplaatsingsveld
is. Voor verplaatsingveld en rek geld :
2
ax
u = 2
l
du
2ax
ε = = 2
dx
l
De potentiële energie is nu te schrijven als:
l
1 2
V = ∫ 2 EA×
ε dx − F × a = ∫
0
2EAa
V =
3l
2
− Fa
l
0
1
2
⎛ 2ax
⎞
EA×
⎜ ⎟ dx − F × a
2
⎝ l ⎠
Een stabiel evenwicht is alleen mogelijk indien bij een kleine variatie van de
toestandsvariabele de verandering van de potentiële energie nul is. De toestandsvariabel is in
dit geval a. Dit houdt wiskundig in dat moet gelden :
dV
δ V = δa
= 0
da
Dit moet gelden voor iedere, kinematisch mogelijke variatie van de toestandsvariabele. Dat
betekent dat de variatie van de potentiële energie alleen nul kan zijn indien de afgeleide van
de potentiële energie naar de toestandsvariabele nul is:
dV
= 0
da
Dit is het principe van minimale potentiële energie. Uitwerken levert:
dV
4EAa
= − F = 0
da
3l
3 Fl
a =
4 EA
⇔
Het benaderde verplaatsingsveld is zodoende:
u ( x)
=
3 FL
4 EA
x
l
2
2
De potentiële energie heeft hiermee een (negatieve waarde) van :
V
2
− 3 F l
=
8 EA
Hans Welleman - 3 - 2007
2
⇔

Opgave 2 : Niet-prismatische doorsnede
De potentiële energie kan worden bepaald op basis van het aangenomen verplaatsingsveld dat
voldoet aan de randvoorwaarden en daardoor een kinematisch toelaatbaar verplaatsingsveld
is. Op basis van dit verplaatsingsveld is de rek :
du
− a
ε = =
dx
l
De potentiële energie is nu te schrijven als:
l
1 2
V = ∫ 2 EA(
x)
× ε dx − F × a
0
De rekstijfheid is nu geen constante maar een gegeven functie van de plaats x en kan dus niet
buiten de integraal worden gehaald. Netjes uitwerken levert voor de totale potentiële energie:
l
l
2EAo
a
− EA
1 ⎛ − ⎞
o 2 1 ⎛ x ⎞
V = ∫ 2 × × ⎜ ⎟ dx − Fa = a d⎜
− ⎟ − Fa
x ⎝ l ⎠
l ∫ 2
x ⎝ l
0 2 −
0 2 −
⎠
l
l
− EAo
V = a
l
2
2
⎡ x ⎤
⎢
ln( 2 −
l ⎥
⎣ ⎦
l
0
EA
− Fa =
l
o
a
2
− Fa
Een stabiel evenwicht is alleen mogelijk indien bij een kleine variatie van de
toestandsvariabele de verandering van de potentiële energie nul is. De toestandsvariabel is in
dit geval a. Dit houdt wiskundig in dat moet gelden :
dV
δ V = δa
= 0
da
Dit moet gelden voor iedere, kinematisch mogelijke variatie van de toestandsvariabele. Dat
betekent dat de variatie van de potentiële energie alleen nul kan zijn indien de afgeleide van
de potentiële energie naar de toestandsvariabele nul is:
dV
= 0
da
Hans Welleman - 4 - 2007
ln 2
Dit is het principe van minimale potentiële energie. Uitwerken levert:
dV
2EAo
=
da
l
1
a =
2ln
2
Fl
EA
ln 2
o
− F = 0
⇔

Opgave 3 : Uitkragende ligger
De potentiële energie kan worden bepaald op basis van het aangenomen verplaatsingsveld dat
voldoet aan de randvoorwaarden en daardoor een kinematisch toelaatbaar verplaatsingsveld
is. Op basis van dit verplaatsingsveld is de kromming :
κ =
2
d w 2a
− = 2 2
dx
l
De potentiële energie is nu te schrijven als:
V
=
l
∫
0
1
2
2
EI × κ dx − F × a =
l
∫
0
1
2
⎛ 2a
⎞
EI × ⎜ ⎟ dx − F × a
2
⎝ l ⎠
Netjes uitwerken levert voor de totale potentiële energie:
2
2EIa
V = − Fa
3
l
Een stabiel evenwicht is alleen mogelijk indien bij een kleine variatie van de
toestandsvariabele de verandering van de potentiële energie nul is. De toestandsvariabel is in
dit geval a. Dit houdt wiskundig in dat moet gelden :
dV
δ V = δa
= 0
da
Dit moet gelden voor iedere, kinematisch mogelijke variatie van de toestandsvariabele. Dat
betekent dat de variatie van de potentiële energie alleen nul kan zijn indien de afgeleide van
de potentiële energie naar de toestandsvariabele nul is:
dV
= 0
da
Dit is het principe van minimale potentiële energie. Uitwerken levert:
dV
4EIa
= − F = 0
3
da
l
3
Fl
a =
4EI
⇔
De potentiële energie heeft hiermee een (negatieve waarde) van :
V
2
− F l
=
8 EI
3
Hans Welleman - 5 - 2007
2

Opgave 4 : Uitkragende ligger (vervolg)
Een kinematisch mogelijk verplaatsingsveld heeft bij de inklemming een zakking en
hoekverdraaiing nul. Een toelaatbaar verplaatsingveld en de daarbij behorende kromming
zijn:
2 3
x x
w = a2
+ a 2 3 3
l l
2
d w 2a2
6a3
x
κ = − = − −
2
2 3
dx
l l
De potentiële energie is nu te schrijven als:
V
l
= ∫
0
1
2
2
EI × κ dx − F × ( a
2
3
3
6EIa
V =
l
6EIa2
a
+ 3
l
3
2
2EIa
+ 3
l
+ a ) =
3
2
2
− F ×
( a + a )
Een stabiel evenwicht is alleen mogelijk indien bij een kleine variatie van de
toestandsvariabele de verandering van de potentiële energie nul is. De toestandsvariabelen
zijn in dit geval a2 en a3. Dit houdt wiskundig in dat moet gelden :
dV
dV
δ V = δa2
+ δa
da
da
2
3
3
= 0
Dit moet gelden voor iedere, kinematisch mogelijke variatie van de toestandsvariabelen. Dat
betekent dat de variatie van de potentiële energie alleen nul kan zijn indien de beide
afgeleiden van de potentiële energie naar de toestandsvariabelen nul zijn:
dV
da
2
= 0
en
dV
da
3
= 0
Dit is het principe van minimale potentiële energie. Uitwerken levert:
dV
da
2
dV
da
3
6EIa
= 3
l
3
12EIa
= 3
l
3
4EIa
+ 3
l
2
6EIa
+ 3
l
2
− F = 0
− F = 0
Dit levert twee vergelijkingen met twee onbekenden. De onbekenden a2 en a3 en het
verplaatsingveld w(x) zijn hiermee :
a
2
3
Fl
= ;
2EI
a
3
3
Fl
= − ;
6EI
⇒
Hans Welleman - 6 - 2007
2
2 3
Flx Fx
w(
x)
= −
2EI
6EI
De potentiële energie heeft hiermee een (negatieve waarde) van :
V
2
− F l
=
6 EI
3
3

Opgave 5 : Op extensie belaste staaf (2)
De potentiele energie vergelijking luidt:
l l
1
∫ 2
2
ε ∫
0 0
V = EA× dx − q × u dx
2
2
1 π ̂ 2 π x ̂ π x
V = 2 EA u cos dx q u sin dx
2
l ∫ − ×
l ∫ l
2
π 2
̂ 2ql
1 V = EA u − û
4
l π
2
dV ̂ ⎛ π 1 ̂ 2ql
⎞
δV = δ u = EA u δ û
0
̂ ⎜ − 2
⎟ =
du ⎝ l π ⎠
2
̂ 4ql
u = 3
π EA
l l
0 0
Of hiermee de potentiele energie een minimum of een maximum bereikt kan worden
onderzocht door naar de 2 e afgeleide te kijken:
d V
dû
π
EA
l
2 2
2
1 = 2 2 > 0
Hiermee is aangetoond dat het extreem een minimum betreft.
Hans Welleman - 7 - 2007