Neliniarități ale comportamentului materialelor

Capitolul 3
NELINIARITĂŢI ALE COMPORTAMENTULUI MATERIALELOR
- II-
3.3.3. Schematizarea curbelor caracteristice ale materialelor
Aşa cum s-a afirmat deja, unul din principalele obiective ale teoriei plasticităţii îl
reprezintă stabilirea unor relaţii între tensiuni şi deformaţii specifice. Acest lucru este posibil
pe baza analizei comportamentului materialului la diferite teste de laborator. Comportamentul
în domeniul plastic al unei structuri dintr-un anumit material, care în mod uzual este rezultatul
unei stări complexe (multiaxiale) de tensiuni, este analizat pe baza rezultatelor unui test
uniaxial (la tracţiune sau la compresiune), efectuat pe o epruvetă din acel material.
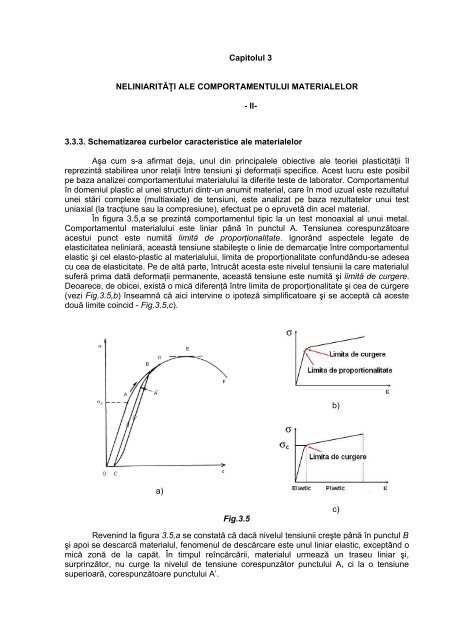
În figura 3.5,a se prezintă comportamentul tipic la un test monoaxial al unui metal.
Comportamentul materialului este liniar până în punctul A. Tensiunea corespunzătoare
acestui punct este numită limită de proporţionalitate. Ignorând aspectele legate de
elasticitatea neliniară, această tensiune stabileşte o linie de demarcaţie între comportamentul
elastic şi cel elasto-plastic al materialului, limita de proporţionalitate confundându-se adesea
cu cea de elasticitate. Pe de altă parte, întrucât acesta este nivelul tensiunii la care materialul
suferă prima dată deformaţii permanente, această tensiune este numită şi limită de curgere.
Deoarece, de obicei, există o mică diferenţă între limita de proporţionalitate şi cea de curgere
(vezi Fig.3.5,b) înseamnă că aici intervine o ipoteză simplificatoare şi se acceptă că aceste
două limite coincid - Fig.3.5,c).
b)
a)
Fig.3.5
c)
Revenind la figura 3.5,a se constată că dacă nivelul tensiunii creşte până în punctul B
şi apoi se descarcă materialul, fenomenul de descărcare este unul liniar elastic, exceptând o
mică zonă de la capăt. În timpul reîncărcării, materialul urmează un traseu liniar şi,
surprinzător, nu curge la nivelul de tensiune corespunzător punctului A, ci la o tensiune
superioară, corespunzătoare punctului A’.

Cu alte cuvinte, deformaţiile plastice au condus la o creştere a limitei de curgere a
materialului. Se spune că materialul s-a ecruisat. Termenul de ecruisare trebuie înţeles ca o
creştere a limitei de curgere a materialului.
Rigiditatea materialului, caracterizată de modulul de elasticitate, fie rămâne
nemodificată, aşa cum se întâmplă în timpul fazelor de încărcare şi descărcare ale testului,
fie se diminuează, ca atunci când epruveta ajunge din A în B. În timpul reîncărcării, după
începerea curgerii în A’, se tinde către parcurgerea curbei iniţiale ABDE către punctul D
(dacă materialul nu ar fi fost descărcat în B, s-ar fi parcurs curba ABDE). Aceasta
demonstrează o trăsătură remarcabilă a comportamentului materialului: la descărcarea în B,
materialul „păstrează în memorie ” evenimentele trecute şi, mai mult decât atât,
evenimentele „memorate” influenţează deformaţiile ulterioare. Cu alte cuvinte,
comportamentul în domeniul plastic este influenţat de toată „istoria” anterioară procesului
studiat (de „drumul” parcurs, începând cu starea nedeformată şi netensionată).
Când tensiunea depăşeşte valoarea corespunzătoare punctului D, materialul
continuă să se „întărească” până la atingerea valorii maxime a tensiunii, corespunzătoare
punctului E. Din acest moment, materialul fie curge plastic la un nivel constant al tensiunii fie
suferă un proces de „înmuiere”, caracterizat prin deteriorarea proprietăţilor sale de rezistenţă
şi de rigiditate, pâna la cedare (rupere), în punctul F (Fig.3.5,a).
Din cele prezentate mai sus rezultă că pentru procesele legate de apariţia
deformaţiilor plastice încetează să mai fie valabilă corespondenţa biunivocă tensiunideformaţii
specifice (caracteristică fenomenelor elastice, liniare şi neliniare). Chiar şi în
procesul simplu al întinderii uniaxiale deformarea la un moment dat depinde nu numai de
valoarea tensiunii „actuale” ci şi de valorile tuturor tensiunilor anterioare care au acţionat
asupra epruvetei, începând cu starea sa iniţială („naturală”). Aceasta este diferenţa esenţială
dintre comportamentul elastic şi cel plastic al unui material.
Un model matematic care să caracterizeze comportamentul plastic trebuie să conţină
anumiţi „parametri de memorie” care să permită trasarea „drumului” deformaţiilor plastice
(tensiuni, deformaţii specifice sau combinaţii ale acestora). Cu cât numărul acestor parametri
este mai mare, cu atât modelul matematic este mai performant.
Pentru a putea formula un model de calcul pentru o stare complexă de solicitare
pornind de la rezultatele unui test uniaxial (curba din Fig.3.5,a) un prim pas îl reprezintă
„idealizarea„ relaţiei tensiuni-deformaţii specifice, de exemplu ca in figura 3.6. Se poate
observa că s-a neglijat bucla de histerezis, considerând că descărcarea şi reîncărcarea se
produc pe acelaşi traseu (BC identic cu CA) şi s-a omis faza de „înmuiere”- EF.
Examinând curba idealizată, se pot remarca câteva aspecte esenţiale, necesare pentru
formularea unui model de calcul corect în domeniul deformaţiilor plastice:
• Criteriul de plasticitate (Funcţia de plasticitate)
Se impune necesitatea generalizării conceptului de curgere din cazul unei solicitări
uniaxiale. Astfel se ajunge la conceptul de funcţie de plasticitate. În spaţiul cu 9
dimensiuni al tensorului tensiunilor, o funcţie de curgere reprezintă o hipersuprafaţă,
reprezentând frontiera dintre două tipuri de stări de tensiune:
- cea închisă de suprafaţa de curgere, care include orice stare de tensiuni
care poate fi atinsă fără a induce deformaţii plastice suplimentare în
material;
- cea din exteriorul acestei suprafeţe, care cuprinde acele stări de tensiuni
care induc deformaţii plastice suplimentare în material.
Pe baza funcţiei de plasticitate se poate formula un criteriu de plasticitate care ne
furnizează informaţii dacă se produc sau nu deformaţii plastice atunci când materialul este
supus unei combinaţii de variaţii de tensiune pe diferite direcţii.

Fig.3.6
• Legea de curgere
Pe curba idealizată din figura 3.6 se consideră un punct oarecare, B. Atunci când se
atinge valoarea tensiunii corespunzătoare acestui punct, materialul s-a deformat
elastic cu cantitatea e
ε şi a curs plastic cu cantitatea p
ε .
Deformaţia specifică totală se obţine prin însumarea deformaţiei specifice elastice cu
cea plastică, astfel:
e p
ε = ε + ε
(3.25)
În domeniul elastic, pentru calculul deformaţiilor specifice pentru orice combinaţie de
tensiuni, sunt folosite relaţiile din Teoria elasticităţii. Pentru deformaţiile plastice este
necesară o lege de curgere.
• Legea de întărire
Pe măsură ce materialul se întăreşte (ecruisează), funcţia de curgere se schimbă. Ca
urmare sunt necesare funcţii (legi) care să descrie ce se întâmplă cu materialul supus
unei stări de solicitare complexă, după depăşirea zonei de curgere (similar
fenomenului de „întărire” la testul uni-axial).
În concluzie, în cazul solicitării elasto-plastice relaţia generală între tensiuni şi
deformaţii specifice trebuie să conţină:
1. Relaţiile între tensiuni şi deformaţii specifice în domeniul elastic.
2. Un criteriu de plasticitate, care să indice începutul curgerii plastice.
3. Legea de curgere.
4. Legea de întărire/înmuiere (descrierea comportamentului după începerea curgerii
până la cedare).
OBSERVAŢIE
Este necesar să se facă o precizare cu consecinţe importante pentru calculul în
domeniul elasto-plastic. Pentru o solicitare în domeniul elastic se poate folosi curba
caracteristică convenţională, trasată pe baza valorilor convenţionale ale tensiunilor şi
deformaţiilor specifice, calculate pe baza ariei iniţiale a secţiunii transversale a epruvetei şi a
lungimii iniţiale a acesteia (Vezi relaţiile 2.1 şi 2.2, Cap.2):
F ∆ l
σ = ; ε = . (3.26)
A 0 l 0
Această curbă nu poate evidenţia deformaţia specifică reală a unui material.

Caracteristica reală (Fig.3.7) se poate trasa pe baza valorilor instantanee ale
dimensiunilor epruvetei (Relaţiile 2.4 şi 2.5, Cap.2). Între valorile convenţionale şi cele reale
există relaţiile stabilite în Capitolul 2:
r = σ ( 1 ε ) ; ε = ln( 1 + ε )
σ +
r (3.27)
Caracteristica reală furnizează tensiunile necesare pentru ca materialul să se deformeze
plastic la o anumită valoare a deformaţiei specifice şi de aceea este cunoscută şi sub
denumirea de curbă de curgere.
O ecuaţie matematică care aproximează cu suficientă exactitate această curbă, din
momentul începerii curgerii până la sarcina maximă corespunzătoare gâtuirii (fig.3.7,b), este
o funcţie exponenţială de forma:
n
σ = Kε , (3.28)
unde K este valoarea tensiunii la care ε = 1 iar n este exponentul de ecruisare (panta
reprezentării în coordonate logaritmice a ecuaţiei (3.28).
a) b)
Fig.3.7
Modelele matematice utilizate în teoria plasticităţii sunt deosebit de complexe. Pentru
simplificare se recurge la schematizarea curbei caracteristice σ = f ( ε ) , având pe toate
porţiunile ei expresii analitice cât mai simple dar, în acelaşi timp, fiind cât mai apropiată de
curba caracteristică reală. Pe baza acestor diagrame schematizate calculul de rezistenţă
poate fi condus prin metode analitice.
Se disting două feluri de schematizări: prin linii drepte şi prin linii curbe.
Schematizările prin linii drepte se folosesc în special în cazul materialelor care în domeniul
elastic satisfac legea lui Hooke.
În figura 3.8 se prezintă câteva schematizări mai des utilizate prin linii drepte.
Notând cu ε c deformaţia specifică corespunzătoare limitei de curgere, pentru un
material elasto-plastic (cu o caracteristică reală de forma celei din figura 3.7,b) se poate
adopta schematizarea prin două drepte din figura 3.8,a.
Ecuaţiile celor două drepte sunt:
• pentru domeniul deformaţiilor elastice, pe care este valabilă legea lui Hooke,
σ = Eε pentru 0 < ε < ε c , (3.29)
unde E este modulul de elasticitate longitudinal al materialului (panta dreptei OA):
E = tan β , (3.30)

• pentru domeniul deformaţiilor elasto-plastice,
unde
σ
( ε − )
= σ c + E p
ε c , pentru ε c
ε > , (3.31)
E p = tan β 1 , (3.32)
este modulul de plasticitate - panta dreptei AE, prin care se poate exprima, cu excepţia unor
scurte intervale pe care raportul d σ /dε
are variaţii brusce, curba reală ABE. De regulă, E p
este mult mai mic decât E.
Schematizarea din figura 3.8,a se poate utiliza în cazul materialelor care au
deformaţii elastice şi zonă de ecruisare. Celelalte schematizări sunt cazuri particulare ale
schematizării descrise mai sus.
Schematizarea din Fig.3.8,b este cunoscută sub numele de schematizarea lui Prandtl
şi se referă la materialele ideal elasto-plastice. Această schematizare, care conduce la
rezultate suficient de precise în cazul oţelurilor cu un conţinut redus de carbon şi al
aluminiului, consideră că materialul nu se întăreşte după depăsirea limitei de curgere. De
asemenea, nu se limitează lungimea dreptei orizontale din diagramă, având ecuaţia
σ = σ . (3.33)
c
Rezultă că în cazul materialelor ideal elasto-plastice modulul de plasticitate se
consideră nul ( E p = 0 ).
Dacă deformaţiile elastice sunt neglijabile în comparaţie cu cele plastice, se pot
adopta schematizările din Fig.3.8c – d. În aceste cazuri E → ∞ şi materialul se consideră
rigid până la limita de curgere şi apoi plastic. Dacă prezintă întărire se numeşte rigido-plastic
(Fig.3.8,c) iar dacă palierul de curgere are lungime mare, ideal rigido-plastic (Fig.3.8,d).
a) b)
c) d)
Fig.3.8
În cazul unor materiale care nu satisfac legea lui Hooke, se adoptă schematizări prin
linii curbe, de regulă funcţii exponenţiale de forma (3.1).
Consideraţiile de mai sus sunt aplicabile nu numai în cazul stărilor liniare de tensiune,
adică între tensiuni normale σ şi deformaţii specifice liniare ε, ci şi în cazul stărilor de
forfecare pură, adică între tensiuni tangenţiale τ şi lunecările specifice, γ.