4. Lagrange-Formalismus
4. Lagrange-Formalismus
4. Lagrange-Formalismus
Erfolgreiche ePaper selbst erstellen
Machen Sie aus Ihren PDF Publikationen ein blätterbares Flipbook mit unserer einzigartigen Google optimierten e-Paper Software.
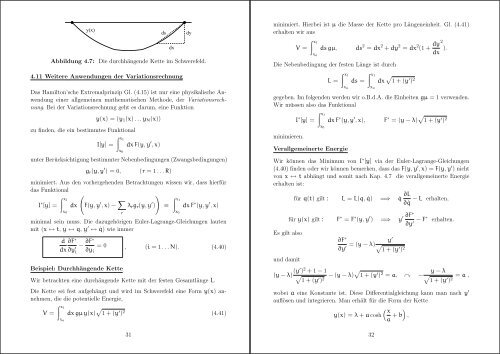
y(x)<br />
Abbildung <strong>4.</strong>7: Die durchhängende Kette im Schwerefeld.<br />
<strong>4.</strong>11 Weitere Anwendungen der Variationsrechnung<br />
Das Hamilton’sche Extremalprinzip Gl. (<strong>4.</strong>15) ist nur eine physikalische Anwendung<br />
einer allgemeinen mathematischen Methode, der Variationsrechnung.<br />
Bei der Variationsrechnung geht es darum, eine Funktion<br />
y(x) = (y1(x) . . . yN(x))<br />
zu finden, die ein bestimmtes Funktional<br />
I[y] =<br />
x1<br />
x0<br />
dx F(y, y ′ , x)<br />
unter Berücksichtigung bestimmter Nebenbedingungen (Zwangsbedingungen)<br />
ds<br />
gr(y, y ′ ) = 0, (r = 1 . . . R)<br />
minimiert. Aus den vorhergehenden Betrachtungen wissen wir, dass hierfür<br />
das Funktional<br />
I ∗ <br />
x1<br />
[y] = dx F(y, y ′ , x) − <br />
λrgr(y, y ′ <br />
) ≡<br />
x1<br />
dx F ∗ (y, y ′ , x)<br />
x0<br />
r<br />
minimal sein muss. Die dazugehörigen Euler-<strong>Lagrange</strong>-Gleichungen lauten<br />
mit (x ↔ t, y ↔ q, y ′ ↔ ˙q) wie immer<br />
d ∂F<br />
dx<br />
∗<br />
∂y ′ i<br />
− ∂F∗<br />
∂yi<br />
Beispiel: Durchhängende Kette<br />
= 0 , (i = 1 . . . N). (<strong>4.</strong>40)<br />
Wir betrachten eine durchängende Kette mit der festen Gesamtlänge L.<br />
Die Kette sei fest aufgehängt und wird im Schwerefeld eine Form y(x) annehmen,<br />
die die potentielle Energie,<br />
V =<br />
x1<br />
xo<br />
dx gµ y(x) 1 + (y ′ ) 2 (<strong>4.</strong>41)<br />
31<br />
dx<br />
x0<br />
dy<br />
minimiert. Hierbei ist µ die Masse der Kette pro Längeneinheit. Gl. (<strong>4.</strong>41)<br />
erhalten wir aus<br />
V =<br />
x1<br />
xo<br />
ds gµ, ds 2 = dx 2 + dy 2 = dx 2 (1 + dy<br />
2<br />
).<br />
dx<br />
Die Nebenbedingung der festen Länge ist durch<br />
L =<br />
x1<br />
xo<br />
ds =<br />
x1<br />
xo<br />
dx 1 + (y ′ ) 2<br />
gegeben. Im folgenden werden wir o.B.d.A. die Einheiten gµ = 1 verwenden.<br />
Wir müssen also das Funktional<br />
minimieren.<br />
I ∗ [y] =<br />
x1<br />
x0<br />
Verallgemeinerte Energie<br />
dx F ∗ (y, y ′ , x), F ∗ = (y − λ) 1 + (y ′ ) 2<br />
Wir können das Minimum von I ∗ [y] via der Euler-<strong>Lagrange</strong>-Gleichungen<br />
(<strong>4.</strong>40) finden oder wir können bemerken, dass das F(y, y ′ , x) = F(y, y ′ ) nicht<br />
von x ↔ t abhängt und somit nach Kap. <strong>4.</strong>7 die verallgemeinerte Energie<br />
erhalten ist:<br />
Es gilt also<br />
und damit<br />
für q(t) gilt : L = L(q, ˙q) =⇒ ˙q ∂L<br />
− L erhalten,<br />
∂ ˙q<br />
für y(x) gilt : F ∗ = F ∗ (y, y ′ ′ ∂F∗<br />
) =⇒ y<br />
∂y ′ − F∗ erhalten.<br />
∂F∗ y<br />
= (y − λ)<br />
∂y ′ ′<br />
<br />
1 + (y ′ ) 2<br />
(y − λ) (y′ ) 2 + 1 − 1<br />
<br />
1 + (y ′ ) 2 − (y − λ)1 + (y ′ ) 2 y − λ<br />
= a, − = a ,<br />
1 + (y ′ ) 2<br />
wobei a eine Konstante ist. Diese Differentialgleichung kann man nach y ′<br />
auflösen und integrieren. Man erhält für die Form der Kette<br />
<br />
x<br />
<br />
y(x) = λ + a cosh + b ,<br />
a<br />
32