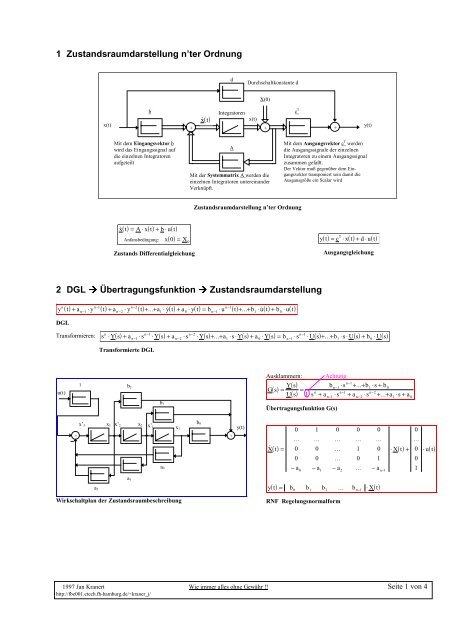
Zustandsraumdarstellung n'ter Ordnung

1 Zustandsraumdarstellung n’ter Ordnung
d
b
Integratoren
xt ()
x(t)
x(t) y(t)
+ + +
Mit dem Eingangsvektor b
wird das Eingangssignal auf
die einzelnen Integratoren
aufgeteilt
xt () = A⋅ xt () + b⋅ut ()
x(
) = X
Anfansbedingung: 0 0
Zustands Differentialgleichung
A
1997 Jan Kranert Wie immer alles ohne Gewähr !! Seite 1 von 4
http://fbe001.etech.fh-hamburg.de/~kraner_j/
X(0)
Mit der Systemmatrix A werden die
einzelnen Integratoren untereinander
Verknüpft.
Durchschaltkonstante d
Zustandsraumdarstellung n’ter Ordnung
2 DGL Übertragungsfunktion Zustandsraumdarstellung
n
n−1
n−2
n−1
y () t + a ⋅ y () t + a ⋅ y () t + ... + a ⋅ y() t + a ⋅ y() t = b ⋅ u () t + ... + b ⋅ u() t + b ⋅u()
t
DGL
n−1
n−2
1 0 n−1
1 0
c T
Mit dem Ausgangsvektor c T werden
die Ausgangssignale der einzelnen
Integratoren zu einem Ausgangssignal
zusammen gefaßt.
Der Vektor muß gegenüber dem Eingangsvektor
transponiert sein damit die
Ausgansgröße ein Scalar wird
T
yt () = c ⋅ xt () + d⋅ ut ()
Ausgangsgleichung
n
n−1
n−2
n−1
Transformieren: s ⋅ Y( s) + a ⋅s ⋅ Y( s) + a ⋅s ⋅ Y( s) + ... + a ⋅s⋅ Y( s) + a ⋅ Y( s) = b ⋅s ⋅ U( s) + ... + b ⋅s⋅ U( s) + b ⋅U(
s)
u(t)
+
1
x’3
a2
n−1
Transformierte DGL
x3
x’2
b2
a1
x2
x’1
b1
a0
n−2
Wirkschaltplan der Zustandsraumbeschreibung
x1
b0
1 0 n−1
+
y(t)
1 0
Ausklammern: Achtung
n−1
Ys ( ) bn−1⋅ s + ... + b1⋅ s+ b0
Gs ( ) = = n
n−1
n−
2
Us ( ) 1⋅
s + a ⋅ s + a ⋅ s + ... + a ⋅ s+ a
n−1
Übertragungsfunktion G(s)
n−2
1 0
0 1 0 0 0
0
... ... ... ... ... ...
Xt () = 0 0 ... 1 0 ⋅ Xt () + 0 ⋅ut
()
0 0 ... 0 1
0
−a −a −a ... −a
1
0 1 2 n−1
yt () = b b b ... b ⋅Xt
()
0 1 2 n−1
RNF Regelungsnormalform

3 Übertragungsglieder
3.1 I-Glied
Symbol Übertragun
gsfunktion
Gs ( )
=
K I
s
Betragsgang Phasengang Bodediagramm
( ω)
Gj
3.2 PT1-Glied
Symbol Übertragungsfunktion Betragsgang
Phasengang
Gs ()
K P
=
1 + Ts
3.3 PTt-Glied
Symbol Übertragungsfunktion
()
Gs e Ts t = −
=
K I
ω
( ω)
Gj
ϕ(jω) = -90° ω=KI
K P
=
2
1 + ( Tω)
( j ) =−arctan ( T )
ϕ ω ω
3.4 PT2-Glied
Symbol Übertragungsfunktion Betragsgang
Phasengang
0 < ϑ < ∞
ϑ = 1
Gs ( )
( ω)
Gj
K P
=
1+ 2ϑTs
+ T s
K P
= 2
1 + ( Tω)
Pole : 1
2
s12
, = [ − ϑ± ϑ −1]
h(t)
1
-1/T1 -1/T2
T
ϑ > 1
Im
Re
t
2 2
( ω)
Gj
=
K P
2 [ 1− ( Tω) ] + 4(
ϑTω) 2
− 2ϑTω
ϕ( jω)
= arctan
2
1−
( Tω)
( j ) =−2arctan ( T )
ϕ ω ω
h(t)
1
-1/T
ϑ > 1
-20dB/dek
Seite 2 von 4 Wie immer alles ohne Gewähr !! 1997 Jan Kranert
http://fbe001.etech.fh-hamburg.de/~kraner_j/
⏐G(ω) ⏐
ω = 1
⏐G(ω) ⏐
-20dB/dek
KI [dB]
ω= 1
T
Betragsgang Phasengang
Gjω ( ) =1 ( )
2
( ω)
Gj
=
⏐G(ω) ⏐
ϕ jω =− Ttω -40dB/dek
K
ω= 1
T
ω
Bodediagramm
ω
0°
-45°
-90°
Bodediagramm
ω
0°
-90°
-180°
ϕ(ω)
ϕ(ω)
ϕ(ω)
-90°
ω= 1
T
ω= 1
T
P
2
2 ϕ( jω) =−arctan( T1ω) −arctan(
T2ω)
[ 1+ ( T1ω) ] [ 1+
( T2ω)
]
ϑ = 1 ϑ < 1 ϑ = 0
Im
Doppelpol
Re
t
h(t)
1
-1/T
Im
1 2
1 −ϑ
T
Re
1
− 1−ϑ
T
2
t
h(t)
1
j
T
− j
T
Im
Re
t
ω
ω
ω

3.5 PI-Glied
Symbol Übertragungsfunktion Betragsgang
Phasengang
K I
Gs () = KR
+
s
K I
= ( 1+
Ts N )
s
K R
Gs () = ( 1+
Ts N )
Ts N
K R
TN
=
K I
3.6 PDTR-Glied
2
2 K I
Gj ( ω)
= KR
+
ω
K I
2
= ( TNω
) + 1
ω
1
ϕ( jω)
=−arctan
TNω
= arctan(
TNω
) − 90°
Symbol Übertragungsfunktion Betragsgang
Phasengang
Gs ( )
K K s
Ts
K K
Ts K s
R + D
=
1+
R
R
D
= 1+
1+
R
R
( ω)
Gj
=
= K
+ ( ω)
2
( T ω)
2
K K
R
R D
1+
R
K D
1+
ω
K R
2
1+
( T ω)
K
ϕ ω ω Rω
K
D
( j ) = arctan − arctan(
T )
R
-20dB/dek
Bodediagramm
1997 Jan Kranert Wie immer alles ohne Gewähr !! Seite 3 von 4
http://fbe001.etech.fh-hamburg.de/~kraner_j/
R
2
2
⏐G(ω) ⏐
KR
ω= 1
T N
KI * KR
⏐G(ω) ⏐
KR
ω
0°
-45°
-90°
ϕ(ω)
Bodediagramm
K
T
D
R
ω= 1
T R
-20dB/dek
ω= 1
T
ω= K
K
Wird das PDTR-Glied als Regler verwendet sollte TR sehr viel kleiner als dir kleinste Zeitkonstante der Strecke sein: T ≈ T
1
10
3.7 PIDTR-Glied
Symbol
Übertragungsfunktion
Betragsgang
Phasengang
Bodediagramm
D
R
ω
R min( strecke )
K
Gs ( ) K K s
s
Ts
K K K
s
s( T s)
K K s
I
1
= R + + D ⋅
1+
R
I R D 2
= 1+
+
1+
R
I I
2
2 K I
KR + KDω−
ω
Gj ( ω)
=
2
1+
( TRω
)
K D K I
ϕ( jω)
= arctan ω−
− arctan(
TRω
)
K R K Rω
ω= K
K D
⏐G(ω) ⏐
TR
KDKI 1
ω=
KDKI I
K D
Wird das PIDTR-Glied als Regler verwendet, sollte TR sehr viel kleiner als dir kleinste Zeitkonstante der Strecke sein: T ≈ T
1
10
4 Hurwitz
Maßgebend für das Hurwitzkriterium ist das Nennerpolynom des geschlossenen Regelkreises.
Ist das Hurwitzkriterium erfüllt, kann der Regelkreis als stabil angesehen werden.
Alle Koeffizienten des Nennerpolynoms müssen größer als Null sein.
Zusätzlich: Bei dritter Ordnung: aa 1 2− aa 0 3> 0
Bei vierter Ordnung: aa 3 2− aa 1 4> 0
2 2
aaa 3 2 1−aa 0 3−
aa 4 1 >
0
ω
ω= K K
D I
R min( strecke )
ω

5 Reglersynthese
5.1 Statische Genauigkeit
Die statische Genauigkeit hängt von dem I-Verhalten des offenen Kreises und der Eingangsgröße ab.
Das I-Verhalten des Kreises läßt sich aus folgender Form ablesen:
2
K 1+
as 1 + as 2 + ... + ams GO( s)
= l ⋅
2
s 1+
bs+ bs + ... + b s
1 2
m
n −1
n −1
⋅ e
−
Ts
t
Für den Endwert der Regelabweichung bei Führungs- oder Störgrößenanregung ergibt sich:
et () et ()
=
wt () zt ()
Proportionales
Verhalten
Integrales
Verhalten
Doppelt Integrales
Verhalten
Sprung
1
1+ K0
0
0
Rampe
∞
1
0
Parabel
∞
Seite 4 von 4 Wie immer alles ohne Gewähr !! 1997 Jan Kranert
http://fbe001.etech.fh-hamburg.de/~kraner_j/
K 0
(K 0 = Verstärkung des offenen Kreises)
5.2 Kompensationsverfahren
Mit Hilfe bestimmter Reglertypen lassen sich die Pole der Regelstrecke kompensieren („wegkürzen“).
Kompensiert wird natürlich der offene Regelkreis.
Die Nullstelle eines PDTR-Regelgliedes kann einen Pol der Regelstrecke kompensieren:
K K
Ts K s
R
D KP
KRKP 1+ ⋅ =
1+
1+ Ts 1+
Ts
R
R
1
R
∞
K
wenn T R =
K
Die beiden Nullstellen eines PIDTR-Regelgliedes können zwei Pole der Strecke kompensieren:
s
K K K
s
T s
K s
K
T K
I
R D 2
1+ + ⋅
+ R
+
R
2 KD
wenn: 2ϑ
1 = und T1
=
K
K
KK
2 2
( 1+
) KI I 1 2ϑTs 1 T1 s s( 1 + T s)
I
I
=
D
R
P I P
R
5.3 Vorgabe der Phasenreserve ΨR
Die Phasenreserve ist die Differenz der Phase des offenen Kreises zu 180° bei ωD (Durchtrittskreisfrequenz), der Frequenz
bei der der Betragsgang gleich 1 wird.
Die Dimensionierung des Regelkreises bei vorgegebener Phasenreserve ΨR wird in den folgenden Schritten durchgeführt:
!
ϕ ω = ϕ ω + ϕ ω = Ψ − 180 °
1. Berechnung der Durchtrittskreisfrequenz aus gegebenem Phasenwinkel: O( D) R( D) S( D) R
G ( jw ) G ( jw ) G ( jw )
2. Berechnung der Verstärkung, meist KI oder KR, damit die Verstärkung
des offenen Kreises bei ωD gleich 1 wird:
Zusätzlich bei PI-Regler: meist ist TN = 10
ω
D
0 Proportionales Verhalten
für dir Konstante l gilt: 1 Integrales Verhalten
2 Doppelt Integrales Verhalten
gefordert. Daraus folgt der konstante Phasenwinkel des Reglers: ϕ ( ω )
1
K 0
= + =1
!
O D R D S D
R D =− 5, 711°