Darstellung komplexer Zahlen in der Polarform
Darstellung komplexer Zahlen in der Polarform
Darstellung komplexer Zahlen in der Polarform
Sie wollen auch ein ePaper? Erhöhen Sie die Reichweite Ihrer Titel.
YUMPU macht aus Druck-PDFs automatisch weboptimierte ePaper, die Google liebt.
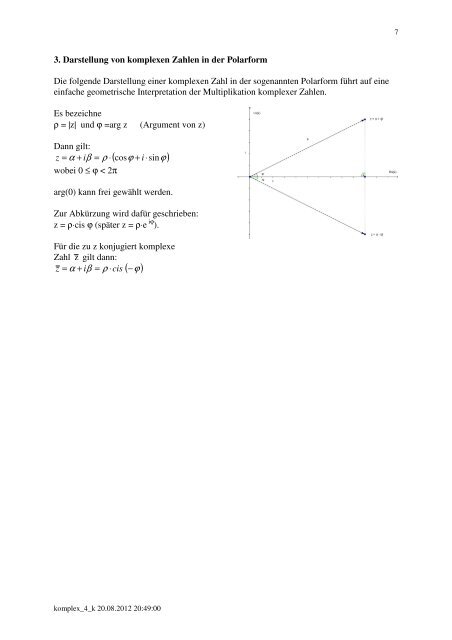
3. <strong>Darstellung</strong> von komplexen <strong>Zahlen</strong> <strong>in</strong> <strong>der</strong> <strong>Polarform</strong><br />
Die folgende <strong>Darstellung</strong> e<strong>in</strong>er komplexen Zahl <strong>in</strong> <strong>der</strong> sogenannten <strong>Polarform</strong> führt auf e<strong>in</strong>e<br />
e<strong>in</strong>fache geometrische Interpretation <strong>der</strong> Multiplikation <strong>komplexer</strong> <strong>Zahlen</strong>.<br />
Es bezeichne<br />
ρ = |z| und ϕ =arg z (Argument von z)<br />
Dann gilt:<br />
z = α + iβ<br />
= ρ ⋅(<br />
cosϕ + i ⋅s<strong>in</strong><br />
ϕ)<br />
wobei 0 ≤ ϕ < 2π<br />
arg(0) kann frei gewählt werden.<br />
Zur Abkürzung wird dafür geschrieben:<br />
z = ρ⋅cis ϕ (später z = ρ⋅e iϕ ).<br />
Für die zu z konjugiert komplexe<br />
Zahl z gilt dann:<br />
z<br />
= α + iβ<br />
= ρ ⋅cis<br />
−ϕ<br />
( )<br />
komplex_4_k 20.08.2012 20:49:00<br />
7
Es gelten die folgenden<br />
Umrechnungsformeln:<br />
<strong>Polarform</strong> → Normalform<br />
Re z = ρ cos ϕ<br />
Im z = ρ s<strong>in</strong> ϕ<br />
Beispiel:<br />
z = 8 cis 135°<br />
= 8 ⋅ cos135°<br />
+ is<strong>in</strong>135°<br />
= −2<br />
+ 2<br />
Normalform → <strong>Polarform</strong><br />
komplex_4_k 20.08.2012 20:49:00<br />
( ) i<br />
Beispiele zur Vorbereitung:<br />
3 = 3 cis 0° i = cis 90° − 5 = 5 cis π<br />
− 1+ i = 2 cis 135 °<br />
(halbes Quadrat)<br />
− 1+ 3i = 2 cis 120°<br />
(halbes gleichseitiges Dreieck)<br />
Allgeme<strong>in</strong>:<br />
2 2<br />
z = α + iβ ≠ 0 ρ = α + β<br />
Das Argument ϕ ist so zu bestimmen, dass gilt:<br />
Im ( z)<br />
Re(<br />
z)<br />
s<strong>in</strong> ϕ = und cos ϕ =<br />
z<br />
z<br />
Variante:<br />
Im ( z)<br />
Falls Re (z) ≠ 0<br />
tanϕ<br />
=<br />
Re(<br />
z)<br />
wobei <strong>in</strong> diesem Fall abzuklären ist, <strong>in</strong> welchen Quadrant z liegt.<br />
z = 3 - 4i = 5 cis 306.9° (4. Quadrant)<br />
z = -3i = 3 cis 270°<br />
8
4. Multiplikation <strong>komplexer</strong> <strong>Zahlen</strong> <strong>in</strong> <strong>der</strong> <strong>Polarform</strong><br />
z = ρ ⋅ cisϕ<br />
1 1 1<br />
z = ρ ⋅ cisϕ<br />
2 2 2<br />
( ρ ϕ ) ( ρ ϕ ) ρ ρ ( ϕ s<strong>in</strong>ϕ ) ( ϕ s<strong>in</strong>ϕ<br />
)<br />
ρ ρ ( cosϕ cosϕ s<strong>in</strong>ϕ s<strong>in</strong>ϕ ) i(<br />
s<strong>in</strong>ϕ cosϕ cosϕ s<strong>in</strong>ϕ<br />
)<br />
z ⋅ z = ⋅cis ⋅ ⋅ cis = ⋅ ⋅ cos + i ⋅ cos + i<br />
1 2 1 1 2 2 1 2 1 1 2 2<br />
komplex_4_k 20.08.2012 20:49:00<br />
( )<br />
= ⋅ ⋅ ⋅ − ⋅ + ⋅ + ⋅<br />
1 2 1 2 1 2 1 2 1 2<br />
Mit den Additionstheoremen für s<strong>in</strong> und cos ergibt sich schliesslich:<br />
( cos( ) s<strong>in</strong> ( ) ) ( )<br />
z ⋅ z = ρ ⋅ ρ ⋅ ϕ + ϕ + i ϕ + ϕ = ρ ⋅ ρ ⋅ cis ϕ + ϕ<br />
1 2 1 2 1 2 1 2 1 2 1 2<br />
das heisst:<br />
Komplexe <strong>Zahlen</strong> werden multipliziert, <strong>in</strong>dem man ihre Beträge multipliziert und ihre<br />
Argumente addiert.<br />
z z = z ⋅ z<br />
1<br />
⋅ und arg( z ⋅ z ) = arg(<br />
z ) + arg(<br />
z )<br />
2<br />
1<br />
2<br />
1<br />
2<br />
1<br />
Die Multiplikation e<strong>in</strong>er komplexen Zahl mit ρ cis ϕ bedeutet also geometrisch e<strong>in</strong>e<br />
Drehstreckung mit dem Faktor ρ und dem Drehw<strong>in</strong>kel ϕ.<br />
Beispiele:<br />
(3 + 3i) (5 2 cis 135°) = (3 2 cis 45°)⋅(5 2 cis 135°) = 30 cis 180° = -30<br />
1<br />
z = 1+<br />
i = 2cis45°<br />
z = ( 1+<br />
i 3)<br />
= cis 60°<br />
1<br />
2<br />
2<br />
Wegen z ⋅ z = 2 cis 105°<br />
erhält man durch Multiplikation <strong>in</strong> <strong>der</strong> Normalform den genauen<br />
1<br />
2<br />
2(<br />
1+<br />
3)<br />
Wert für s<strong>in</strong>105<br />
=<br />
° und analog cos 105°<br />
4<br />
Das Produkt zweier <strong>komplexer</strong> <strong>Zahlen</strong> kann geometrisch ermittelt werden. Dazu betrachtet<br />
man ähnliche Dreiecke:<br />
Beispiel:<br />
z1 = 1.5 + 0.4i = 1.55 cis 14.9°<br />
z2 = 1.1 + 0.8i = 1.36 cis 36.0°<br />
z1z2 = 2.11 cis 50.9°<br />
Der absolute Betrag ρ des Produkts<br />
ρ = ρ1⋅ρ2 kann als Verhältnisgleichung<br />
ρ ρ1<br />
geschrieben werden: =<br />
ρ 1<br />
2<br />
2<br />
9
Multipliziert man <strong>in</strong>sbeson<strong>der</strong>e e<strong>in</strong>e komplexe Zahl mit cis ϕ, so bedeutet dies e<strong>in</strong>e Drehung<br />
mit Zentrum O um den W<strong>in</strong>kel ϕ. Damit können die Abbildungsgleichungen e<strong>in</strong>er Drehung<br />
um den Nullpunkt leicht hergeleitet werden.<br />
Drehung des Punktes P(z = x + iy) um den Nullpunkt<br />
(x + iy) cis ϕ = (x + iy) (cos ϕ + i s<strong>in</strong>ϕ) = (x cos ϕ - y s<strong>in</strong> ϕ) + i(x s<strong>in</strong> ϕ + y cosϕ)<br />
Kontrolle: die Bil<strong>der</strong> <strong>der</strong> Basisvektoren stehen aufe<strong>in</strong>an<strong>der</strong> senkrecht (Skalarprodukt!). Damit<br />
heissen die Abbildungsgleichungen:<br />
x´ = x cos ϕ - y s<strong>in</strong> ϕ<br />
y´ = x s<strong>in</strong> ϕ + y cos ϕ<br />
Aufgabe:<br />
Das Dreieck ABC ist gleichseitig. Bestimme die<br />
dritte Ecke C <strong>in</strong> den folgenden Fällen:<br />
a) A(0), B(4 + i) C<br />
b) A(2 + i), B(4 + 5i)<br />
a)<br />
C geht aus B durch e<strong>in</strong>e 60°-Drehung um den<br />
Nullpunkt hervor.<br />
z = z ⋅ cis 60° = z ⋅ cos 60° + is<strong>in</strong><br />
60°<br />
C B B<br />
( 4 1 i) ( 2 i<br />
3<br />
2 )<br />
1<br />
2<br />
1 ( 2 )<br />
= + ⋅ + ⋅<br />
komplex_4_k 20.08.2012 20:49:00<br />
( )<br />
= 2 − ⋅ 3 + i ⋅ + 2⋅ 3 ≈ 1.13+ 3.96i<br />
b)<br />
Tipp: Der Vektor AC geht aus dem Vektor AB durch e<strong>in</strong>e 60° Drehung hervor.<br />
Übungsaufgabe:<br />
Berechne z so, dass das Dreieck A(1), B(z) C(z 2 ) rechtw<strong>in</strong>klig-gleichschenklig mit rechtem<br />
W<strong>in</strong>kel bei A ist.<br />
10
Insbeson<strong>der</strong>e bedeutet die Multiplikation mit i e<strong>in</strong>e 90°-Drehung im Gegenuhrzeigers<strong>in</strong>n.<br />
E<strong>in</strong>e schöne Anwendung dazu ist die folgende Denksportaufgabe des Physikers Gamov<br />
(Spektrum 10.1979)<br />
E<strong>in</strong>e alte Urkunde berichtet von e<strong>in</strong>em Piratenschatz, <strong>der</strong> auf e<strong>in</strong>er verlassenen Insel<br />
vergraben wurde und erklärt, wie man den Schatz wie<strong>der</strong>f<strong>in</strong>den kann. Auf <strong>der</strong> Insel stehen nur<br />
zwei Bäume, A und B, und die Reste e<strong>in</strong>es Galgens. Man gehe vom Galgen auf geradem<br />
Wege zum Baum A und zähle dabei die Schritte. Bei A wende man sich um neunzig Grad<br />
nach l<strong>in</strong>ks, gehe nochmals die gleiche Schrittzahl geradeaus und markiere die erreichte Stelle<br />
mit e<strong>in</strong>em Stock. Dann begebe man sich zurück zum Galgen, gehe auf geradem Weg zum<br />
Baum B, zähle wie<strong>der</strong> die Schritte, wende sich bei B um neunzig Grad nach rechts und gehe<br />
die gleiche Schrittzahl geradeaus. Die erreichte Stelle werde wie<strong>der</strong> mit e<strong>in</strong>em Stock markiert.<br />
Wenn man dann genau <strong>in</strong> <strong>der</strong> Mitte zwischen den beiden Stöcken gräbt, so wird man auf den<br />
Schatz stossen.<br />
E<strong>in</strong> junger Abenteurer, <strong>der</strong> die Urkunde fand, mietete sich e<strong>in</strong> Schiff und segelte zur Insel. Er<br />
hatte ke<strong>in</strong>e Mühe, die Bäume zu f<strong>in</strong>den, aber zu se<strong>in</strong>em Jammer war <strong>der</strong> Galgen<br />
verschwunden, und die Zeit hatte alle Spuren verwischt, so dass die Stelle , an <strong>der</strong> sich <strong>der</strong><br />
Galgen befunden hatte, nicht mehr zu erkennen war. Der junge Mann war ratlos und kehrte<br />
mit leeren Händen zurück. Nach Gamow hätte er den Schatz mit Leichtigkeit f<strong>in</strong>den können.<br />
AG 90° im Uhrzeigers<strong>in</strong>n um A drehen<br />
z = z − i ⋅ z − z<br />
A'<br />
A<br />
( )<br />
G<br />
komplex_4_k 20.08.2012 20:49:00<br />
A<br />
BG 90° im Gegenuhrzeigers<strong>in</strong>n um B drehen<br />
z = z + i ⋅ z − z<br />
B ( G B )<br />
1<br />
1<br />
2 ( zA'<br />
+ zB<br />
' ) = 2 ( z A + zB<br />
+ i(<br />
zA<br />
− z ) )<br />
( 1+<br />
( −1)<br />
− 2i)<br />
= −i<br />
B'<br />
zS =<br />
B<br />
=<br />
1<br />
2<br />
Lösung:<br />
Drehe A um 90° im Gegenuhrzeigers<strong>in</strong>n<br />
um die Mitte M von AB.<br />
11