Trigonometrische Gleichungen

11. Trigonometrische Gleichungen
Typ „Ausklammern“
sin(2x) - cos x = 0 Wende die Additionstheoreme und Grundbeziehungen an
2 sin x cos x - cos x = 0 Ausklammern
cos x (2 sin x - 1) = 0
cos x = 0 90°, 270°
sin x = 0.5 30°, 150°
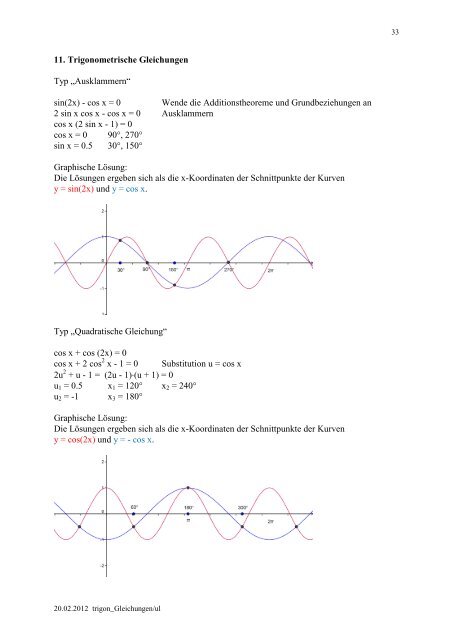
Graphische Lösung:
Die Lösungen ergeben sich als die x-Koordinaten der Schnittpunkte der Kurven
y = sin(2x) und y = cos x.
Typ „Quadratische Gleichung“
cos x + cos (2x) = 0
cos x + 2 cos 2 x - 1 = 0 Substitution u = cos x
2u 2 + u - 1 = (2u - 1) (u + 1) = 0
u1 = 0.5 x1 = 120° x2 = 240°
u2 = -1 x3 = 180°
Graphische Lösung:
Die Lösungen ergeben sich als die x-Koordinaten der Schnittpunkte der Kurven
y = cos(2x) und y = - cos x.
20.02.2012 trigon_Gleichungen/ul
33

Typ: a sin x + b cos x + c = 0
Spezialfall c = 0
a sin x + b cos x = 0 Dividiere durch cos x 0 (cos x = 0 liefert keine Lösungen!)
Die Lösungen ergeben sich aus der Gleichung tan x = - b/a.
B.
sin x = 2 cos x tan x = 2 x1 = 63.2°, x2 = x1 + 180° = 243.2°
allg. Fall:
prüfe, ob x = 180° eine Lösung der Gleichung ist.
Mit den sogenannten Rationalisierungformeln kann die Gleichung in eine quadratische
Gleichung übergeführt werden:
2
2t 1 t
2
2
x
a b c 0 2at
b ( 1 t ) c ( 1 t ) 0 wobei t tan 2
2
1 t 1 t
2
B:
3sin x - 2cos x + 3 = 0 5t 2 + 6t + 1 = 0
t1 = - 0.2, t2 = -1 x1 = 337.5°, x2 = 270°
Grafische Lösung:
In der Abbildung ergeben sich die Lösungen
als Nullstellen der Funktion
f ( x) 3sin x 2cos x 3
Uebungsaufgabe:
2cos x - sin x + 2 = 0 t 2 + t - 2 = 0
Lösungen: x1 = 90°, x2 = 240°
20.02.2012 trigon_Gleichungen/ul
34

Viele trigonometrische Gleichungen sind nur durch Näherungsverfahren lösbar
Der Bisektionsalgorithmus (Intervallhalbierung)
Es handelt sich um ein Verfahren zur Bestimmung der Nullstellen einer Gleichung f(x) = 0.
Vor.
f stetig in [a,b] und f(a) < 0 und f(b) > 0 d.h. f hat an den Intervallgrenzen verschiedene
Vorzeichen (gegebenenfalls kann die Gleichung mit (-1) multipliziert werden).
Nach dem Zwischenwertsatz hat dann f mindestens eine Nullstelle im Innern des Intervalls
d.h. der Graph von f schneidet mindestens einmal die x-Achse.
Die Lösung wird nun schrittweise durch Halbieren des Intervalls angenähert.
Bisektionsalgorithmus (nach Gander):
x := (a + b)/2 bestimme die Intervallmitte
while (b - a) > do tue solange die gewünschte Genauigkeit nicht
begin erreicht ist (*)
if f(x) > 0 then b := a else a := x Wahl des nächsten Intervalls
x := (a + b)/2 neue Intervallmitte
end
(*) Verbesserte Abbruchbedingung: while (a < x) and (x < b)
Illustration am Beispiel cos x = x f x cos x x
Die Voraussetzung ist im Intervall [0,1] erfüllt.
Die Gleichung hat die Lösung x = 0.73908513…
20.02.2012 trigon_Gleichungen/ul
35

Lösung mit Iterationsverfahren bei Gleichungen der Form g(x) = x
Iteration:
Rechenvorgang, der sich ständig wiederholt, wobei die gesuchte Lösung schrittweise besser
angenähert wird.
Illustration des Verfahrens am gleichen Beispiel cos x = x:
In der Abbildung sind die Kurven y = cos x und y
= x dargestellt.
Wähle einen Startwert x1 = 0.5 und berechne
schrittweise xk+1 = cos xk.
Es entsteht in der Abbildung ein spiralförmiger
Streckenzug der sich dem Grenzpunkt
mit x = 0.739085133.. immer mehr nähert.
Bem.:
Es kann gezeigt werden, dass dieses Verfahren konvergiert, wenn der Graph der Funktion
nicht steiler als die Winkelhalbierenden steigt bzw. fällt. ( Numerische Verfahren).
20.02.2012 trigon_Gleichungen/ul
36

12. Eine Aufgabe aus der Astronomie
Anwendung aus der Astronomie:
Berlin und Kapstadt liegen nahezu auf demselben Längenkreis (Meridian). Die Astronomen
Lalande in Berlin und Lacaille in Kapstadt haben 1751 zur gleichen Zeit die folgenden
Zenitdistanzen desselben Mondrandes gemessen:
Berlin 1 = 52 31'13'' Zenitdistanz z1 = 41 15'44''
Kapstadt 2 = -33 55'15'' Zenitdistanz z2 = 46 33'37''
Berechne daraus die Entfernung Erde - Mond (Erdradius R = 6371.2 km)
Führe die Hilfswinkel 1 und 2 ein
Sinussatz im Dreieck OMB:
R
sin 1
d
sin( 180 z1)
d
sin z1
Sinussatz im Dreieck OKB:
R
sin
d
sin( 180 z )
d
sin z
Winkelsumme im Viereck 1 + 2 = z1 + z2 - 1 - 2 = a
2 = a - 1 (3)
aus (1) und (2):
d
R
sin z1
sin 1
sin z2
sin 2
(4)
aus (4)
sin
sin
2 sin z2
sin z
b
(5)
Additionstheorem und (5‘)
20.02.2012 trigon_Gleichungen/ul
2
1
1
2
2
(1)
(2)
sin 2 b sin 1
(5’)
sin sin( a )
sina
2
cos
1
1
cosa
dividiere durch cos 1 sina cosa
tan 1 b tan 1
tan 1 ausklammern sina tan 1 (cosa
b)
b
tan 1
sin a
b cosa
1 arctan
sin a
b cosa
sin
1
b
sin
1
(6)
37

Numerische Resultate:
aus (5) b = 1.100972471
aus (3) a = 1.381388888
aus (6) 1 = 0.657498153
aus (3) 2 = 0.723890734
aus (4)
d R
sin z1
= 57.4720247 R = 366165 km
sin
20.02.2012 trigon_Gleichungen/ul
1
38