10. Klasse - Finsterwalder Gymnasium

M 10.1
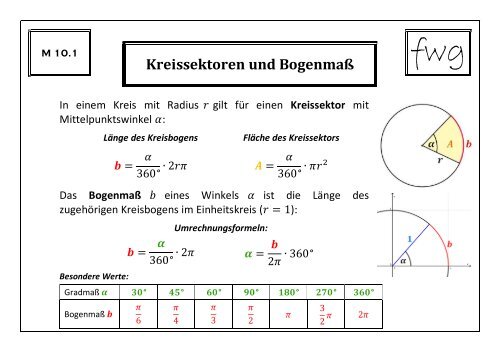
Kreissektoren und Bogenmaß
fwg
In einem Kreis mit Radius
Mittelpunktswinkel :
Länge des Kreisbogens
gilt für einen Kreissektor mit
Fläche des Kreissektors
Das Bogenmaß eines Winkels ist die Länge des
zugehörigen Kreisbogens im Einheitskreis ( ):
Umrechnungsformeln:
Besondere Werte:
Gradmaß
Bogenmaß

M 10.2
Kugel
fwg
Ist
der Radius einer Kugel, so gilt:
‣ Volumen:
‣ Oberfläche:

M 10.3
Sinus und Kosinus
für beliebige Winkel
fwg
Für beliebige Winkel
gibt
‣ der Sinus die -Koordinate:
‣ der Kosinus die -Koordinate:
eines Punktes an, der unter auf dem Einheitskreis liegt.
Die Sinuswerte (bzw. Kosinuswerte ) haben für den spitzen Winkel
sowie für die Winkel und
denselben Betrag. Die Vorzeichen liefern die Quadranten:
Alle anderen Winkel lassen sich durch Addition und Subtraktion von
Vielfachen von auf einen Winkel zwischen und zurückführen.
am Einheitskreis
am Einheitskreis

M 10.4
Sinus- & Kosinusfunktion
fwg
im Gradmaß
im Bogenmaß
Eigenschaften:
Sinusfunktion
periodisch mit der Periode
Kosinusfunktion
periodisch mit der Periode
Definitionsmenge
Wertemenge
punktsymmetrisch zum Ursprung
achsensymmetrisch zur -Achse

M 10.5
Die allgemeine Sinusfunktion
fwg
Durch die allgemeine Sinusfunktion
beliebige sinusförmige Graphen beschreiben:
lassen sich
‣ : Stauchung/Streckung in -Richtung
(Amplitude)
‣ b: Stauchung/Streckung in -Richtung.
‣ c: Verschiebung in -Richtung
‣ d: Verschiebung in -Richtung
‣ : Doppelter Ausschlag nach oben ( )
‣ : Doppelte Periode ( )
‣ : Verschiebung um nach links
‣ : Verschiebung um nach unten

M 10.6
Lineares und exponentielles
Wachstum
fwg
Lineares Wachstum
Konstanter Zuwachs pro Zeiteinheit
Exponentielles Wachstum
Konstanter Wachstumsfaktor in gleichen
(Zeit-) Schritten
Nimmt die Größe um zu, so wächst die
Größe stets um einen festen Summanden .
Nimmt die Größe um zu, so wächst die
Größe stets um einen festen Faktor .

M 10.7
Exponentialfunktion
fwg
Funktionen der Form ( , , , ) heißen
Exponentialfunktionen. Die Konstante gibt den Wachstumsfaktor an. Die
Konstante gibt den Anfangswert der Funktion für an, also ist .
Für
steigt der Graph
Wachstum
Für fällt der Graph
negatives Wachstum
Der Graph verläuft durch den
Punkt .
Die -Achse ist Asymptote.
Spiegelt man den Graphen von
so erhält man den Graphen von
Ist , so wird der Graph
in -Richtung mit dem
Faktor gestreckt )
bzw. gestaucht (|b| ).
Ist , so wird der
gestreckte/gestauchte Graph
zusätzlich an der -Achse
gespiegelt.
an der -Achse,
und umgekehrt.

M 10.8
Logarithmus
fwg
Die eindeutige Lösung der (Exponential-)Gleichung (für , ,
) bezeichnet man als Logarithmus von zur Basis und schreibt
:
„Logarithmus“ ist ein Name für „Exponent zu einer bestimmten Basis“:
Rechenregeln:
‣ (Produktregel)
‣ (Quotientenregel)
‣ (Potenzregel)
‣ (Wechsel der Basis)

M 10.9
Exponentialgleichungen
fwg
Bei einer Exponentialgleichung tritt die Unbekannte im Exponenten auf.
Es gibt verschiedene Arten von Exponentialgleichungen, für die es
unterschiedliche Lösungsstrategien gibt:
Logarithmieren Substitution Grafisch
Exponentialgleichungen, die
in die Form gebracht
werden können, löst man
durch Logarithmieren:
Substitution: (
Lösung der quadratischen
Gleichung und Resubstitution
liefert das Ergebnis:
Exponentialgleichungen in denen die
Unbekannte im Exponenten und in
der Basis auftreten sind rechnerisch
unlösbar.
Eine näherungsweise
Lösung bietet das
Zeichnen in einem
Koordinatensystem:

M 10.10
Ereignisse und Vierfeldertafel
fwg
Ereignisse sind Teilmengen der Ergebnismenge, beim einfachen Würfelwurf mit
z.B. „Augenzahl gerade“ A = {2, 4, 6} bzw. „Augenzahl prim“ B ={2, 3, 5}.
Mit den Ereignisverknüpfungen erhält man:
„Komplement von A“: „A und B“: „A oder B“:
ist
Statistische Angaben über zwei Merkmale mit jeweils zwei Merkmalsausprägungen stellt man
üblicherweise in einer sog. Vierfeldertafel dar. Diese kann Anzahlen oder auch Wahrscheinlichkeiten
enthalten. Die Wahrscheinlichkeiten findet man auch im zugehörigen Baumdiagramm.
1. Merkmal
( )
2. Merkmal
( )

M 10.11
Bedingte Wahrscheinlichkeit
fwg
ist die Wahrscheinlichkeit von unter der Bedingung, dass
eingetreten ist. Die möglichen Ergebnisse sind nur noch die Ergebnisse von .
Die günstigen Ergebnisse sind die Ergebnisse von , bei denen zusätzlich
eintritt (“Anteil vom Anteil des Ganzen”).
1. Baumdiagramm 2. Baumdiagramm
1. Merkmal ( ) 2. Merkmal ( ) 1. Merkmal ( ) 2. Merkmal ( )
Berechnung:

M 10.12
Bedingte Wahrscheinlichkeit
Beispiel Baumdiagramm – 4-Feldertafel
fwg
In einem Betrieb kommt es an 1% aller Arbeitstage zu einem Brand. In 90%
dieser Fälle wird ein automatischer Alarm ausgelöst. Liegt kein Brand vor, so
gibt es mit einer Wahrscheinlichkeit von 5% einen Fehlalarm. Berechne, wie
groß ist die Wahrscheinlichkeit dafür ist, dass es wirklich brennt, wenn ein
Alarm ausgelöst wird?
A:= „Alarm wird ausgelöst“
Geg.:
B:= „Es brennt im Betrieb“

M 10.13
Ganzrationale Funktionen
fwg
Grad
Potenzfunktionen
Koeffizienten
Polynom
ganzrationale Funktion
Beispiel für qualitativen Verlauf des Graphen einer ganzrationalen Funktion:
höchster vorkommende Exponent
(hier )
gerade
ungerade
Leitkoeffizient
(hier )
„von links oben nach
rechts oben“
„von links unten nach
rechts unten“
„von links unten nach
rechts oben“
„von links oben
nach rechts unten“

M 10.14
Nullstellen einer ganzrationalen
Funktion
fwg
Eine ganzrationale Funktion -ten Grades hat höchstens Nullstellen.
Beispiel zur Bestimmung der Nullstelle(n) der Funktion
Errate Nullstelle durch
systematisches
Probieren
(NST Teiler von )
Schreibe Funktion als
Produkt mit Restpolynom
Polynomdivision
Restliche Nullstellen
durch Mitternachtsformel
(bzw. Vieta) bestimmen
falls Grad des Restpolynoms
Faktorisierte Form: (doppelte Nullstelle bei )
Tritt in der vollständig faktorisierten Form eine Nullstelle
‣ ungeradzahlig oft auf, wechselt bei das Vorzeichen,
‣ geradzahlig oft auf, wechselt bei das Vorzeichen nicht.

M 10.15
Polynomdivision
fwg
Beispiel:

M 10.16
Verschieben, Strecken/Stauchen/
Spiegeln von Funktionsgraphen
fwg
(vgl. M10.5)
Verschiebung von Funktionsgraphen
‣ Verschiebung um in -Richtung (Ausklammern von b)
‣ Verschiebung um d in -Richtung
Strecken (Stauchen) von Funktionsgraphen
‣ Stauchung/Streckung um in -Richtung.
‣ Stauchung/Streckung um a in -Richtung
Spiegelung an der -Achse / -Achse /
am Ursprung
‣ liefert den an der -Achse gespiegelten Graph von
‣ liefert den an der -Achse gespiegelten Graph von
‣ liefert den am Ursprung gespiegelten Graph von

M 10.17
Symmetrie von Funktionsgraphen
fwg
Achsensymmetrie zur -Achse
Punktsymmetrie zum Ursprung
Gleich weit vom Nullpunkt entferte -Werte
besitzen stets denselben Funktionswert.
Gleich weit vom Nullpunkt entfernte -
Werte besitzen stets den betragmäßig
gleichen Funktionswert mit
unterschiedlichem Vorzeichen.
Ganzrationale Funktionen sind achsensymmetrisch, wenn sie nur geradzahlige Exponenten
besitzen und punktsymmetrisch, wenn sie nur ungeradzahlige Exponenten besitzen.

M 10.18
Verhalten im Unendlichen
fwg
Konvergenz
Kommen die Funktionswerte einer
Funktion für beliebig groß werdende -
Werte einer Zahl beliebig nahe, so
nennt man den Grenzwert der Funktion
für gegen unendlich ( ).
Die Gerade mit der Gleichung ist
dann waagrechte Asymptote von
Divergenz
Wachsen die Funktionswerte für
bzw. unbegrenzt nach
oder sinken sie unbegrenzt nach , so
divergiert die Funktion (bestimmte Divergenz)
d.h. sie besitzt keinen Grenzwert .
kein Grenzwert
unbestimmt
divergent

M 10.19
Strategien zum Untersuchen des
Verhaltens im Unendlichen
fwg
Ganzrationale Funktionen
und
vgl. 10.13
Gebrochen rationale Funktionen
Ausklammern und Kürzen der höchsten Nennerpotenz:
größte Nennerpotenz
geht gegen
=
Exponentialfunktionen
+
-
geht gegen
also besitzt Graph waagrechte
Asymptote y = 3 mit Annäherung
von unten für x .
vgl. 10.7

M 10.20
Grundfunktionen
fwg
Name Term Beispiel Graph
1
2
3
4
5
6
Lineare
Funktionen
Quadratische
Funktionen
Ganzrationale
Funktionen
Gebrochen
rationale
Funktionen
Exponentialfunktionen
Winkelfunktionen