x - Gmehling

11.02.99
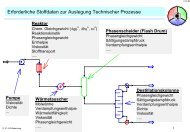
Schema einer Vinylacetat-Anlage (vereinfacht)
C 2 H 4 + CH 3 COOH + ½ O 2
CH 3 COOCH=CH 2 + H 2 O
(exotherm)
101 01 016 Bedeutung
Nebenreaktionen, z.B.:
C 2 H 4 + 3 O 2 2 CO 2 + 2 H 2 O
(Acetaldehyd, Ethylacetat, .. )
1

Stoff- und Wärmetransportmechanismen
Stofftransport
Wärmetransport
molekulare Ebene molekulare Diffusion Wärmeleitung
makroskopische Ebene
(„effektiver Transport“)
Konvektion
(zu unterscheiden:
freie und erzwungene
Konvektion)
konvektiver
Wärmetransport
(an konvektivenStofftransport
gebunden)
Wärmestrahlung
(insbesondere bei
hoher Temperatur)
2

Filmtheorie
P Gas
Grenzfläche
(Interface)
Phase''
(z.B. reines Gas)
oder Gipskristall,
Kandis, ..
∆z'
c '
i
Phase'
Prandtl‘sche Grenzschicht
c'
z
nɺ
β
nɺ
iL
= β A c
L
β ≈ D
∆ z
( ' − c ' )
Molenstrom [kmol/h]
Stoffübergangskoeffizient
[m/h]
A Phasengrenzfläche [m 2 ]
c Konzentration [kmol/m 3 ]
i
3

Polarographie (1921 Heyrovsky, Chemie-Nobelpreis 1959)
4

CO 2 -Abtrennung durch Pottaschewäsche in der Vinylacetatanlage
K 2
CO 3
C 2
H 4
nɺ
iL
= β
L
( ' ) − c '
A c
i
CO 2
, C 2
H 4
KHCO 3
-Lösung
Optimaler Stofftransport
bei großen
Stofftransportkoeffizienten
(d.h. turbulenten
Bedingungen), großen
Oberflächen (d.h. kleinen
Gasblasen) und großen
Konzentrationsdifferenzen
Kein reines Gas; auch Stofftransportwiderstand auf der Gasseite,
Filmtheorie Zweifilmtheorie
5

Filmtheorie
(Stoffübergang G L)
c''
(
''
c
i' ' )
nɺ
= β A c −
G
iG
nɺ
iL
= β
L
( − c
' )
A c
Im stationären
Zustand:
'
i
Phase''
Annahme:
Phasengleichgewicht
c '' i
Grenzfläche
∆z''
∆z'
c ' i
c
Phase'
= H c
'' '
c '' = K .
i c iji'
i
c'
z
nɺ
iL
=
nɺ
iG
H ij
c''
c
Phase''
'*
'' = H
c'' = K . c ijc
'* i
Henry-Koeffizient,
Verteilungskoeffizient
K = Henry-Koeffizient,
Verteilungskoeffizient....
i
c '* i
Phase'
∆z'
c'
z
6

Stofftransport Zweifilmtheorie
c '' − c =
c
'
i
''
i
'
− =
c
nɺ
iG
βGA
nɺ
iL
β A
L
(1)
c''
Gas
c'' i
c' i
c' i
*
Flüssigkeit
c'
DurchAdditionvonGl.1und2
L G
( nɺ = nɺ = nɺ
)
i i i
⎛
'* ' 1 1 ⎞ nɺ
i
ci
− c = +
⎜
Hij βG β ⎟
⎝
L ⎠ A
Konzentrationen an der
Phasengrenzfläche :
Nach Einführung des Stoffdurchgangskoeffizienten
k [ m/h ]:
c H c c H c
'* '' '
'' =
ij i i
=
ij i
Durch Substitution erhält man:
n
H c − c = ɺ
( )
'* ' iG
ij i i
βG
(
'* '
c ) i
ci
− =
nɺ
G
iG
β H A
ij
A
(2)
1 1 1
= +
kL HijβG βL
erhält man für den Stoffdurchgang:
i
L
(
'* '
)
nɺ
= k A c − c
7

Messmethoden zur Bestimmung von A, k L und k L A
Best_A_kl_a.cdr
Grenzfläche A:
n = k A c
i L,i
∆ i
G
Fotografie
L
Sonde
G
L
isokinetische
Absaugung
Stoffdurchgangskoeffizient k L
G, P CO2 G
k A L
definierte
Fläche
c 0,N2 H 4 Luft
L L, c CO2 Hydrazinmethode
Luft c N2 H 4
(für wässrige Systeme)
8

CO 2 -Abtrennung durch Pottaschewäsche in der Vinylacetatanlage
K 2
CO 3
C 2
H 4
a) Änderungen der Konzentration
b) Änderung des Druckes und damit
der Oberfläche als f(Höhe)
c) Koaleszenz
d) Einfluss der chemischen Reaktion
auf den Stofftransport
CO 2
, C 2
H 4
KHCO 3
-Lösung
9

Beschleunigung des Stofftransports durch chemische Reaktion
Beschleunigung wird
durch Enhancement-
Faktor beschrieben!
A(1) + B(2) C
a e: langsame Reaktion momentane Reaktion an der Phasengrenzfläche
10

11.02.99
Schema einer Vinylacetat-Anlage (vereinfacht)
Durchmesser der Rohre
abhängig von Kinetik,
Reaktionsenthalpie und
Effektivität des
Wärmetransports (Kühlung)
C 2 H 4 + CH 3 COOH + ½ O 2
CH 3 COOCH=CH 2 + H 2 O
(exotherm)
Wie sehen die
Wärmetauscher aus?
101 01 016 Bedeutung
Nebenreaktionen, z.B.:
C 2 H 4 + 3 O 2 2 CO 2 + 2 H 2 O
(Acetaldehyd, Ethylacetat, .. )
12

Stoff- und Wärmetransportmechanismen
Stofftransport
Wärmetransport
molekulare Ebene molekulare Diffusion Wärmeleitung
makroskopische Ebene
(„effektiver Transport“)
Konvektion
(zu unterscheiden:
freie und erzwungene
Konvektion)
konvektiver
Wärmetransport
(an konvektivenStofftransport
gebunden)
Wärmestrahlung
(insbesondere bei
hoher Temperatur)
13

Wärmeleitung
einfachster Fall: ebene Wand z.B. Stahl [stationärer Zustand]
T 0
T 1
1. Fouriersche Gleichung
Q ɺ
z
λ - Wärmeleitzahl [W/mK]
z - Wanddicke [m]
A - Fläche [m 2 ]
Q ɺ - Wärmestrom [W]
- Wärmestromdichte [W/m 2 ]
qɺ
Qɺ
= − λ A
dT
dz
Für den Wärmestrom Q ɺ [W] gilt:
Qɺ
λ
λ
= A ( T − T ) = A ∆
z
z
Wärmestromdichte:
0 1
T
Qɺ
qɺ
λ
λ
= = ( T − T ) = ∆
A z z
0 1
T
14

Wärmeleitung durch eine mehrschichtige Wand
Im stationären Fall gilt:
15

Wärmeleitzahlen λ [ W/mK] für ausgewählte Stoffe bei 20°C*
* Nach dem Wiedemann-Franzschen Gesetz besitzen elektrisch gut
leitende Stoffe auch einen geringen Widerstand bei der Wärmeleitung
Schlechteste Wärmeleiter sind Gase. Darauf beruht Einsatz poröser
Isoliermaterialen.
16

Wärmeleitfähigkeit
verschiedenster
fester, flüssiger und
gasförmiger
Verbindungen in
Abhängigkeit von der
Verbindungen
( VDI-Wärmeatlas
1985, 5. Auflage )
17

Beispiel: Wärmeleitzahl λ von Toluol (flüssig) bei 25°C
Messung der Wärmeleitzahl von
Flüssigkeiten und Gasen nicht
einfach (Konvektion muss
vermieden werden !!).
18

Wärmestrahlung
Bilanz für eingestrahlte Energie
• • • •
Q = Q + Q + Q
r
a
d
r a d
reflektiert
absorbiert
durchgelassen
Grenzfälle
idealer Spiegel:
schwarzer Körper:
diathermer Körper:
• •
Q r
• •
= Q a
• •
= Q d
Q =
Q
Q
Ausgestrahlte Energie eines schwarzen Körpers
nach Stefan-Bolzmann:
•
4
Qs
= Cs
A T W
C s
Strahlungszahl des schwarzen Körpers
(5.676 . 10 -8 W/m 2 K 4 )
Wiensches Verschiebungsgesetz:
−
λ max T = 2.
885⋅10 3 mK
19

Wärmestrahlung
λ
T
T
Temperatur Sonne:
max
T
= 2.885⋅10
2.885⋅10
=
500⋅10
= 5770K
−3
−9
−3
mK
m
mK
500 nm
Verteilung der relativen Strahlungsenergie E λ
des schwarzen Körpers auf die Wellenlänge λ bei
verschiedenen Temperaturen T nach M. Planck
sichtbares Spektralgebiet schraffiert
20

Strahlung des
schwarzen
Körpers
21

In der Realität gibt es keine schwarzen Körper
GrauerKörper:
ɺ
4
Q=CsεAT [W]
ε Emissionsverhältnis
Pt-Schwarz, Lampenruß ε = 0.9 – 0.97
Ziegel ε = 0.9
Schamott (Steamcracker) ε = 0.6
Stahl ε = 0.6
Polierte Oberflächen ε = 0.04
Kupfer poliert ε = 0.03
durch Keramik-
Coating ε = 0.9
22

Konvektiver Stofftransport (freie bzw. erzwungene Konvektion)
Konvektiver Stofftransport: Wichtigster Stofftransport in der Praxis (Heizen,
Wärmetauscher)
Zu unterscheiden:
Wärmeübergang
Wärmedurchgang
Konvektiver Wärmetransport an Stofftransport gebunden
Qɺ
= α ⋅ A ⋅ ∆T
α
Wärmeübergangskoeffizient W/m2 K (Wert hängt von
Strömungseigenschaften, Oberflächenbeschaffenheit, Dicke der
Prandtlschen Grenzschicht, ... ab)
23

Beispiele für Wärmeübergangszahlen α [ W/m 2 K]*
α [ W/m 2 K] niedrig mittel hoch
Luft 8 40 80
Wasser 100 1000 4000
siedendes Wasser 1000 6000 30000
kondensierendes
Wasser
kondensierende
organische Dämpfe
5000 14000 25000
500 1000 2000
zu berechnen über dimensionslose Kennzahlen:*
Nusselt - Zahl Nu = tatsächlicher Wärmestrom
Wärmestrom durch Wärmeleitung
Nu = f(Re,Pr) z.B.: Nu = C Re n Pr m
αz
=
λ
* VDI-Wärmeatlas
24

Wärmestromdichte als f(∆T) für Wasser bei 1 bar
H. Martin, Kap. 3.2
in Fluid-Verfahrenstechnik,
Band 1, S. 281
Herausgeber:
R. Goedecke
Wiley-VCH, Weinheim (2006)
25

Nukijama-Kurve
Nukijama-Kurve, A freie Konvektion, B Blasenverdampfung,
C instabile Filmverdampfung, D stabile Filmverdampfung
Nukijama, S.: The maximum and minimum values of the heat Q transmitted from
metal to boiling water under atmospheric pressure. J. Jap. Soc. Mech. Eng. 37 (1934)
367-374, engl. Übersetzung in Int. Heat Mass Transfer 9 (1966) 1419-1433
26

Wärmedurchgang (z.B. Wärmetauscher, Rohrbündelreaktor, .. )
Wärme
T
T
1
T
W,1
∆z
T
W,2
z
T
2
27

Wärmedurchgang
•
Q
= T1
Aα1
•
Q ∆z
Aλ
−
T W ,1
= T W
−T
, 1 W ,2
T
T
1
T
Wärme
W,1
bzw. unter Verwendung
der Wärmedurchgangszahl k:
•
Q
=
k A ∆T
•
Q
Aα
2
=
T
W ,2
−T
2
∆z
T
W,2
z
T
2
wobei für k gilt:
•
Q
A
⎛ 1
⎜
⎝α1
+
∆z
1
+
λ α
2
⎞
⎟
⎠
=
T
1
−T
2
1
k
=
1
α
1
+
∆z
1
+
λ α
2
28

∆T bei Gleichstrom
29

∆T bei Gegenstrom
30

∆T beim Wärmetauscher
Durch eine Wärmebilanz lässt sich zeigen, dass ∆T durch
logarithmische Temperaturdifferenz ersetzt werden muss:
∆ T
=
ln
∆
T
A
ln
− ∆
T
∆TA
∆T
E
E
Damit ergibt sich die folgende Beziehung für den
Wärmedurchgang beim Wärmetauscher:
Qɺ
= k A ∆
T ln
31

Einfluss der Stromführung auf die Fläche eines Wärmeaustauschers
1000 kg/h Öl (c p
=0,45 kcal/kg K) sollen mit
Wasser (c p
=1,0 kcal/kg K) von 100°C auf 50°C
abgekühlt werden. Das Wasser soll von 20°C
auf max. 40°C erwärmt werden. Welche Menge
an Wasser wird benötigt und wie groß ist die
Austauschfläche bei Gleich- und bei Gegenstromführung?
(k=200 kcal/m 2 h K)
32

Temperaturprofile bei der Kühlung und Kondensation überhitzter Dämpfe
Bei Unstetigkeiten im
Temperaturverlauf z.B.
der Kondensation von
Dämpfen:
Berechnung der
Gesamtfläche aus den
einzelnen Teilflächen
A ges = A 1 + A 2
33

Umlaufverdampfer (natürlicher Umlauf) einer Rektifikationskolonne
34

Wärmeaustauscher (Rohrbündelreaktor)
35

Think Big (LURGI)
36

Temperaturverlauf Rohrreaktor bei exothermer Reaktion
Temperatur
ɺ ɺ ɺ ɺ
Q R
> Q A
A B
Thot spot = f (r,V,c Ao
,∆h R
,k W
,k(T)) z.B. . −r Α = k(T) c A
Q R < Q A
ɺ
dQA kW dA ∆T= kW
2 π
Reaktionsmedium ɺ
dQ R
= k(T)
⋅cA ⋅dVR ⋅( −∆h
R)
2
steigende k(T)
= k(T) ⋅cA
⋅ π⋅r ⋅dL ⋅( −∆h
R )
sinkende Konz. c A
∆T L2
= ⋅ ⋅ ⋅ ⋅ ⋅r ⋅dL
⋅∆T
Temperatur T
∆T L1
T Kühlmittel
(z.B. siedendes Wasser bei entsprechendem Druck)
Länge L
37

Zusammenfassung Wärmetransport
1) Wärmeleitung
T
Qɺ
∂
= −λ
⋅ A ⋅
∂z
λ = Wärmeleitzahl
[ W/mK ]
2) Wärmestrahlung
Qɺ
=
C
s
⋅ A
⋅ T
4
(schwarzer
Körper)
Qɺ
= ε ⋅C
s
⋅ A
⋅T
4
(grauer
Körper)
3) Konvektion
Wärmeübergang
Qɺ
= α ⋅A
⋅∆T
α
α
α
= Wärmeübergangszahl [ W/m
2
K]
= f(Geometrie,Strömungseigenschaften,...)
= f(Nu,Pr ,Re,...)
38

Zusammenfassung: Wärmedurchgang, Wärmeaustauscher
•
Q
=
k
⋅
A
⋅ ∆T
k = Wärmedurchgangszahl (W/m 2 K)
z. B. ebene Wand
1
k
1 zi
1
= + ∑ +
α λ α
I
i
II
I
II
Wärmeaustauscher:
Möglichkeiten der Stromführung
a) Gleichstrom
b) Gegenstrom
∆T
ln
∆T
ln
=
=
∆Tgroß
− ∆T
∆Tgroß
ln
∆T
klein
klein
logarithmische Temperaturdifferenz
c) Kreuzstrom
•
Q = k ⋅ A
⋅
∆
T ln
39

Inhalt der Vorlesung „Grundlagen der Technischen Chemie“
Unterschied Labor - Technik
a) größerer Maßstab b) Wirtschaftlichkeit
Geschichte der industriellen Chemie
Rohstoff und Energiesituation
Grundfließbild, Verfahrensfließbild
Grundbegriffe (Umsatz, Selektivität,
Ausbeute)
Produkte der chemischen Industrie
Grundlagen
Thermische Trennverfahren
Rektifikation, Extraktion, Absorption, Kristallisation,
Adsorption, Membrantrennverfahren
Aufstellung und Lösung von Bilanzgleichungen
a) Reaktionstechnik (CSTR, PFR)
b) Grundoperationen (z.B. Rektifikation)
Herstellung der Grundchemikalien
Erdöldestillation, Chemische Raffinerie
Steamcracker (C4- und Aromatenaufarbeitung)
Steamreforming
Produktstammbäume
Reaktionskinetik (homogen)
Stofftransport
Wärmetransport
Thermodynamik
a) Reaktionsenthalpie, chemisches
Gleichgewicht
b) Phasengleichgewicht
c) Stoffdaten
Ausgewählte Chemische Prozesse
Vinylchlorid
Ethylenoxid
Kostenrechnung
40

Einsatzmöglichkeiten der Thermodynamik
im Chemieingenieurwesen
• Berechnung der Reaktionsenthalpie (∆h R (T,P))
• Berechnung des Gleichgewichtsumsatzes als f(T,P,x i )
für einfache reversible Reaktionen und Simultangleichgewichte
• Berechnung der verschiedenen Phasengleichgewichte
(VLE, LLE, ..) zur Auslegung thermischer
Trennverfahren
• Berechnung weiterer wichtiger Daten (Enthalpien,
Dichten, Wärmekapazitäten, ... ∆h R (P))
• Auslegung von Kreisprozessen
41

Reaktionsenthalpie, Standardreaktionsenthalpie
Reaktionsenthalpie ist identisch mit der Differenz der
Enthalpieinhalte von Produkten und Edukten
∆h R (T,P) = Σ ν i h i (T,P)
Tabellierung aller ∆h R (T,P) nicht möglich!
Festlegung eines Standardzustandes (25 °C, 1 atm) (Flüssigkeit,
Feststoff, fiktives ideales Gas)
auch dann verbleibt große Anzahl möglicher
Standardreaktionsenthalpien
42

Berechnung der Standardreaktionsenthalpie
aus den Standardbildungsenthalpien
Die Standardbildungsenthalpie ist gleich der
Standardreaktionsenthalpie aus den Elementen.
Einige experimentell zugänglich, z.B.:
C + O 2 → CO 2 ∆h R
o
H 2 + ½ O 2 → H 2 O ∆h R
o
H 2 → H 2 ∆h Ro = 0
Standardbildungsenthalpien der Elemente = 0. Andere Werte über
andere Reaktionsenthalpien, z.B. Verbrennungsenthalpien, ..
zugänglich:
C 6 H 6 + 7.5 O 2 → 6 CO 2 + 3 H 2 0 ∆h Verbrennung
43

Berechnung der Standardreaktionsenthalpie aus den
Standardbildungsenthalpien
CH 3 OH → C + 2 H 2 + ½ O 2 -∆h o B,CH3OH
CO → C + ½ O 2 -∆h o B,CO
2 C + 2 H 2 + O 2 → CH 3 COOH ∆h o B,CH3COOH
CH 3 OH + CO → CH 3 COOH ∆h R
o
∆h Ro = ∆h o B,CH3COOH -∆h o B,CH3OH -∆h o B,CO = Σν i ∆h o B,i
Temperaturabhängigkeit der Standardreaktionsenthalpie
(Kirchhoffsches Gesetz):
∆h Ro (T) = ∆h Ro (T o ) + Σ ν i c Pio dT
44

Druckabhängigkeit der Reaktionsenthalpie
0.5 N
2
+ 1.5 H
2
⇌ NH3
Druckabhängigkeit mit
Hilfe von
Zustandsgleichungen
über Realanteile (h-h id ) T,P
berechenbar
L.J. Gillespie, J.A. Beattie, Phys. Rev. 36, 743 (1930) (Ullmann)
46

A + B 2 C
Chemisches Gleichgewicht
dG =- SdT +VdP +Σ µ i dn i
Es gilt: -dn A =-dn B = 1/2 dn C
bzw. dn A = dn dn B ; C =- 2 dn A
dG = -SdT +VdP +(2µ - µ C A - µ B ) dn A
G weist ein Minimum für gegebene
Temperatur T und gegebenen Druck P
auf, wenn dG/dn A
= 0, d.h.:
µ A + µ B = 2µ C bzw. allgemein: Σ ν i µ i = 0
o f o
µ
i
= µ
i
+ RT ln = ∆g
B,i
+ RT
f
i
o
i
o
∑ ∑ ∑ ⎜ i
ν = = +
⎟ iµ
i
0 νi∆g
B,i
RT ln
o
⎝ fi
⎠
o
∆g R
ln
⎛
f
f
f
i
o
i
⎞
ν i
G
dG/dn A = 0
∆g
o
R
= −RT lnK
= −RT ln
⎛ f
⎜
⎝ f
A
o
A
⎛ f
⎜
⎝
⎞
⎟
⎠
C
o
fC
ν
A
⎞
⎟
⎠
ν
C
⎛ f
⎜
⎝ f
B
o
B
⎞
⎟
⎠
ν
B
n A
korrekte Gleichgewichtskonstante
47

Thermodynamische Grundlagen
aA + bB cC +
dD
Standardreaktionsenthalpie:
o
∆ = ∑
o
h
R
ν
i∆hB,
i
Kirchhoff:
K =
⎛
⎜
⎝
⎛
⎜
⎝
f
f
f
f
C
o
C
A
o
A
⎞
⎟
⎠
⎞
⎟
⎠
c
a
o
o
o
∆h R
( T ) = ∆hR
( To
) + ν
i
cP,
Chemisches Gleichgewicht:
⎛
⎜
⎝
⎛
⎜
⎝
f
f
f
f
D
o
D
B
o
B
⎞
⎟
⎠
⎞
⎟
⎠
d
b
T
∫∑
G = ! Minimum
= f (T )
T
o
i
a + bT + cT
dT
o
o
− RT ln K = ∆g R
= ∑ν
i∆g
B,
2
i
van’t Hoff:
o
d ln K ∆hR
=
2
dT RT
(
o
o
= Standardzustand für ∆g
)
f
i
B,
i
48

Darstellung von f i und f i
o
Darstellung der Fugazität f i
Weg A :
Weg B :
Standardfugazität :
f o
( T P)
f = y ϕ P
i i i
f = x γ f ≈
x γ P
o
s
i i i i i i i
f
( ) o s s
s
i
, i i
i
= ϕ
i
P
i
exp
v
c
P − P
RT
s
≈
P
i
o
∆g B
Standardfugazität der tabellierten - Werte bei 1 atm :
Gase (idealer Gaszustand) :
f o
i
= 1
atm
Flüssigkeiten, Feststoffe :
i i i
c
v i molares Volumen der Flüssigkeit bzw. des Feststoffes
f
o
s
= ϕ
P
s
exp
v
c
i
(
s
1atm
− P ) s
RT
i
≈
49
P
i

18.03.99
Thermodynamische Größen für den idealen Gaszustand
11 00 005 ChemEquil
50

Gleichgewichtsumsatz unabhängig von der Wahl des
Standardzustands
C 2 H 4 + H 2 O C 2 H 5 OH
Gibbssche Bildungsenthalpien
im Standardzustand:
C 2
H 4
∆g , kJ / mol
o,
id
B
68.11
∆g , kJ / mol
o , L
B
------
Dampfdruck Wasser bei 25 °C:
0.0312 atm
H 2
O
C 2
H 5
OH
-228.572
-168.28
-237.167
------
Standardzustand: ideales Gas ∆g Ro = -168.28 - 68.11 + 228.572 = -7.818 kJ/mol
fC H OH
/ 1atm
2 5
K
1
= 23.425 .
=
=
fC H
/ 1atm ⋅ fH O
/ 1atm
2 4 2
Standardzustand H 2 O: Flüssigkeit ∆g Ro = -168.28 - 68.11 + 237.167 = 0.777 kJ/mol
2 0.7309 = fC H OH
/ 1atm
2 5
K2
= 0.
7309
=
s
fC H
/ 1atm
⋅ fH O
/ P
2 4 2 H2O
K 1 = K 2 /P s H2O = 0.7309/0.0312 = 23.427
51

d ln K
dT
∆h
RT
Gleichgewichtsumsatz als f(T) für
R
endo- und exotherme Reaktionen 2
=
o
z.B. NH 3 ,
SO 3 , ..
z.B. Synthesegas-
Erzeugung
52

Maximaler und real erreichbarer Umsatz
für eine exotherme Reaktion
Zwischenkühlung,
z.B. Hordenreaktor
Kaltgaszugabe
53

Gleichgewichtsreaktion in der Gasphase
a A + b B c C + d D
K=
o c o d
( fC
fC
) ( f
D
f
D
)
o a o
( f f ) ( f f ) b
A
A
Annahme: ideales Gas Standardzustand für die tabellierten ∆g Bio
-Werte, d.h. f io
= 1 atm
Fugazität in der Gas( Dampf )-Phase per Definition:
K=
o c
o
( y ) ( )
Cϕ
CP
f
C
y
DϕDP
f
D
o a
o
( y ϕ P f ) ( y ϕ P f )
A
A
A
B
B
B
B
d
b
B
=
f i = y i ϕ i P = ϕ i P i
o c
o d
( P ) ( )
CϕC
f
C
PDϕ
D
f
D
o a
o
( P ϕ f ) ( P ϕ f ) b
Wenn für den Druck P ebenfalls die Einheit atm verwendet wird, ergibt sich:
A
A
A
B
B
B
K=
y
y
c
C
a
A
y
y
d
D
b
B
c d
ϕ ϕ
C D ⎛
a b
⎜
ϕ ϕ ⎝
A
B
P
1atm
⎞
⎟
⎠
Σν
i ν i
= K
y
K
ϕ
Σ
⎛ P ⎞
⎜ ⎟
⎝1atm
⎠
P
K=
P
c
C
a
A
P
P
d
D
b
B
c d
ϕ
Cϕ
D ⎛
a b
⎜
ϕ ϕ ⎝
A
B
1
1atm
⎞
⎟
⎠
Σν
i ν i
= K
P
K
ϕ
Σ
⎛ 1 ⎞
⎜ ⎟
⎝1atm
⎠
54

28.02.03
„Druckabhängigkeit“ der Gleichgewichtskonstante K P
Die Gleichgewichtskonstante einer chemischen Reaktion sollte
nur von der Temperatur abhängen
NH 3 -Synthese (450°C) 1/2 N 2 + 3/2 H 2 NH 3
K = K P K ϕ
P,atm 1 100 600 1000 1500 2000 3500
K P * 10 3 6.59 7.24 12.94 23.28 69.62 133.7 1075
Mit Hilfe der thermodyn. Standardgrößen und c P
id
: K = 6.62*10 -3
K ϕ
über Zustandsgleichung
P,atm 1 100 600 1000 …..
Kϕ 1.00 .914 0.512 0.284 …..
Reales Verhalten führt zu höheren Umsätzen, wenn Kϕ < 1
11 00 008 ChemEquil
55

28.02.03
„Druckabhängigkeit“ der Gleichgewichtskonstante K P
der NH 3 -Synthese bei 450°C
1.4
1.2
1
1/2 N 2 + 3/2 H 2 NH 3
K P atm -1
0.8
0.6
0.4
0.2
6.59 10 -3
0
11 00 008 ChemEquil
0 500 1000 1500 2000 2500 3000 3500
P, atm
56

K P
.10 -3
Einfluss der Gasphasenrealität auf den Gleichgewichtsumsatz der
Ammoniak - Synthese
K =
0
NH
3 3
0 0.5 0
( f / f ) ( f / f ) 1. 5
N
2
f
N
NH
Temperatur 450°C : K=6.62 . 10 -3
25.
20.
15.
10.
5.
exp. Daten:
Larson, A.T., Dodge, B.F.,
J.Amer.Chem.Soc. 1923,45,2918
Gillespie, L.J., Beattie, J.A.,
Phys.Rev. 1930,36,743
Ideales Gas
SRK (mit binären Parametern)
PSRK
VTPR
0.5N + 1.5H
NH
2
0. 200. 400. 600. 800. 1000.
/
f
H
2
2
H
2
P [atm]
2
(aus
Gleichgewichtsumsatz X
K
= KP
⋅ Kϕ
tabellierten
0.9
0.6
0.3
3
∆g
= e
0
B
0
R
∆g
−
RT
, ∆h
0
B
exp. Daten:
, c
0
P
Ideales Gas
−
Daten)
Larson, A.T., Dodge, B.F.,
J.Amer.Chem.Soc. 1923,45,2918
Gillespie, L.J., Beattie, J.A.,
Phys.Rev. 1930,36,743
SRK (mit binären Parametern)
PSRK
VTPR
0
0. 200. 400. 600. 800. 1000.
P[atm]
57

Umsatz der Ammoniak-Synthese als f(T, P)
58

Gleichgewichtsreaktion in der flüssigen Phase
a A + b B c C + d D
Annahme:
K=
o c o d
( f ) ( )
C
f
C
f
D
f
D
o
( ) a o
f f ( f f ) b
A
A
Standardzustand für die tabellierten ∆g Bi o -Werte die
reine Flüssigkeit bei einem Druck von 1 atm*, d.h.:
f i o = ϕ i s P i s Poy i * ≈ P i
s
Unter Verwendung der folgenden Beziehung für die
Fugazität in der flüssigen Phase bei P und T:
B
B
Poynting-Faktor Poy i
per Definition:
Poy
i
L s
v
i
(P − P
i
)
≈ exp
RT
Druck beim Standardzustand
( P = 1 atm ),
sonst P = Systemdruck
f i = x i γ i ϕ i s P i s Poy i ≈ x i γ i P i
s
c
ergibt sich vereinfacht: ( x γ ) ( )
C
x
Dγ
D
K=
a
( x γ ) ( x γ )
x
=
x
x
x
c d
γ
Cγ
D
a b
γ γ
d c d
C C D
=
b a b
A A B B A B A B
K
x
K
γ
Reales Verhalten
führt zu höheren
Umsätzen, wenn
K γ < 1
59

20.01.00
Umsatz bei der MTBE-Synthese
1.00
Umsatz XIsobuten
0.90
0.80
0.70
0.60
K=K x K γ
Methanol + Isobuten MTBE
Eduktverhältnis 1.06:1
P = 15 atm
(J.Chem.Eng.Data 37(1992)339)
0 20 40 60 80 100 120
Temperatur [°C]
ideal
UNIFAC
Exp. Daten
11 00 013a ChemEquil
60

Isobuten-Umsatz bei der MTBE-Synthese
mit
Butan
K
x
K γ
=
=
x
γ
x
MeOH
γ
MeOH
MTBE
x
MTBE
γ
i −Buten
i −Buten
61

18.03.99
Simultangleichgewichte, z.B. Synthesegaserzeugung
4 2 2 R
2 2 2 R
( )
( )
CH + H O CO + 3H ∆ h = 206.13kJ/mol 25°
C
CO + H O CO + H ∆ h = − 41.14kJ/mol 25°
C
11 00 014 ChemEquil
62

Ermittlung der Molmengen bei Simultangleichgewichten
(Beispiel: Gasphasenreaktion)
63

Die ersten Schritte der Relaxationsmethode
(Synthesegaserzeugung T =1100 K, P = 40 atm)
CH 4 + H 2 O CO + 3 H K
2
1 = 301 atm 2
CO + H 2 O CO 2 + H K
2
2 = 0.94
Schritt Reaktor n CH4
n H2O
n CO
n H2
n CO2
∆n i
Σ n i
1.00000 3.20000 0.00000 0.00000 0.00000 4.20000
1 1 0.34394 2.54394 0.65606 1.96818 0.00000 0.65606 5.51212
1 2 0.34394 2.22979 0.34191 2.28233 0.31415 0.31415 5.51212
2 1 0.33596 2.22181 0.34990 2.30627 0.31415 0.00798 5.52808
2 2 0.33596 2.22051 0.34859 2.30757 0.31545 0.00131 5.52808
3 1 0.33581 2.22035 0.34874 2,30803 0.31545 0.00015 5.52838
3 2 0.33581 2.22033 0.34872 2.30806 0.31548 0.00002 5.52838
4 1 0.33580 2.22033 0.34872 2.30807 0.31548

Die ersten Schritte der Relaxationsmethode
(Synthesegaserzeugung T =1100 K, P = 40 atm)
CH 4 + H 2 O CO + 3 H K
2
1 = 301 atm 2
CO + H 2 O CO 2 + H K
2
2 = 0.94
65

Die ersten Schritte der Relaxationsmethode
(Synthesegaserzeugung T =1100 K, P = 40 atm)
CH 4 + H 2 O CO + 3 H K
2
1 = 301 atm 2
CO + H 2 O CO 2 + H K
2
2 = 0.94
Anfangsmolmengen :
n = 1mol n = 1− ∆ n n = ∆n
CH ,0
CH CO
4 4
n = 3.2 mol n = 3.2 − ∆ n n = 3∆n
H O,0
H O H
2 2 2
∑
n
i
= 4.2 + 2∆n
3
∆ ( ∆ )
( − ∆ )( − ∆ )( + ∆ )
3 3 2 3 2 2
CO H2 CO H2 CO H2
2 2
CH4 H2O CH4 H2O
CH H O ( ∑ i )
4 2
p p y y P n n P n 3 n P
301= = = =
p p y y n n n 1 n 3.2 n 4.2 2 n
3 2
∆n( 3∆n)
P
( 1− ∆n)( 3.2 − ∆ n)( 4.2 + 2∆n)
⎛
⎞
F = 301− = 0 → ∆ n = 0.65606
⎜
2
⎟
⎝
⎠
2
66

Eindimensionales Suchverfahren: goldener Schnitt
d 1 - d
=
L d 1
1 1
d 1
= 0.61803... ∆n
allg.: d = 0.61803...
i
. di-1
F( ∆n)
0
0
d 1
d 1
∆n (L)
z.B. ∆n = 1 beim 1. Reaktor und
ersten Schritt der
Synthesegaserzeugung, 0.34394
(2.Reaktor, 1. Schritt)
F( ∆n)
d 2
d 2
0
0
∆n (L)
n-1
Ungewißheitsintervall: L
n=0.618..
67

Ermittlung der Gleichgewichtszusammensetzung einer
Isomerisierungsreaktion durch G-Minimierung
n-Butan i-Butan
Temperatur 25 ° C
Druck 1 atm.
Annahme : ideales Gas
Gibbssche
Standardbildungsgrößen bei 25°C:
∑
(
o
)
Komponente
∆g , J / mol
o
B
i-Butan (1) -20878
n-Butan (2) -17154
o
o
G = µ n µ = µ
+ RT lny P = ∆ g +
RT lny P
i
i i i i i Bi i
∑
d. h. G = n ∆ g +
RT lny P
i
i
i Bi i
Für 1mol und einemDruck P = 1atm
∑
(
o
ln )
g = y ∆ g +
RT y
i Bi i
68

Gibbssche Enthalpie für eine Isomerisierungsreaktion
Für 1mol und einemDruck P = 1atm
∑
i
(
o
ln )
g = y ∆ g +
RT y
z.B. y
1=0.1:
i Bi i
g = 0.1(-20878)+0.9(-17154)
( )
+8.31433⋅298.15
0.1ln0.1+0.9ln0.9
g= -18332J/mol
Konzentrationsverlauf der
Gibbsschen Enthalpie für das
System Isobutan (1) – n-Butan (2)
bei 25 °C und 1 atm
69

18.03.99
G
Minimierung der Gibbsschen Enthalpie
= ∑ µ n = Min.
i
i
!
o f o
µ
i
= µ
i
+ RT ln = ∆g
B,i
+
f
Annahme: ideales Gas (f i = p i )
Standardzustand ideales Gas (f io = 1atm)
i
o
i
RT ln
f
f
i
o
i
o
µ
i
= ∆gB,i
+ RT ln pi
nP
i
pi
=
∑n
j
( atm)
⎛
⎜
⎞
n P ⎟
5
o
i
F = ∑ni
∆ g
B,i(T) + RTln = Minimum
i
⎜
∑n
j ⎟
j
⎝
⎠
n i so wählen, dass F Minimum
aufweist. Jedoch muss auch
Nebenbedingung (Elementenbilanz)
erfüllt werden
11 00 021 ChemEquil
Ermittlung von G min durch nichtlineares Regressionsverfahren
(z.B. Simplex-Nelder-Mead) mit
Nebenbedingungen (Lagrangesche Multiplikatoren)
70

Beispiel:*
Berechnung der Lage des chemischen Gleichgewichts
durch Minimierung von G
Anfangsmolmengen:
Zielfunktion:
⎛
⎞
n P
F = n ⎜ ∆ g (T) + RTln ⎟ + 1− n − n − n
5
∑
i
4 2 2 R
*Annahme: ideales Gas
( )
o
i
i B,i CH4 CO CO
2
⎜
∑n
j ⎟
j
⎝
2 2 2 R
⎠
( )
( )
CH + H O CO + 3H ∆ h = 206.13kJ/mol 25°
C
CO + H O CO + H ∆ h = − 41.14kJ/mol 25°
C
n = 1mol; n = 3.2mol
CH4 H2O
2 2
( ) ( )
CH H O H O CO CO
+ 10.4 − 4n − 2n + 3.2 − n − n − 2n = Minimum
4 2 2 2
o
C
n = 1
o
H
n = 2 ⋅ 3.2 + 4 = 10.4
o
O
n = 3.2
Standardzustand, ideales Gas bei 1atm
2
71

18.03.99
Gleichgewichtskonzentrationen des Simultangleichgewichts des
Steamreforming-Verfahrens als Funktion der Temperatur bei 40 atm
( )
( )
CH + H O CO + 3H ∆ h = 206.13kJ/mol 25°
C
4 2 2 R
CO + H O CO + H ∆ h = − 41.14kJ/mol 25°
C
2 2 2 R
0.8
Molanteil
0.6
0.4
n
n
H 2 O
CH 4
= 3.2
CH4
H2O
CO
H2
0.2
CO2
11 00 023 ChemEquil
0
600 800 1000 1200 1400
Temperatur, K
72

11.02.99
Schema einer Vinylacetat-Anlage (vereinfacht)
C 2 H 4 + CH 3 COOH + ½ O 2
CH 3 COOCH=CH 2 + H 2 O
(exotherm)
101 01 016 Bedeutung
Nebenreaktionen, z.B.:
C 2 H 4 + 3 O 2 2 CO 2 + 2 H 2 O
(Acetaldehyd, Ethylacetat, .. )
73

Konzentration im Ausgangsgemisch / Verkaufspreis
74

Allgemeines Schema eines Trennprozesses
Trennhilfsmittel
Feed
Stufe
Ströme
unterschiedlicher
Zusammensetzung
Trennhilfsmittel
Energie
Zusatzstoff
Trennprozess
Rektifikation
Kristallisation
...
Absorption
Extraktion
Adsorption
Membrantrennverfahren
(Flüssig-Flüssig-,
Fest-Flüssig-,
überkritische Gase
Energie + Zusatzstoff
azeotrope und extraktive Rektifikation
75

11.02.99
Trennprozess und benötigtes Phasengleichgewicht
Trennprozeß Phase α Phase β Phase γ Gleichgewicht
Rektifikation Flüssigkeit Dampf - VLE
(vapor-liquid)
Rektifikation Flüssigkeit Flüssigkeit Dampf VLLE
(vapor-liquidliquid)
Absorption Flüssigkeit Gas (Dampf) - GLE
(gas-liquid)
Extraktion Flüssigkeit Flüssigkeit - LLE
(liquid-liquid)
Kristallisation Feststoff Flüssigkeit - SLE
(solid-liquid)
03 00 007 VLE
76

11.02.99
Zu berücksichtigende Aspekte bei der Auslegung von Trennprozessen
?
T
x 1
?
Rektifikation ? Kristallisation ?
α 12
=
γ
s
1 P1
≈ 1
?
γ
s
2 P2
Geeignetes Lösungsmittel
für die extraktive oder
azeotrope Rektifikation ?
y 1
x 1
?
Trennprobleme ?
AB A
C
Trenn-
Prozess ?
N th =?
Kolonnenhöhe ?
?
ABCD
?
S = n
[2(n-1)]!
n! (n-1)!
T n-1
101 01 012 Bedeutung
CD
B
D
Trennsequenz ?
78

11.02.99
Oxosynthese
Propylen + CO + H 2
HRh(CO)[P(C H SO Na) ]
6 4 3 3 3
(n / i)-Butyraldehyd
51 bar
125 °C
Reaktorauslegung:
Reaktionskinetiken
Gaslöslichkeiten
Verteilungskoeffizienten
LLE
VLE
Co-Solvents ?
55 bar
Kolonnenauslegung:
Gaslöslichkeiten
VLE
Phasen:
Gas / Dampf
organisch
wässrig
Propylen
CO + H 2
ungereinigtes
(n/i)-Butyraldehyd
79

Vorausberechnung des “Schicksals” einer Chemikalie in der Umwelt
KOW_vert.cdr
Luft
K = v · H / RT
Luft-Wasser
W
i,W
Aerosol
W
i
,W
i
s
= v · · P / RT
≈ (1/c )
i s,W ·
P / RT
i s
γ ∞ γ i
,W
K
Boden-Wasser
= 0.0082 KOW
Boden
K
Fisch-Wasser
= 0.045 KOW
=BCF
Sediment
Wasser
K
Sediment-Wasser
= 0.0164 KOW
K = = 0.1508 ·
OW
c i
O
c i
W
∞
γ
∞ ,O
i
80

Gleichgewichtsstufe – Typische Fragestellung
Theoretical Stage_d.cdr
Druck
Temperatur
bei einem
Typisches Problem
Dampf-Flüssig-Gleichgewicht :
Phase
Phase
β
β β
z 1, z 2, ....
α
α
α
z , z , ....
1 2
81

Dynamische
Apparatur
(NORMAG)
24.03.99
12 00 011 Exp. Best.
82

18.02.02
80
Isothermes Dampf-Flüssig-Gleichgewicht
des binären Systems Ethanol(1) - Wasser(2) bei 70°C
03 00 010 VLE
Druck P [kPa]
Siedelinie
70
60
50
Taulinie
40
T = 343.15 K
30
0.0 0.2 0.4 0.6 0.8 1.0
y 1 , x 1
x 1 y 1
P [kPa]
0.062 0.374 48.33
0.095 0.439 53.20
0.131 0.482 56.53
0.194 0.524 60.12
0.252 0.552 62.39
0.334 0.583 64.73
0.401 0.611 66.34
0.593 0.691 70.11
0.680 0.739 71.23
0.793 0.816 72.35
0.810 0.826 72.41
0.943 0.941 72.59
0.947 0.945 72.59
Mertl I., Collect.Czech.
Chem.Commun.,
37, 366-373, 1972
84

18.02.02
Anzahl der benötigten experimentellen Daten für ein System mit 10
Komponenten (∆x=0.1)
Art des Systems
(Anzahl
Komponenten)
Anzahl der
Systeme
Meßpunkte/
System
Gesamtzahl
Meßpunkte/
System
Gesamtzahl
Meßpunkte
1 10 1 10 10
2 45 9 405 415
3 120 36 4320 4735
4 210 84 17640 22375
5 252 126 31752 54127
6 210 126 26460 80587
7 120 84 10080 90667
8 45 36 1620 92287
9 10 9 90 92377
10 1 1 1 92378
Bei 10 Messpunkten pro Tag: Mehr als 37 Jahre für einen Druck (z.B. 1 atm)
03 00 017 VLE
87

18.03.99
Phasengleichgewichtsbeziehungen für VLE
Ausgehend von der Gleichgewichtsbedingung:
Gibbs: µ iα = µ iβ = µ iγ = .....
Lewis: f iα = f iβ = f iγ = .....
und der Definition der Hilfsgrößen γ ι und ϕ i :
γ
i
≡
f
x
L
i
o
ifi
L
ϕ i
≡
f
x
L
i
i
P
V
ϕ i
≡
f
y
V
i
i
P
erhält man für das Dampf-Flüssig-Gleichgewicht (VLE):
f =
L
i
f
V
i
L
V
A:
xϕ
P = y ϕ P
B :
i i i i
o
xγ f =
i
i
i
V
yϕ
P
i
i
03 00 018 VLE
88

11.02.99
Möglichkeiten zur Berechnung von Dampf-Flüssig-Gleichgewichten
WegAWegB.cdr
Weg A
f i L = f V i
Weg B
xi ϕi L P = yi ϕ V
i P
x γ f 0 = y
i i i i
ϕ
v
i
P
ln
ϕ
i
=
1
RT
∞
∫
v
⎡
⎛
∂P
⎞
⎢
⎜
⎟
⎢
⎝
∂
n
⎠
⎣
i T ,v,
n
j
RT
⎤
Pv
− ⎥
dv
−
ln
v
⎥
RT
⎦
Standardzustand:
reine Flüssigkeit
bei T und P:
vereinfacht:
x γ ϕ S P Poy = y ϕ P
i i i i s i i
v i
x γ P S = y P
i i i i
benötigt:
benötigt:
1) Zustandsgleichung für die Berechnung
des PVTn i - Verhaltens beider Phasen:
Soave-Redlich-Kwong
Peng-Robinson
...
03 00 024 VLE
1) Ausdruck für γ (T, P, n )
i
a) gE-Modell (g E = RT x i ln γi) :
Wilson, NRTL, UNIQUAC, ...
b) Gruppenbeitragsmethode:
UNIFAC, Mod. UNIFAC (Do), ...
2) Zuverlässige Mischungsregeln 2) P (T) (z.B. Antoine, Wagner)
i S
i
Σ
89

28.04.99
Gibbssche Mischungsenthalpie ∆g
Für konstante Temperatur gilt:
∆g=RT
∑
i
x lna
i
i
∑
∑
∆g=RT ⎡
⎣
x
i ilnx i+ x
i ilnγ
⎤
i ⎦
E
g 1
d.h.
∆g
= ∆g ideal
+ ∆g real
∆g
ideal
= RT
∑
i
x
i
ln x
i
g E E
g 2
∑
∑
∆ g = g = x g =
RT x ln γ
E
E
real i i i i i i
0 0.5 1
RT
lnγ
i
E
⎛
∂G
⎞
= ⎜
⎟
=
⎝
∂ni
⎠
T , P,
n
j
g
E
i
g
E
i
x 1
= RT lnγ
i
03 00 026 VLE
90

06.01.00
Ermittlung von Aktivitätskoeffizienten und Werte der Gibbsschen
Exzessenthalpie aus experimentellen VLE-Daten bei 70°C
s
x γ P =
i i i
y P
i
γ
i
=
yiP
x P
i
s
i
γ ∞
1
Ethanol (1)
Wasser (2)
70 o C, Mertl. et al.
γ ∞
2
g
E
RT
= Σ x lnγ = Σx
i i i
g
E
i
RT
x 1 y 1 P [kPa] T [K] γ 1 γ 2 g E /RT
343.15
343.15
343.15
...... ...... ...... ......
→
...... ...... ......
0.062 0.374 48.32 353.15 → 4.041 1.038 0.1211
0.095 0.439 53.18 353.15 → 3.407 1.061 0.1698
0.131 0.482 56.51 353.15 → 2.883 1.084 0.2087
g 2 E /RT
ln γ 2
ln γ 1
g 1 E /RT
03 00 027 VLE
91

11.02.99
Einfache g E -(Aktivitätskoeffizienten)-Modelle
RT
lnγ
i
=
⎛ ∂G
⎜
⎝ ∂n
E
i
⎞
⎟
⎠
T , P,
n
j
=
g
E
i
G
E
=
H
E
−TS
E
Randbedingung: g E = 0 für x i =1
Einfachstes g E -Modell: Porterscher Ansatz*
2
RT ln γ 1 = A x 2
g E = A x 1 x 2
2
RT ln γ 2 = A x 1
Flexibles g E -Modell: Redlich-Kister-Expansion
g E = x 1 x 2 [ A + B (x 1 - x 2 ) + C (x 1 - x 2 ) 2 + ..... ]
03 00 028 VLE
* A.W. Porter, Trans. Faraday Soc. 16, 336-345 (1921)
92

23.04.99
Entwicklung von g E -Modellen
Ideale Mischung (h E = 0, s E = 0, v E = 0)
∆g
=
RT
∑
x
i
E
g
ln xi
→ = 0
RT
Flory – Huggins (h E = 0, s E ≠ 0, v E = 0)
φ i = Volumenanteil der Komponente i
03 00 029 VLE
∆g
=
RT
∆g
=
RT
E
g
φi
lnφ xi
ln
RT x
∑ x → = ∑
i i
Wilson (1964) (h E ≠ 0, s E ≠ 0, v E = 0)
ξ i = lokaler Volumenanteil der Komponente i
E
g
ξi
lnξ xi
ln
RT x
∑ x → = ∑
i i
i
i
93

02.02.05
Wilson (1964)
Λ
12
=
v 2 ⎛ ∆λ12
⎞ v1
⎛ ∆λ
exp⎜
− ⎟;
Λ = exp⎜
−
21
21
v1
⎝ RT ⎠ v
2 ⎝ RT
⎞
⎟
⎠
Λ
2
1 1
1
2 2
2
ij
=
v
v
j
i
g
E
/ RT
= ∑ i
x
i
ξi
ln
x
⎡ λij
− λii
⎤
⎢−
⎥
⎣ ⎦
= v
exp
RT v
1
1 2
2
2 2
1
j
i
i
⎡
exp⎢−
⎣
∆λij
⎤
RT
⎥
⎦
v i molares Volumen der reinen Flüssigkeit i
∆λ ij Wechselwirkungsparameter zwischen
den Komponenten i und j (J/mol)
Wilson, G.M., J. Am. Chem. Soc. 86, 127 (1964)
ξ =
1
x
x
21
11
x
=
11
x
x
x11v
1
v + x
2
1
1
lnγ
1
= −ln
lnγ
2
= −ln
exp
exp
21
v
2
( − λ12
/ RT )
( − λ / RT )
11
⎛
ξ
2
x
x
12
22
=
=
x
12
x
x
x22v
2
v + x
1
2
1
exp
exp
g E
= −x1ln( x1
+ Λ12x2)
− x2
ln( Λ21x1
x2)
RT
+
22
v
2
( − λ21
/ RT )
( − λ / RT )
12
21
( x ) ⎜
⎟ 1
+ Λ12x2
+ x2
−
⎝ x1
+ Λ12x2
Λ21x1
+ x2
⎠
⎛
12
21
( x ) ⎜
⎟ 2
+ Λ21x1
− x1
−
⎝ x1
+ Λ12x2
Λ21x1
+ x2
⎠
Λ
Λ
22
Λ
Λ
⎞
⎞
03 00 031 VLE
E
g
RT
= −∑ x ln∑ x Λ
i
i
j
j
ij
lnγ
i
⎛
= −ln⎜
⎝
∑
j
⎞
x ⎟
jΛij
+ 1−
⎠
∑
k ∑
xkΛki
x Λ
j
j
kj
94

Ableitung der Wilson-Gleichung
E
g
ξ1 ξ2
= x1ln
+
x2
ln
RT x x
1 2
x11v
1
x22v
2
ξ1 = ξ
2
=
x v + x v x v +
x v
11 1 21 2 12 1 22 2
E
g
⎛ x v
⎞ ⎛ x v
⎞
11 1 22 2
= x1 ⎜ ln
⎟ +
x2
⎜ ln
⎟
RT ⎝ x1x11v 1 + x1x21v 2 ⎠ ⎝ x2x12v1 +
x2x22v
2
⎠
( −
λ )
( −
λ )
( −
λ )
( −
λ )
x x exp / RT x exp / RT
21 2 21 x12
1 12
= =
x x exp / RT x x exp / RT
11 1 11 22 2 22
( −
λ RT )
( −
λ RT )
( −
λ RT )
( −
λ RT )
exp
21
/ exp
12
/
x1x21 = x2x11 x2x12 =
x1x22
exp / exp /
11 22
E
g
RT
mit
⎛ ⎞ ⎛ ⎞
⎜ ⎟ ⎜ ⎟
x v
x v
x
⎜ 11 1
ln
⎟ x
⎜ 22 2
= ln
⎟
1 +
2
⎜ exp ( −
λ / RT )
⎟ ⎜ exp ( λ / RT )
⎟
21 −
12
⎜ x1x11v 1 + x2x11v 2 x x v +
x x v
exp ( −
λ / RT )
⎟ ⎜ 1 22 1 2 22 2
exp ( −
λ / RT )
⎟
⎝ 11 ⎠ ⎝ 22
⎠
( λ − λ ) ∆λ
( λ − λ )
v ⎛
2 12 11
⎞
2 12 1 21 22 1 21
12 21 12
exp v ⎛ ⎞
exp .: v ⎛ ⎞
bzw
21
exp v ⎛ ∆λ
⎞
λ = λ Λ = ⎜ − ⎟ = ⎜ − ⎟ Λ = ⎜ − ⎟ = exp ⎜ − ⎟
v1 ⎝ RT ⎠ v1 ⎝ RT ⎠ v2 ⎝ RT ⎠ v2
⎝ RT ⎠
( λ − λ ) v
− ( λ −
λ )
E
g
⎛ v
⎛ ⎞ ⎞ ⎛ ⎛ ⎞
⎞
2 21 11 1
12 22
= − x1 lnx + x exp ⎜ − ⎟ − x lnx +
x exp
⎜ ⎟
RT ⎜ 1 2 v RT ⎟ 2 ⎜ 2 1
v RT
⎟
⎝ 1 ⎝ ⎠ ⎠ ⎝ 2
⎝ ⎠
⎠
E
g
( ) ln( )
x ln x x x x x
RT = − + Λ − Λ +
1 1 2 12 2 1 21 2
95

11.02.99
Druckverlauf im ternären System Aceton(1)-Chloroform(2)-Methanol(3)
Aceton (1)
Chloroform (2)
Methanol (3) Weitere „local composition“-Modelle:
640
P [mmHg]
NRTL (non random two liquid theory) (1968)
Parameter: ∆g 12 , ∆g 21 , α 12
UNIQUAC (universal quasichemical theory) (1975)
Parameter: ∆u 12 , ∆u 21 , (van der Waalssche Größen r i , q i )
P calc [mm Hg]
600
560
520
480
440
400
400 440 480 520 560 600 640
P exp [mm Hg]
03 00 036 VLE
Wilson, ϑ = 50°C
Goral M., Kolasinska G., Oracz P., Warycha S.,
Fluid Phase Equilib., 23, 89-116, 1985
96

Erforderlich zur Anpassung zuverlässiger g E -Modellparameter
• Zuverlässige VLE-Daten (eventuell auch γ ∞ (T), h E , ...)
• Nichtlineare Regressionsmethode ( e.g. Simplex-Nelder-
Mead, ...)
• Geeignete Zielfunktion, z.B.
1
2 !
F = ∑∑( X
cal, i, j
− X
exp, i,
j ) = Min
n
1
!
F = ∑∑ X
cal, i, j
− X
exp, i,
j
= Min
n
F
1 ⎡ X
!
cal, i, j
− X ⎤
exp, i,
j
= ∑∑ ⎢
⎥ = Min
n ⎢⎣
X
exp, i,
j ⎥⎦
2
F
1 X
!
cal, i, j
− X
exp, i,
j
= ∑∑
= Min
n X
exp, i,
j
oder Kombinationen davon.
• Verwendung der experimentellen Reinstoffdampfdrücke von
großer Bedeutung!
97

SIMPLEX-Nelder-Mead-Methode
z.B.:
Die Zahlen geben Werte
der Zielfunktion F(x) an
F
=
∑
i
Komp
∑
j
Daten
( ) γ − γ
2
i, j,ber
i, j,exp
343.15 K
x 1
γ 1,exp
γ 2,exp
∆λ 1 2
∆λ
2 1
γ 1
∞
0.062 4.041 1.038
0.095 3.407 1.061
γ i
γ 2
∞
0.131 2.883 1.084
..... ....... .......
x 1
Nelder J.A., Mead R., Comp. J. 7,308 (1965)
Simplex2g.cdr
98

Dortmunder Datenbank (DDB)
bisher nur
10 – 15 %
publiziert
99

03.02.03
VLE Dataset (DECHEMA
Chemistry Data Series)
log 10
s
B
Pi
[ mm Hg]
= A −
ϑ ° + C
[ C]
Appendix:
v 1 = 58.69 cm 3 /mol
v 2 = 18.07 cm 3 /mol
r 1 =2.1055 q 1 =1.972
r 2 =0.9200 q 2 =1.400
03 00 042 VLE
cal/mol
A12
= ∆λ
oder ∆g oder ∆u
12 12 12
100

Flussdiagramm Bubble-T (Wilson)
Ethanol(1) – Wasser(2) Wilson
T= 343.15 K x 1
= 0.252 P, y 1
= ?
P 1s
( Antoine ) = 542.3 Torr
v 1
= 58.69 cm 3 /mol
∆λ 12
= 471.04 cal/mol
Λ 12
P 2s
= 233.17 Torr
v 2
= 18.07 cm 3 /mol
∆λ 21
= 883.75 cal/mol
= v 2
/v 1
exp (-∆λ 12
/RT)
= 18.07/58.69 exp ( - 471.04/(1.98721 343.15))
Λ 12
= 0.1543
Λ 21
= 0.8887
lnγ
1
= −ln
12
21
( x ) ⎜
⎟ 1
+ Λ12x2
+ x2
−
⎝ x1
+ Λ12x2
Λ21x1
+ x2
⎠
ln γ 1
= - ln ( 0.252 + 0.1543 0.748) +
0.748 ( 0.1543/(0.252 + 0.1543 0.748) –
( 0.8887/(0.8887 0.252 + 0.748))
ln γ 1
= 0.63144 γ 1
= 1.880 γ 2
= 1.165
P = 0.252 1.880 542.3 + 0.748 1.165 233.17
P = 256.96 + 203.25 = 460.2 Torr
y 1
= 256.96/460.2 = 0.5583
⎛
Λ
Λ
⎞
Input: x i , T
Parameter für
g E , P i
s
Berechnung
von γ i , P i
s
Berechnung
von P, y i
P = Σx i γ i P i
s
y i = x i γ i P is /P
Output: P, y i
102

11.02.99
Phasengleichgewichtsdiagramme für unterschiedlich stark reales Verhalten
Benzol(1)-
Toluol(2)
Methanol(1)
-Wasser(2)
Propanol(1)-
Wasser(2)
03 00 044 VLE
103

11.02.99
Verschiedene Phasengleichgewichtsdiagramme
1-Butanol(1)-
Wasser(2)
Aceton(1)-
Chloroform(2)
03 00 045 VLE
104

Überblick über die verfügbaren und benötigten VLE ( h E , γ∞) Daten
für binäre Systeme
Benötigte VLE-Daten im Rahmen der Prozessentwicklung:
1000 (500) Komponenten von technischem Interesse
VLE-Daten für ca. 500 000 (125 000) binäre Systeme erforderlich.
Verfügbare Daten:
1 VLE Datensatz (10240 Systeme) : 2.05 % (8.20 %)
> 1 VLE Datensatz (6140 Systeme): 1.23 % (4.91 %)
1 VLE Datensatz + 1 h E + 1 γ∞ (996 Systeme): 0.20 % (0.80 %)
> 1 VLE Datensatz + 1 h E + 1 γ∞ (767 Systeme): 0.15 % (0.61 %)
Status der Dortmunder Datenbank (VLE, h E , γ∞) (Sept. 2007) :
DDB
VLE
53 700 isotherme / isobare Datensätze
γ∞
49 700 Datenpunkte in reinen
Lösungsmitteln
h E
18 100 Datensätze

Gruppenbeitragsmethoden (z.B. UNIFAC)
Ethanol:
n-Hexan:
-OH -CH 3
-CH 2 -CH 2 -CH 2
-CH 2 -OH
-CH 3 -CH 2
-OH
-CH 3 -CH 2
-CH 2 -CH 2 -CH 2 -CH 3
ln γi = ln γi C + ln γi R
ln γ C i = f(x i, q i, r i)
r =
ln γ = ν (lnΓ - ln Γ )
i R
Ψ nm
q =
i
i
Σ ν
Σ ν
Σ
(i)
k
(i)
k
Q
R
k
k
k (i) k k (i)
= exp (-a nm
/ T)
106

UNIFAC Matrix (Dezember 2007)
UNIFAC Parameter Matrix
December 2008
New Structural
Groups:
51 NCO
52 Epoxides
53 Anhydrides
54 Carbonates
55 Sulfones
56 HCONR
57 ACCN
58 Lactames
59 Lactones
60 Peroxides
61 Acetals
62 ACNR2
63 ACNHR
64 ACBr
65 Oxime
66 Furane
67 PO4
08 00 006 GC-gE
Hansen et al., Ind. Eng. Chem. Res.
30, No.10, 2352-2355 (1991)
1
1 CH 2
2
2 C=C
3
3 ACH
published parameters
4
4 ACCH 2
5
5 OH
6
6 CH OH
3
7
7 H 2
O
8
8
9
delivery 1998
ACOH
9 CH 2CO
10
10 CHO
11
11 CCOO
12
12 HCOO
13
13 CH 2 O
delivery 1999
14
14 CH 2NH
2
15
15 CH 2NH
16
16 (C)3N
17
17 ACNH 2
delivery 2000
18
18 Pyridin
19
19 CH CN
2
20
20 COOH
21
21 CCl
22
22 CCl 2
23
23 CCl 3
delivery 2001
24 CCl
24
4
25
25 ACCl
26
26 CNO 2
27
27 ACNO 2
28
28 CS 2
delivery 2002
29
29 CH 3SH
30
30 Furfural
31
31 DOH
32
32 I
33
33 Br
34 delivery 2003
34 C C
35
35 DMSO
36
36 Acryl
37
37 ClC = C
38 ACF
38
39 DMF
39 delivery 2004
40 CF
40
2
41 COO
41
42
42 SiH 2
43
43 SiO
44
44 NMP
45
45 CClF
46
46 CON
47 OCCOH
47
48
48 CH2S
49
49 Morpholin
50
50 Thiophen
51 NCO
51
52
52 Epoxy
53 Anhydrides
53
54 Carbonates
54
55 Sulfones
55
56 HCONR
56
57
57
ACCN
58
58 Lactames
59
59 Lactones
60
60 Peroxides
61
61 Acetals
62
62 ACNR2
63
63 ACNHR
64
64 ACBr
65
65 Oxime
66
66 Furane
67
67 PO 4
delivery 2005
delivery 2006
delivery 2007
new or revised parameters,
delivery 2008
no parameters
available
108

Abschätzung von Aktivitätskoeffizienten
UNIFAC-Wechselwirkungsparametermatrix
a nm
(K) einiger ausgewählter Strukturgruppen
Hauptgruppe 1 2 3 4 5 6 7 8 9
1 CH 2 0.0 86.02 61.13 76.5 986.5 697.2 1318.0 1333.0 476.4
2 C=C -35.36 0.0 38.81 74.15 524.1 787.6 270.6 526.1 182.6
3 ACH -11.12 3.446 0.0 167.0 636.1 637.35 903.8 1329.0 25.77
4 ACCH 2 -69.7 -113.6 -146.8 0.0 803.2 603.25 5695.0 884.9 -52.1
5 OH 156.4 457.0 89.6 25.82 0.0 -137.1 353.5 -259.7 84.0
6 CH 3 OH 16.51 -12.52 -50.0 -44.5 249.1 0.0 -180.95 -101.7 23.39
7 H 2 O 300.0 496.1 362.3 377.6 -229.1 289.6 0.0 324.5 -195.4
8 ACOH 275.8 217.5 25.34 244.2 -451.6 -265.2 -601.8 0.0 -356.1
9 CH 2 CO 26.76 42.92 140.1 365.8 164.5 108.65 472.5 -133.1 0.0
10 CHO 505.7 56.3 23.39 106.0 -404.8 -340.18 232.7 - 128.0
11 CCOO 114.8 132.1 85.84 -170.0 245.4 249.63 200.8 -36.72 372.2
12 CH 2 O 83.36 26.51 52.13 65.69 237.7 238.4 -314.7 - 191.1
13 CNH 2 -30.48 1.163 -44.85 - -164.0 -481.65 -330.4 - -
14 ACNH 2 1139.0 2000.0 247.5 762.8 -17.4 -118.1 -367.8 -253.1 -450.3
15 CCN 24.82 -40.62 -22.97 -138.4 185.4 157.8 242.8 - -287.5
16 COOH 315.3 1264.0 62.32 268.2 -151.0 1020.0 -66.17 - -297.8
17 CCl 91.46 97.51 4.68 122.91 562.2 529.0 698.24 - 286.28
18 CCl 2 34.01 18.25 121.3 140.78 747.7 669.9 708.7 - 423.2
19 CCl 3 36.7 51.06 288.5 33.61 742.1 649.1 826.76 - 552.1
20 CCl 4 -78.45 160.9 -4.7 134.7 856.3 860.1 1201.0 10000.0 372.0
21 ACCl -141.26 -158.8 -237.68 375.5 246.9 661.6 920.4 - 128.1
109

Dampf- Flüssig- Gleichgewichte von Alkan-Keton-Systemen
alkan_keto_UNIFAC.cdr, 23.11.2000
1.0
y 1
0.5
n-Octan +
Cyclopentanon
(90°C)
Cyclohexan +
Cyclohexanon
(75°C)
n-Heptan +
3-Pentanon
(65°C)
0.0
0.5
0.0
y 1
y 1
x 1 x 1
2-Butanon +
n-Octan
(65°C)
2-Butanon +
Cyclohexan
(1 atm)
n-Hexan +
2-Butanon
(60°C)
Experimentelle und nach der UNIFAC-
Methode berechnete Dampf-Flüssig-
Gleichgewichte binärer Kohlenwasserstoff-Keton-Systeme
UNIFAC
experimentell
0.5
Aceton +
Cyclohexan
(1 atm)
Aceton +
n-Hexan
(20°C)
2-Methylbutan +
Aceton
(1 atm)
0.0
0.0 0.5 0.0 0.5 0.0 0.5 1.0
x 1
110

Mitglieder des UNIFAC Konsortiums (Mai 2008)

Verlauf der Isothermen einer kubischen Zustandsgleichung
⎛ ∂P
⎞
⎜ ⎟
⎝ ∂v
⎠
T
2
⎛ ∂ P
=
⎜
2
⎝ ∂v
⎞
⎟
⎠
kr T kr
=
0
Siedelinie
Taulinie
113

P rep
rep
P = P +
=
van der Waals-Zustandsgleichung (1873)
(Nobelpreis für Physik 1910)
P
att
RT
v − b
P
att
=
−
a
v
• a - intermolekulare Anziehung
• b - Volumen der dichtesten Packung
2
v
3
⎛
− ⎜b
⎝
+
RT
P
⎞
⎟v
⎠
2
+
a
P
v
−
ab
P
114
=
0

11.02.99
Ermittlung von a und b aus kritischen Daten
02 01 016 PvT
P RT a
= − v 2
− b v
am kritischen Punkt gilt:
⎛ ∂P ⎞ RT 2a
⎜ = − + = 0
2 3
v
⎟
⎝ ∂ ⎠ − v
T
kr
( v b)
2
⎛ ∂ P ⎞ 2RT 6a
⎜ 2 ⎟ = - = 0
3 4
⎝ ∂v
⎠T
( v - b)
v
kr
daraus folgt:
RT
kr
( v − b)
kr
2RT
kr
( v − b)
kr
=
2a
v
2 3
kr
=
6a
v
3 4
kr
nach Division und Substitution:
a
9RT v
kr kr
kr
=
8
v
3
damit erhält man für P kr
:
P
die allgemeine Form lautet also:
bzw. nach Division durch P kr
bzw. 3 R T kr
/ 8 v kr
b
=
RT 9RT v 3RT
= − =
kr kr kr kr
kr 2
vkr − vkr 3 8vkr 8vkr
P RT 9 8 RTkr
v
= − v v 3 v 2
−
kr
P 8T 3
= − 3v 1 v
r
r 2
r
−
r
kr
T P v
Tr = Pr = vr
=
T P v
115
kr kr kr

Messung kritischer Punkte am Beispiel von Ethan
H 2
O:
T kr = 647.3 K
P kr = 220.4 bar
T kr - 0.5 K
T kr = 305.41 K
T kr + 0.5 K
116

Der azentrische Faktor ω
1
117

Die perfekte Zustandsgleichung – aber wie?
Perfecteos_d.cdr
P
A New Equation
of State
KEY
α
ρ (P,T)
T
c
χ
P
z c
c
ω
v c
∂P
∂v
2
∂ P
2
∂v
Tc
Tc
z = z c!
= 0
= 0
EXPTL.
PRESENT
STUDY
v
118

09.01.00
Otto Redlich, John M. Prausnitz, Jürgen Gmehling
RT
v −b
P = −
1/
2
T
a
v
( v + b)
05 00 001b EOSMIX
119

Giorgio Soave
P
=
RT
v −
b
−
v
a ( T )
( )
v
+
b
Peng-Robinson-Zustandsgleichung:
P =
RT
v − b
−
v
a( T)
( v + b) + b( v − b)
log (P r
s )
experimentelle Werte
für Ethanol
RK
SRK
T kr
= 516.2 K
P kr
= 63.83 bar
ω = 0.635
Soave-Redlich-Kwong Gleichung (SRK)
1/T r

11.02.99
P-x(y)-Diagramm für das System Stickstoff (1) + Methan (2)
Zustandsgleichung: Soave-Redlich-Kwong; k 12 = 0.03014
177.59 K
166.48 K
144.26 K
133.15 K
Mischungsregeln:
b = Σz i
b i
a ij =(a ii
a jj ) 0.5 (1-k ij )
a = Σ Σz i z j a ij
110.93 K
05 00 008 EOSMIX
121

Definition von Realanteilen:
Berechnung von Realanteilen
m R ≡ (m-m id ) T,P
Realanteil ist die Differenz aus realem Wert und dem Wert bei gleichem Druck
und gleicher Temperatur im idealen Gaszustand:
Beispiele:
Volumen:
Gibbssche Enthalpie:
RT
P
id
( v − v ) = ( z 1)
T, P
−
⎡⎛
∂g
⎞
⎢⎜
⎟
⎣⎝
∂P
⎠
⎛ ∂g
⎝ ∂P
id
P
id
( g − g ) = ∫ − ⎜ ⎟ dP
T,
P
0
T
⎞
⎠
T
⎥ ⎦
⎤
RT⎤
P ⎥ ⎦
P
id
( g − g ) = ∫ v − dP
T,
P
0
⎡
⎢
⎣
122

20.02.03
Gleichungen zur Berechnung von Realanteilen
volumenexplizite
Zustandsgleichung
druckexplizite
Zustandsgleichung
RT
ln ϕ ≡
id
( g − g ) T, P
(
id
h −h ) T, P
P
∫
0
P
∫
0
⎛
⎜v
−
⎝
RT
P
⎞
⎟ dP
⎠
⎡ ⎛ ∂v
⎞
⎢v
−T
⎜ ⎟
⎣ ⎝ ∂T
⎠
P
⎤
⎥dP
⎦
v
∫
∞
⎛
⎜
⎝
RT
v
⎞
− P ⎟dv
+ RT(z −1−
ln z)
⎠
v
⎡ ⎛ ∂P
⎞
− ∫ ⎢P
−T
⎜ ⎟
⎣ ⎝ ∂T
∞ ⎠v
⎤
⎥dv
+ Pv − RT
⎦
(
id
s − s ) T, P
P
∫
0
⎡
⎢−
⎣
⎛
⎜
⎝
∂v
∂T
⎞
⎟
⎠
P
+
R ⎤
⎥dP
P ⎦
v
∫
∞
⎡⎛
∂P
⎞
⎢⎜
⎟
⎣⎝
∂T
⎠
v
−
R
v
⎤
⎥dv
⎦
+ R ln z
P
⎛
( ) ∫ ⎟ ⎞
⎜
∂ 2
id
v
cP
− cP
= −T
T,P
2
⎝ ∂T
0 ⎠
P
dP
∞
id
(
v
− cv
) = −T
T,P ∫
2
⎛ ∂ P ⎞
⎜
⎟
⎝ ∂T
⎠
c
2
v
v
dv
123

Berechnung der Enthalpie über Realanteile
h
Referenzzustand
id
h (T)
0,id id
= h + c dT
T
∫
∆ 0 B
P
T 0
V id
(h - h )
T 1 ,P s
VerdampfungsenthalpienEOS.cdr
0,id
∆h B
∆h (T )
v 1
L id
(h - h )
T 1
,P s
T 0
T 1
T
T kr
124

Einfluss des Druckes auf die Reaktionsenthalpie
realer Gase
Druck
P
III
II
∆hR ( T,P)
T = konstant
I
(
o
)
o
R I II III
∆ h T,P = ∆ h + ∆ h + ∆h
I
II
Edukte
R
(
id
)
∆ h = ν h − h
( )
∆ h = ∆h T,P
Edukte,T,P
ideales Gas
(1 atm)
Produkte
o
R
( )
∆h T,P
IV
Edukte
III
Pr odukte
(
id
)
∆ h = ν h − h
Pr odukte,T,P
Enthalpie
o
R R i
( ) (
id
)
∑
∆ h (T,P) = ∆ h T,P + ν h − h
i,T,P
125

Druckeinfluss auf die Reaktionsenthalpie: Ammoniaksynthese (450°C)
0.5 N 2 + 1.5 H 2 NH 3
Standardreaktionsenthalpie (ideales Gas) ∆h Ro = - 52 878 J/mol
Fragestellung: Reaktionsenthalpie bei 600 atm?
VTPR
N 2
H 2
NH 3
id
( h − h )
450 ° C, 600 atm
815 J/mol
1 152 J/mol
- 4 896 J/mol
Referenzzustands-
Gleichungen
945 J/mol
1037 J/mol
-5032 J/mol
∆h R (600 atm) = - 52 878 – 0.5 . 815 – 1.5 . 1152 – 4896 = - 59 909 J/mol
L.J. Gillespie, J.A. Beattie, Phys. Rev. 36, 743 (1930) (Ullmann): - 59 650 J/mol
126

Druckabhängigkeit der Reaktionsenthalpie
am Beispiel der Ammoniaksynthese
450 °C
∆hR [kJ/mol]
-55
-62
0 200 400 600 800
Druck [atm]
- - - VTPR
_____
Referenzzustandsgleichung
__ __ __
Ullmann (Ammonia)
127

Mögliche Anwendungsbeispiele bei Kenntnis des realen Verhaltens
Synthese thermischer Trennprozesse
Berechnung von
(Auswahl selektiver Zusatzstoffe,
Phasengleichgewichten
Festlegung Trennsequenz, ...)
(VLE, LLE, SLE, GLE, ...)
Auslegung von
Trennkolonnen (N ) th
applic_d.cdr
Berechnung von
Chemisches
Exzeßgrößen
Gleichgewicht (K γ, K ϕ)
(h E, c P E , v E , ...)
Sicherheitsfragen
Kenntnis des
Standardbildungsgrößen
( ∆h B o , ∆g B o ) verhaltens ( γi, ϕi, PVT)
(Flammpunkte, ...)
realen Gemisch-
gewünscht für
Umweltschutz
Analytik (GLC, ..)
(K OW → Ausbreitung,
Bioakkumulation, ...)
Arbeitsschutz (Sicherheitskleidung,
Exposition, ...)
diffusiver Stofftransport
reaktionskinetische Ansätze
(LM-Effekte, kinetische Ausdrücke, ...)
Berechnung thermodynamischer
Größen (h, s, ..., ∆h , ∆h (P), ...)
v
R
128