8 Flächenberechnung

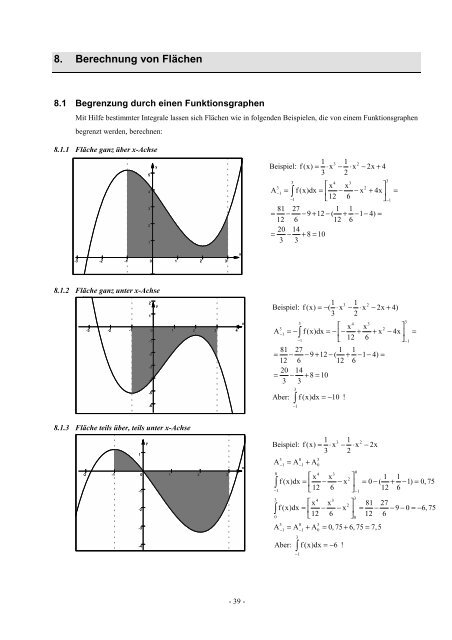
8. Berechnung von Flächen
8.1 Begrenzung durch einen Funktionsgraphen
Mit Hilfe bestimmter Integrale lassen sich Flächen wie in folgenden Beispielen, die von einem Funktionsgraphen
begrenzt werden, berechnen:
8.1.1 Fläche ganz über x-Achse
-3 -2
-1
0
1 2 3
8.1.2 Fläche ganz unter x-Achse
8.1.3 Fläche teils über, teils unter x-Achse
5
4
3
2
1
2
1
y
y
-3 -2
-1
0
1 2 3 4
1
y
-1
-2
-3
-4
-5
-6
-2 -1
0
1 2 3
-1
-2
-3
-4
x
x
x
- 39 -
1 3 1 2
Beispiel: f(x) = ⋅x− ⋅x− 2x + 4
3 2
3 4 3
3
3 ⎡x x 2 ⎤
−1
∫ ⎢ ⎥
12 6
−1 ⎣ ⎦−1
A = f(x)dx = − − x + 4x =
81 27 1 1
= − − 9+ 12 − ( + −1− 4) =
12 6 12 6
20 14
= − + 8= 10
3 3
1 3 1 2
Beispiel: f(x) =−( ⋅x − ⋅x − 2x+ 4)
3 2
3 4 3
3
3 ⎡ x x 2 ⎤
−1
∫ ⎢ ⎥
12 6
−1 ⎣ ⎦−1
A =− f(x)dx =− − + + x − 4x =
81 27 1 1
= − − 9+ 12 − ( + −1− 4) =
12 6 12 6
20 14
= − + 8= 10
3 3
Aber:
3
∫ f (x)dx =−10
!
−1
1 3 1 2
Beispiel: f(x) = ⋅x− ⋅x− 2x
3 2
3
A
0
= A
3
+ A
−1 −1
0
0 4 3
0
⎡x x 2 ⎤ 1 1
∫ f(x)dx= ⎢ − − x ⎥ = 0 − ( + − 1) = 0,75
−1 ⎣12 6 ⎦ 12 6
−1
3 4
⎡x 3
x
3
2 ⎤ 81 27
∫
f(x)dx= ⎢ −
⎣12 6
− x ⎥
⎦
= −
12 6
−9− 0=−6,75 A = A + A = 0,75+ 6,75= 7,5
0 0
3 0 3
−1 −1
0
3
Aber:
∫ f(x)dx=−6 !
−1

8.1.4 Fläche begrenzt durch Nullstellen
-3 -2
-1
0
1 2 3
8.1.5 Aufgaben
Übungsblatt Flächenberechnung: 1a) Integral
3
2
∫ (x x)dx
−1
- 40 -
16
− =
3
Nullstellen 0 und 1, Fläche A
Hausaufgabe: S. 180/1 Nullstellen 0 und 6 (doppelt)
6
1 2 6
∫ ⋅x ⋅(x− 6) dx = 27= A0
4
8.2 Flächen zwischen Funktionsgraphen
0
1 3 1 2 10
Beispiel: f(x) = ⋅x− ⋅x− 2x +
3 2 3
Nullstellenberechnung ergibt (vgl. §6 Hbsp):
x0 =− 2,5; x1 = 2
2 4 3
2
2 ⎡x x 2 10x⎤
−2,5
∫ ⎢ ⎥
−2,5 ⎣12 6 3 ⎦−2,5
A = f(x)dx = − − x + =
16 8 20 625 125 25
= − − 4 + − ( + −6,25 − ) =
12 6 3 192 48 3
45 375 375
=− 4+ − + 6,25= 17,25−
=
3 64 64
729
= ≈11,39
64
Die Fläche, die zwei Funktionsgraphen (Funktionen f und g) miteinander einschließen, ergibt sich mit dem
Integral über die Differenzfunktion f-g, wobei analog zu 7.1 f-g immer dasselbe Vorzeichen aufweisen muss.
Nullstellen der Funktionen f oder g beeinflussen das Ergebnis nicht!
8.2.1 Beispiel
Die Funktionen f:y 4
1
8
x
8.2.2 Aufgaben
5
4
3
2
1
-1
y
2
= − ⋅ und
5
4
3
2
1
y
1
g:y x
8
x
2
= ⋅ (vgl. §5, Aufgabe E)
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7
-1
-2
-3
-4
-5
3
− 1 =
17
3
Schnittstellen x1;2 =± 4
1
A = (f (x) − g(x))dx = (4 − ⋅ x )dx =
4 4
4
−4
∫
−4 ∫
−4
4
2
3
4
⎡ x ⎤ 64 64
= ⎢4x − ⎥ = 16 − −( − 16 + ) =
⎣ 12 ⎦ 12 12
−4
32 64
= 32 − = ≈ 21, 33
3 3
Übungsblatt Flächenberechnung: 2c) Schnittpunkte bei x02 =− (doppelt, d.h. Berührpunkt!) und x1= 1.
x

S. 180/3
2
f (x) =− 0,5x + 1,5x + 5 ; Nullstellen: x0 =−2 Tangente in (0|5): t(x) = 1, 5x + 5
∨ x1 = 5
A1
A2
1
∫
−2
(f (x) − g(x))dx = −6, 75 ⇒ A = 6, 75
Hausaufgabe:
S. 181/10 Schnittpunktsabszissen: x1 = 0 ∨ x2 =−2 ∨ x3 = 4
0 5 4
A1= A −2
= ; A2= A0 6
16
=
3
⇒
5 16 37
Ages = + = ≈ 6,17
6 3 6
8.3 Vermischte Aufgaben
- 41 -
1
−2
0
17
A2= ∫ f(x)dx =
3
−2
t(x) = 0 ⇒
10
x2 = −
3
⇒
1 10 25
A∆ = ⋅ ⋅ 5 =
2 3 3
25 17 8
A1 = − =
3 3 3
⇒ A 1 :A2 = 8:17
Übungsblatt Aufgabe 3:
Funktion g: Nullstellen x0 = 0 ∨ x1 = −7,5 ∉[ − 7;7] =D g ; H( −5|6, 25), T(0| 0), W( − 2, 5|3,125)
a 1 20
⇒ + = 0 ⇔ a =−
40 6 3
7
6
5
4
3
2
1
y
-4 -3 -2 -1 0 1 2 3 4 5
11 y
-7 -6 -5 -4 -3 -2 -1 0 1
10
9
8
7
6
5
4
3
2
1
3.1 Schnittpunkte mit Graphen von f:
S( 1 − 5|6,25) und S 2 (0| 0) (Berührpunkt)
3.2
A
0
3
∫ (0,1x
−5
2
0, 5x )dx
4 3
0
−5
∫
a
= + =
⎡x x ⎤ 125
= ⎢ + ⎥ =
⎣40 6 ⎦ 24
−5
125
(f (x) − g(x))dx =
24
−5
4 3
3 2
∫
a
125 125 a a 125
( −0,1x − 0,5x )dx = ⇔ + + =
24 24 40 6 24
Übungsblatt Aufgabe 4:
Der Graph von f schneidet die x-Achse bei x12 =− und x2= 2.
Wegen Achsensymmetrie zur y-Achse gilt:
x
x

2 2 3
2 2 ⎡ x ⎤
A = ∫ (4− x )dx = 2 ⋅∫ (4− x )dx = 2⋅⎢4x− ⎥
−2
0 ⎣ 3 ⎦0
8 32
= 2 ⋅(8 − ) =
3 3
⇒
A 4
=
8 3
Schnittpunkte des Graphen von f mit der Geraden y = a :
2
4− x = a ⇔ x1;2 = ± 4− a
4
2
- 42 -
Wegen Achsensymmetrie zur y-Achse beider
Graphen ergibt sich:
4−a ∫ (4
0
2
x a)dx
− − =
3
4−a ⎡ ⎤
2
1
x
x
= ⎢(4 −a) ⋅x− ⎥ =
⎣ 3 ⎦0
1
= (4−a) ⋅ 4−a − ⋅(4−a) ⋅
3
4− a =
-2 -1
0
1 2
2
= ⋅(4 −a) ⋅
3
4−a 2
Damit muss gelten: ⋅(4 −a) ⋅
3
2
4 − a =
3
⇔ (4 −a) ⋅ 4 − a = 1
2
⇒
3
(4 − a) = 1
⇔ 4− a = 1 ⇔ a = 3
Übungsblatt Aufgabe 5:
3 2
5.1) F(x) = x + 3x + C; F(1) = −4⇒ C = − 8
5.2 Nullstellen von f: x1 = 0 ∨ x2 = − 2;
3
y
−2
∫
0
(3x + 6x)dx = F( −2) − F(0) = 4 = A
2 0
−2
5.3 f ist die 1. Ableitung von H, d.h. mögliche relative Minima von H sind die Nullstellen ( x1 = 0 ∨ x2 = − 2)
der Funktion f!
H ′′ (x) = f ′ (x) = 6x + 6; H ′′ (0) = f ′ (0) = 6 > 0 ⇒ x1 = 0 rel. Minimum von H
3 2
3 2
Aus H(x) = x + 3x + C und H(0) = 1 ergibt sich: H(x) = x + 3x + 1