Wechselwirkung ionisierender Strahlung mit Materie
Wechselwirkung ionisierender Strahlung mit Materie
Wechselwirkung ionisierender Strahlung mit Materie
Sie wollen auch ein ePaper? Erhöhen Sie die Reichweite Ihrer Titel.
YUMPU macht aus Druck-PDFs automatisch weboptimierte ePaper, die Google liebt.
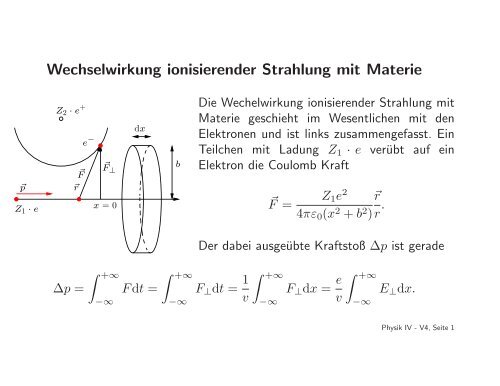
<strong>Wechselwirkung</strong> <strong>ionisierender</strong> <strong>Strahlung</strong> <strong>mit</strong> <strong>Materie</strong><br />
Z 2 · e +<br />
⃗F<br />
e −<br />
⃗F ⊥<br />
dx<br />
b<br />
Die Wechelwirkung <strong>ionisierender</strong> <strong>Strahlung</strong> <strong>mit</strong><br />
<strong>Materie</strong> geschieht im Wesentlichen <strong>mit</strong> den<br />
Elektronen und ist links zusammengefasst. Ein<br />
Teilchen <strong>mit</strong> Ladung Z 1 · e verübt auf ein<br />
Elektron die Coulomb Kraft<br />
⃗p<br />
Z 1 · e<br />
⃗r<br />
x = 0<br />
⃗F =<br />
Z 1 e 2 ⃗r<br />
4πε 0 (x 2 +b 2 ) r .<br />
Der dabei ausgeübte Kraftstoß ∆p ist gerade<br />
∆p =<br />
∫ +∞<br />
−∞<br />
Fdt =<br />
∫ +∞<br />
−∞<br />
F ⊥ dt = 1 v<br />
∫ +∞<br />
−∞<br />
F ⊥ dx = e v<br />
∫ +∞<br />
−∞<br />
E ⊥ dx.<br />
Physik IV - V4, Seite 1
Das Integral kann <strong>mit</strong> einem Trick berechnet werden. Der Satz von Gauß lautet<br />
ja ∫ ∫<br />
⃗E ·dA ⃗ = 2πb E ⊥ dx = Q/ε 0 = Z 1 e/ε 0 .<br />
Wir setzen dies oben ein und erhalten<br />
A<br />
∆p =<br />
∆ǫ = ∆p2<br />
2m e<br />
=<br />
1<br />
· Z1e 2<br />
2πε 0 vb , bzw.<br />
(<br />
1 Z1 e 2 ) 2<br />
8π 2 ε 2 0 m · .<br />
e vb<br />
Der zweite Ausdruck gibt die durch das Projektil-Teilchen an das untersuchte<br />
Target-Elektron übertragene Energie an. Nun müssen wir nur noch über<br />
alle möglichen Stoßparameter b integrieren um die <strong>Wechselwirkung</strong> <strong>mit</strong> allen<br />
Elektronen zu berücksichtigen. Wegen der Abschirmung der Ladung integrieren<br />
Physik IV - V4, Seite 2
wir von einem minimalen sinnvollen Stoßparameter b min bis zu einem maximalen<br />
sinnvollen Stoßparameter b max und erhalten<br />
( ∫ )<br />
bmax<br />
∆p 2<br />
dE = − n e 2π ·b·db ·dx, bzw.<br />
b min<br />
2m e<br />
dE<br />
dx = − Z2 1e 4 ( )<br />
n e bmax<br />
4π ·ε 2 ,<br />
0 v2 m e·ln<br />
b min<br />
wo n e die Elektronendichte entlang des Weges dx sei. Der spezifische<br />
Energieverlust dE/dx ist proportional zur Elektronendichte im Targetmaterial,<br />
steigt quadratisch <strong>mit</strong> der Kernladung des Projektils und nimmt umgekehrt<br />
proportional zum Quadrat der Geschwindigkeit des Projektils ab.<br />
Die Bestimmung von b max und b min ist nun wesentlich komplizierter. Sie hängen<br />
von der Geschwindigkeit v des Projektils und von der Bindungsenergie E B oder<br />
Ionisationsenergie der Elektronen im Targetmaterial ab. Bethe, Bloch, Lindhard,<br />
Scharf und Schiøt haben die genaue quantenmechanische Rechnung durchgeführt,<br />
Physik IV - V4, Seite 3
das Resultat gilt auch für relativistische Teilchen:<br />
dE<br />
dx = − Z2 1e 4 n e<br />
4π ·ε 2 0 v2 m e<br />
·<br />
[<br />
ln<br />
( 2me v 2 ] )−ln(1−β 2 )−β 2 , wo β = v/c.<br />
〈E B 〉<br />
Dieser Ausdruck heißt oft Bethe-Bloch-Formel. Für β ≪ 1 und b max /b min =<br />
(2m e v 2 )/〈E B 〉 stimmt unser Ausdruck <strong>mit</strong> diesem überein.<br />
dE/dx [MeV/cm]<br />
0.1<br />
0.01<br />
0.001<br />
minimal ionisierend<br />
0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000<br />
Energie [MeV]<br />
Der Energieverlust von Protonen in Luft<br />
ist links dargestellt. Zunächst sinkt der<br />
Energieverlust <strong>mit</strong> zunehmender Energie,<br />
erreicht ein flaches Minimum und beginnt<br />
dann langsam (ungefähr logarithmisch) wieder<br />
zu steigen. Im Gebiet des minimalen<br />
Energieverlustes heißen Projektile minimal<br />
ionisierend. Dazu müssen sie eine kinetische<br />
Physik IV - V4, Seite 4
Energie von etwa der doppelten Ruheenergie haben.<br />
Oft ist es einfacher, die Elektronendichte im Targetmaterial durch die Dichte ρ<br />
selber auszudrücken. Dazu verwenden wir<br />
n e = Z t·n a ≈ Z t<br />
A·m p<br />
·ρ ≈ (0.4−0.5)·<br />
ρ<br />
m p<br />
,<br />
wo n a die Dichte der Atome im Target und m p die Protonenmasse ist. Wir haben<br />
dann<br />
dE<br />
ρ·( ) 2 Z1·e<br />
dx ∝ ∝ ρ Z2 1<br />
.<br />
v E kin<br />
Deshalb schreibt man oft das Bremsvermögen von <strong>Materie</strong> in Einheiten<br />
eV/(g/cm 2 ). (1/ρ)·(dE/dx) hängt nur noch schwach von der Target-Substanz<br />
ab.<br />
Physik IV - V4, Seite 5
Stopping Power [MeV/(g/cm 2 )]<br />
10000<br />
1000<br />
100<br />
10<br />
Lead<br />
Air<br />
1<br />
0.001 0.01 0.1 1 10 100 1000<br />
Energy [MeV]<br />
DieentscheidendeRollespieltdieIonisationsenergie<br />
(bzw.die <strong>mit</strong>tlere Bindungsenergie) der<br />
Targeteletronen. Ist sie größer, verkleinert sich<br />
(1/ρ) · (dE/dx) und es braucht etwas mehr<br />
“Gramm pro Quadratzentimeter” um gegen<br />
<strong>Strahlung</strong> abzuschirmen. Im Beispiel nebenan<br />
ist die sog.stopping power, wie der spezifische<br />
Energieverlust englisch heißt, für Luft und Blei<br />
gezeigt. Wegen der größeren Bindungsenergie<br />
E B in Blei ist der spezifische Energieverlust von Blei bei gleicher Kolonnendichte<br />
(g/cm 2 oder kg/m 2 )) etwas kleiner als der von Luft. Natürlich schirmt ein<br />
Zentimeter Blei besser ab, als ein Zentimeter Luft, aber eben nicht ein g/cm 2 .<br />
Tabellen von spezifischen Energieverlusten können am NIST berechnet werden:<br />
http://physics.nist.gov/PhysRefData/Star/Text/intro.html<br />
Physik IV - V4, Seite 6
Der Bragg-Peak<br />
Energiedeposition [MeV/cm]<br />
4<br />
3.5<br />
3<br />
2.5<br />
2<br />
1.5<br />
1<br />
0.5<br />
0<br />
0 0.5 1 1.5 2 2.5 3 3.5 4<br />
Strecke in Luft bei Normdruck [cm]<br />
Weil ein Projektil bei kleineren Energien mehr<br />
Energie verliert, als bei größeren, bedeutet<br />
dies, dass es beim Durchgang durch <strong>Materie</strong><br />
gegen das Ende seiner Bahn besonders viel<br />
Energie verliert. Links ist dieser Sachverhalt<br />
für ein 5 MeV α-Teilchen in Luft bei<br />
Normdruck dargestellt. Die Reichweite beträgt<br />
offensichtlichetwadreiZentimeter,gegenEnde<br />
seiner Bahn deponiert das α-Teilchen fast 3.5<br />
mal soviel Energie pro cm als am Anfang.<br />
Dieser Peak am Ende der Bahn heißt Bragg- Peak und wird z.B.in der<br />
Strahlentherapie gegen Krebs zielgerichtet eingesetzt. Die Kurve links wurde<br />
<strong>mit</strong> der Bethe-Bloch-Formel berechnet.<br />
Physik IV - V4, Seite 7
N(x)/N 0<br />
Reichweite <strong>ionisierender</strong> <strong>Strahlung</strong><br />
E 2 > E 1<br />
Die <strong>mit</strong>tlere Reichweite 〈R〉 von Teilchen<br />
wird aus ihrer Anfangsenergie E 0 und ihrem<br />
<strong>mit</strong>tleren Energieverlust pro Längeneinheit<br />
berechnet,<br />
E 1<br />
〈R 1 〉 〈R 2 〉<br />
〈R〉 = −<br />
∫ 0<br />
E 0<br />
dE<br />
dE/dx .<br />
x<br />
Die <strong>mit</strong>tlere Reichweite ist ist links dargestellt.<br />
Weil der jeweilige Energieverlust eines<br />
Teilchens statistisch streut, wird die Reichweite<br />
an jener Stelle definiert, bis zu der die Hälfte aller Teilchen in das Material<br />
eindringen. Die Reichweite ist natürlich sowohl vom Material, wie auch von<br />
Teilchensorte und -energie abhängig.<br />
Physik IV - V4, Seite 8
Range [g/cm 2 ]<br />
10000<br />
1000<br />
100<br />
10<br />
1<br />
0.1<br />
0.01<br />
0.001<br />
0.0001<br />
1e−05<br />
electrons<br />
α-particles<br />
protons<br />
1e−06<br />
0.001 0.01 0.1 1 10 100 1000 10000<br />
Energy [MeV]<br />
Die Energieabhängigkeit der Reichweiten von<br />
Elektronen, Protonen und α-Teilchen ist<br />
nebenan dargestellt. Offensichtlich muss bei<br />
Elektronen noch ein weiterer Prozess eine Rolle<br />
spielen. In der Tat müssen bei relativistischen<br />
Elektronen (E > m e c 2 ) <strong>Strahlung</strong>sverluste<br />
berücksichtigt werden. Die Streuung der<br />
Elektronen an anderen Elektronen führt zu<br />
einer Beschleunigung und die beschleunigten<br />
Ladungen strahlen (Bremsstrahlung). Dies<br />
führt zu einer langsameren Zunahme der Reichweite <strong>mit</strong> steigender Energie.<br />
<strong>Strahlung</strong>sverluste spielen auch bei anderen Teilchen eine Rolle, aber eben nicht<br />
imhierabgebildetenEnergiebereich.FürProtonenkannderAnsatzerahntwerden.<br />
Physik IV - V4, Seite 9
Stopping Power [MeV/(g/cm 2 )]<br />
100<br />
10<br />
1<br />
0.1<br />
0.01<br />
Spezifischer Energieverlust<br />
von Elektronen in Luft<br />
Energieverlust von Elektronen<br />
Total<br />
<strong>Strahlung</strong>s−<br />
korrektur<br />
Bethe−<br />
Bloch<br />
0.001<br />
0.01 0.1 1 10 100 1000<br />
Energy [MeV]<br />
Die beiden Komponenten des Energieverlustes<br />
von Elektronen sind links für Luft dargestellt.<br />
Man sieht, dass die <strong>Strahlung</strong>skorrektur etwa<br />
bei E ≈ m e c 2 einsetzt aber erst bei einem<br />
Mehrfachen dieser Energie zu dominieren<br />
beginnt.<br />
Weil energiereiche Elektronen <strong>mit</strong> den<br />
gleich schweren Elektronen im Medium<br />
wechselwirken, können sie diesen im Maximum<br />
ihre ganze kinetische Energie abgeben.<br />
Elektronen streuen deshalb wesentlich mehr als schwere Projektile, ein einfallender<br />
paralleler Elektronenstrahl wird daher viel schneller diffus und seine Reichweite ist<br />
weniger klar definiert als die schwerer Projektile.<br />
Physik IV - V4, Seite 10
<strong>Wechselwirkung</strong> von γ-<strong>Strahlung</strong> <strong>mit</strong> <strong>Materie</strong><br />
γ-<strong>Strahlung</strong> ist elektrisch neutral und trotzdem ionisierend. Sie kann nicht über<br />
Coulomb-Kräfte wechselwirken sondern tut dies via<br />
elastische Streuung (sog.Rayleigh-, resonante oder Thompson-Streuung)<br />
inelastische Streuung (sog.Compton-Streuung)<br />
Absorption in einer Elektronenhülle (sog.Photoeffekt)<br />
Absorption in einem Atomkern (sog.Kern-Photoeffekt)<br />
Paarbildung (in der Teilchenpaare erzeugt werden)<br />
Physik IV - V4, Seite 11
Photonen können also über verschiedene Prozesse <strong>mit</strong> <strong>Materie</strong> wechselwirken,<br />
deren Bedeutung sich <strong>mit</strong> der Energie der Photonen allerdings stark ändert. Wir<br />
diskutieren die Prozesse nun <strong>mit</strong> aufsteigender Energie.<br />
Wirkungsquerschnitte für die einzelnen Prozesse können am US-National<br />
Institute of Standards and Technology (NIST) gefunden werden. Das<br />
Programm XCOM beinhaltet die neusten Messungen von Wirkungsquerschnitten.<br />
http://physics.nist.gov/PhysRefData/Xcom/Text/XCOM.html<br />
Physik IV - V4, Seite 12
Die Thomson-Streuung<br />
Als einfachsten Fall untersuchen wir<br />
die Streuung von Licht an freien<br />
Elektronen. Die Abbildung links zeigt<br />
eine Kompositaufnahme der solaren<br />
Korona, in der freie Elektronen das Licht<br />
von der Photosphäre zum Beobachter<br />
hinstreuen.DerProzessheißtThomson-<br />
Streuung und ergibt sich für Frequenzen<br />
ω ≫ ω 0 , wo ω 0 die Resonanzfrequenz<br />
eines freien Elektrons sei. Wenn wir<br />
Licht als ebene Welle ansetzen, ⃗ E(t) = ⃗ E0 · exp(−iωt), und auf ein Elektron<br />
die entsprechende Kraft ⃗ F = q · ⃗ E wirken lassen, so können wir seine<br />
Bewegungsgleichung durch die eines harmonischen Oszillators nähern. Das<br />
Elektron wird dabei zu kohärenten Schwingungen angeregt und strahlt dabei<br />
Physik IV - V4, Seite 13
ab (Dipolstrahlung).<br />
Physik IV - V4, Seite 14
Die Rayleigh-Streuung<br />
σ blau<br />
σ rot<br />
=<br />
Rayleigh-Streuung tritt immer dann auf,<br />
wenn die streuenden Partikel kleiner sind<br />
als die Wellenlänge des gestreuten Lichtes.<br />
Der Streuquerschnitt ist dann proportional<br />
zu ω 4 . Prominentestes Beispiel der Rayleigh-<br />
Streuung ist der blaue Himmel. Wegen der<br />
Frequenzabhängigkeit ist die Intensität des<br />
gestreuten blauen Lichtes höher als die des<br />
roten Lichtes,<br />
(<br />
ωblau<br />
ω rot<br />
) 4<br />
=<br />
(<br />
λrot<br />
λ blau<br />
) 4<br />
≈ 16,<br />
Blaues Licht wird etwa 16 mal stärker gestreut wird, als rotes. Das Bild stammt<br />
Physik IV - V4, Seite 15
von Wikipedia.<br />
Physik IV - V4, Seite 16
Herleitung der Abhängigkeit von σ ∝ 1/λ 4<br />
Lord Rayleigh (J.W.Strutt, Philos.Mag., 41, 107, 274<br />
Es<br />
(1871)) hat für den Streuquerschnitt im langwelligen<br />
⃗E i<br />
BereicheineeleganteHerleitung<strong>mit</strong>telsDimensionsanalyse<br />
gefunden. Ist ein streuendes Partikel wesentlich kleiner,<br />
r ≪ λ als die Wellenlänge des Lichtes, so oszillieren dessen<br />
Komponenten alle in Phase <strong>mit</strong> dem äußeren Feld E i .<br />
Deshalb ist das gestreute Feld, E s proportional zum<br />
Volumen V des Partikels und zum äußeren Feld.<br />
Wegen Energieerhaltung gilt auch Es 2 ∝ 1/r 2 . Aus Dimensionsgründen muss<br />
dann gelten: E s ∝ E iV<br />
rλ 2 , weil nur noch das Quadrat der Wellenlänge λ die richtige<br />
Einheit hat, um die Proportionalität zu gewährleisten. Deshalb gilt<br />
E 2 s ∝ E2 i V 2<br />
r 2 λ 4 , also σ ∝ λ−4 ∝ ω 4 .<br />
Physik IV - V4, Seite 17
Nucleus<br />
gamma ray<br />
orbital<br />
electron<br />
photo electron<br />
from K−shell<br />
Der Photo-Effekt<br />
Nucleus<br />
K α<br />
X−ray<br />
Bei Photoeffekt wird ein γ-Quant<br />
durch ein Hüllenelektron absorbiert,<br />
welches seinen Ort wiederum <strong>mit</strong><br />
einer Energie<br />
E kin = h·ν −E B<br />
verlässt. Das absorbierende Atom<br />
oderIon(dasabsorbierendeMaterial)<br />
erfährt wegen der Absorption des γ-Quants einen Rückstoß (Das γ-Quant ist ja<br />
dann verschwunden!). Der Wirkungsquerschnitt für den Photoeffekt ist<br />
σ ph ∼ σ 0·Z 5·<br />
(<br />
me c 2<br />
E γ<br />
) 7/2<br />
,<br />
Physik IV - V4, Seite 18
wo σ 0 = (8/3)π · r 2 e der Thomson-Streuquerschnitt und r e = e2/(8πε 0 m e c 2 )<br />
der klassische Elektronenradius ist. Deshalb ist für schwere Elemente (Z 5 !) der<br />
Photoeffekt für E γ < E B der überwiegende Absorptionsmechanismus.<br />
Physik IV - V4, Seite 19
Der Compton-Effekt<br />
Photon, E 0 , p 0 , λ 0<br />
⃗p 0 = ¯h ⃗ k 0 Elektron<br />
Photon<br />
E 1 , p 1 , λ 1<br />
⃗p 1 = ¯h ⃗ k 1<br />
φ<br />
θ<br />
⃗p e<br />
In P4 V1 haben wir bereit die<br />
Comptonsche Streuformel ergeleitet,<br />
λ 1 −λ 0 = λ c (1−cosφ), (1)<br />
wo λ c = h/(m e c) die Compton-<br />
Wellenlänge ist. Anmultiplizieren von<br />
1/λ 0 = ν 0 /c liefert<br />
λ c<br />
λ 0<br />
= hν 0<br />
m e c 2.<br />
Die Compton-Wellenlänge ist der Quotient aus Photonenenergie und Ruheenergie<br />
des Streuers.<br />
Physik IV - V4, Seite 20
Der Wirkungsquerschnitt für die Compton-Streuung wurde 1929 von O.Klein und<br />
Y.Nishina berechnet, für E γ ≫ m e c 2 gilt<br />
σ c = πre 2 ·Z m ec 2 [ ( )] 1<br />
E γ 2 + ln 2Eγ<br />
m e c 2 .<br />
Die Comptonsche Streuformel kann auch geschrieben werden als<br />
1<br />
E 1<br />
− 1 E 0<br />
=<br />
E 1 =<br />
1<br />
m e c2(1−cosφ), bzw.<br />
E 0<br />
.<br />
1+ E 0(1−cosφ)<br />
m e c 2<br />
Physik IV - V4, Seite 21
counts per bin<br />
Compton-Spektrum<br />
Compton-Kante<br />
Photopeak<br />
Energie<br />
Weil das gestreute Elektron rasch seine Energie<br />
an das umliegende Medium abgibt, ist die durch<br />
Compton-Streuung an das Medium übertragene<br />
Energie<br />
⎛ ⎞<br />
1<br />
∆E = E 0 −E 1 = E 0·<br />
⎝1 −<br />
1+ E 0(1−cosφ)<br />
m e c 2<br />
Der maximale Energieübertrag ergibt sich für φ = π, also eine Streuung um 180<br />
Grad. Einsetzen ergibt<br />
2E0<br />
2 ∆E max =<br />
m e c 2 .<br />
+2E 0<br />
Das bedeutet, dass ein Detektor, in dem γ-Quanten via Compton-Effekt<br />
gemessen werden, bei dieser höchsten Energie eine “Kante” aufweisen wird,<br />
die sog.Compton-Kante.<br />
⎠.<br />
Physik IV - V4, Seite 22
Die Paarbildung<br />
Bei der Paarproduktion wird<br />
im starken Feld der Atomhülle<br />
oder des Kerns ein Elektronen-<br />
Positronen-Paar erzeugt. Das<br />
0.511 MeV Positron annihiliert rasch <strong>mit</strong><br />
1.2 MeV<br />
gamma ray<br />
gamma ray<br />
einem umgebenden Elektron unter<br />
Nucleus<br />
Aussendung von zwei Photonen<br />
der Energie E γ ≥ 511 keV. Das<br />
Elektron verliert seine Energie nach<br />
Bethe-Bloch, die entstandenen<br />
0.511 MeV<br />
gamma ray<br />
γ-Quanten verlieren sie durch<br />
Compton-Streuung (für die leichten Elemente) oder über den Photoeffekt.<br />
positron<br />
electron<br />
Physik IV - V4, Seite 23
Zusammenfassung<br />
σ [cm 2 /g]<br />
10000<br />
100<br />
1<br />
0.01<br />
0.0001<br />
1e−06<br />
1e−08<br />
1e−10<br />
1e−12<br />
Photoeffekt<br />
Compton-Effekt<br />
Nukleare Paarproduktion<br />
1e−14<br />
0.001 0.01 0.1 1 10 100 1000 10000100000<br />
Eγ [MeV]<br />
Effekt an Prominenz gewinnen.<br />
Der gesamte Wirkungsquerschnitt für γ-<br />
Quanten setzt sich also aus den verschiedenen<br />
eingangs genannten Prozessen zusammen.<br />
Diese sind sowohl von der Energie des<br />
Projektils wie auch von der Kernladungszahl<br />
des Targets abhängig. Links ist der totale<br />
Wirkungsquerschnitt für Blei dargestellt, einige<br />
behandelteProzessesindfarbighervorgehoben.<br />
Für ein leichteres Element wird der Compton-<br />
Physik IV - V4, Seite 24
Abschirmung/Schwächungskoeffizienten<br />
Beim Durchgang durch <strong>Materie</strong> werden<br />
Absorber<br />
Röntgen- oder γ-strahlen gestreut. In der<br />
I 0 I links skizzierten Konfiguration sind die<br />
gestreuten Photonen rot und gestrichelt<br />
Quelle Detektor dargestellt, die trans<strong>mit</strong>tierten schwarz. Beim<br />
Detektor kommen nicht alle ausgesandten<br />
Photonen an. Die Schwächung des Strahls ist proportional zur Intensität des<br />
Strahls,<br />
dI<br />
dx = −µI und da<strong>mit</strong> I(x) = I 0·exp(−µ·x) im Medium.<br />
Die Proportionalitätskonstante µ heißt Schwächungskoeffizient. Weil die<br />
Abschirmung auch proportional zur Dichte des Materials ist, ist es sinnvoll, den<br />
sog.Massenschwächungskoeffizienten µ/ρ einzuführen.<br />
Physik IV - V4, Seite 25
µ/ρ [cm 2 /g]<br />
10000<br />
1000<br />
100<br />
10<br />
1<br />
Abschirmung/Schwächungskoeffizienten<br />
Pb<br />
Die γ-<strong>Strahlung</strong> wird durch <strong>Materie</strong><br />
abgeschirmt. Die Abschirmung läßt<br />
sichdurchdensog.Massenschwächungskoeffizienten<br />
(µ/ρ) i<br />
beschreiben.<br />
Die Massenschwächungskoeffizienten (µ/ρ) i<br />
der Elemente können im Netz gefunden<br />
werden 1 .<br />
0.1<br />
0.01<br />
0.001 0.01 0.1 1 10<br />
Eγ [MeV]<br />
Die Massenschwächungskoeffizienten für<br />
zusammengesetzte Materialien µ/ρ ¯<br />
∑<br />
=<br />
wi (µ/ρ) i<br />
können aus der prozentualen<br />
Gewichtsverteilung der Elemente berechnet oder im Netz gefunden werden 2 .<br />
1 http://physics.nist.gov/PhysRefData/XrayMassCoef/tab3.html<br />
2 http://physics.nist.gov/PhysRefData/XrayMassCoef/tab4.html<br />
Physik IV - V4, Seite 26
E n , ⃗p n<br />
n<br />
E ′ n , ⃗p′ n<br />
E ′ p , ⃗p p′<br />
<strong>Wechselwirkung</strong> von Neutronen <strong>mit</strong> <strong>Materie</strong><br />
p<br />
E p , ⃗p p<br />
∑ ⃗pi = ∑ ⃗p ′ i<br />
Neutronen sind ungeladene Teilchen und können<br />
elektromagnetisch <strong>mit</strong> den Elektronen im Medium<br />
höchstens über ihr magnetisches Moment<br />
wechselwirken. Viel stärker ist aber ihre<br />
<strong>Wechselwirkung</strong> <strong>mit</strong> den Atomkernen, die man für<br />
niedrige Energien oft durch elastische Stöße harter<br />
Kugeln nähern kann. Dabei gelten sowohl Energiewie<br />
auch Impulserhaltung. Treten Kernreaktionen auf,<br />
so müssen die Stöße inelastisch behandelt werden.<br />
⃗p n +⃗p K = ⃗p ′ n+⃗p ′ K,<br />
p 2 n<br />
2m n<br />
+ p2 K<br />
2m K<br />
= p′2 n<br />
2m n<br />
+ p′2 K<br />
2m K<br />
+Q.<br />
Physik IV - V4, Seite 27
Elastische Stöße im Schwerpunktsystem II<br />
Oft wird der eine Stoßpartner vor dem Stoß in Ruhe sein, etwa wenn ein Teilchen<br />
der Masse m 1 in einem Beschleuniger auf ein Targetteilchen der Masse m 2 trifft.<br />
Dann gilt also ⃗v 2 =⃗0. Wir wollen diesen wichtigen Spezialfall untersuchen. Der<br />
Einfachheit halber berücksichtigen wir nur elastische Stöße und untersuchen, wie<br />
der Streuwinkel θ die Streuresultate beeinflusst.<br />
Die Schwerpunktgeschwindigkeit ist<br />
⃗v S = ⃗u S = m 1⃗v 1 +m 2<br />
⃗0<br />
m 1 +m 2<br />
= ⃗v 1<br />
1+X , wo X = m 2<br />
m 1<br />
.<br />
Wir rechnen in das Schwerpunktsystem um:<br />
⃗v 1,S = ⃗v 1 −⃗v S = X<br />
1+X ⃗v 1,<br />
Physik IV - V4, Seite 28
⃗v 2,S = ⃗v 2 −⃗v S = − ⃗v 1<br />
1+X<br />
⃗u 1,S = ⃗u 1 −⃗v S<br />
Wir lösen die letzte Gleichung nach ⃗u 1 auf und quadrieren das Resultat.<br />
u 2 1 = u 2 1,S +<br />
v 2 1<br />
v 1<br />
(1+X) 2 +2u 1,S<br />
1+X cosθ<br />
Das Resultat bringen wir auf einen Nenner<br />
u 2 1 = (1+X)2 u 2 1,S +v2 1 +2(1+X)u 1,S v 1 cosθ<br />
(1+X) 2 .<br />
Wegen der Energieerhaltung im Schwerpunktsystem für elastische Stöße<br />
p ′2<br />
1,S /(2µ) = p2 1,S /(2µ) gilt auch (sofern m 1 und m 2 gleich bleiben!) u 2 1,S = v2 1,S<br />
Physik IV - V4, Seite 29
und <strong>mit</strong> v 1,S = v 1 X/(1+X) gilt folglich<br />
u 2 1 = v1<br />
2 X 2 +2Xcosθ +1<br />
(1+X) 2 .<br />
Energieübertrag in einem elastischen Stoß:<br />
∆E kin<br />
E kin<br />
= E′ kin,1 −E kin,1<br />
E kin,1<br />
= X2 +2Xcosθ +1<br />
(1+X) 2 −1.<br />
Die drei folgenden Bilder zeigen den maximalen Energieübertrag, eine Rose im<br />
Bleicontainer im Neutronenlicht der GKSS und eine Röntgenaufnahme (links)<br />
und eine Neutronenradiographie (rechts) eines Wasserhahns (GKSS).<br />
Physik IV - V4, Seite 30
1<br />
θ = π<br />
θ = 3/4 π<br />
|∆E kin<br />
/ E kin<br />
|<br />
0,1<br />
Physik IV - V4, Seite 31<br />
0,01<br />
0,01 0,1 1 10 100<br />
m 2<br />
/m 1
Physik IV - V4, Seite 32
Physik IV - V4, Seite 33
Biologische Effekte von <strong>Strahlung</strong><br />
Passiert ionisierende <strong>Strahlung</strong> durch Gewebe, so können dabei molekulare<br />
Bindungen zerstört oder Atome ionisiert werden. Beim Knacken von Wasser<br />
(H 2 O) entstehen freie Radikale. Wesentlich schädlicher sind aber Strahlenschäden<br />
in der DNS im Erbgut. Dabei unterscheidet man nach ICRP (International<br />
Commission on Radiological Protection):<br />
Deterministische Strahlenwirkungen sind solche Wirkungen, bei<br />
denen der Schweregrad des Strahlenschadens eine Funktion<br />
der Dosis ist. Bei vielen deterministiscn Wirkungen besteht<br />
eine Dosisschwelle, unterhalb derer keine klinischen Symptome<br />
auftreten.<br />
Stochastische Strahlenwirkungen sind solchem bei denen die<br />
Eintrittswahrscheinlichkeit für einen Strahleneffekt, nicht<br />
aber dessen Schweregrad von der Energiedosis abhängt.<br />
Physik IV - V4, Seite 34
1<br />
0.5<br />
W’keit<br />
D S<br />
D 50<br />
D max<br />
Dosis<br />
BeispielefürdeterministischeStrahlenschäden<br />
sind Strahlenkrankheit, Strahlentod,<br />
Absterben von Gewebe bei lokaler<br />
Wirkung. Dieses wird bei der<br />
Tumorbekämpfung gezielt ausgenutzt.<br />
Dabei wird die Abhängigkeit von der<br />
Dosisschwelle ausgenutzt.<br />
BeispielefürstochastischeStrahlenschäden<br />
sind Tumor oder vererbbare Schäden. Stochastischen Schäden wird keine<br />
Dosisschwelle unterstellt (Linear Non-Threshold-Model), was aber durch neuere<br />
Forschung nicht gestützt wird.<br />
Physik IV - V4, Seite 35
Wiederholung: Einheiten der Aktivität<br />
Heute wird Aktivität in Einheiten von Becquerel gemessen,<br />
1Becquerel = 1Bq = 1Zerfall pro Sekunde.<br />
Die Wirkung radioaktiver <strong>Strahlung</strong> wird in zwei (drei) Einheiten gemessen.<br />
Die Ionisation wird gemessen in Röntgen, wobei ein Röntgen diejenige<br />
<strong>Strahlung</strong>smenge an γ-<strong>Strahlung</strong> ist, die 2 · 10 9 Ionenpaare pro Mililiter<br />
Luft erzeugt, oder, in anderen Worten,<br />
1Röntgen = 1R = 2.58·10 −4C kg (Luft).<br />
Oft ist die abgegebene Energiemenge pro Masse, die sog.Dosis, interessanter, sie<br />
Physik IV - V4, Seite 36
wird in Gray gemessen,<br />
1Gray = 1Gy = 1 J<br />
kg .<br />
Ist die biologische Wirksamkeit gefragt, wird die Dosis <strong>mit</strong> einem Qualitätsfaktor<br />
Q multipliziert, die sog.Äquivaläntdosis wird in Sievert gemessen,<br />
1Sievert = 1Sv = Q·Gy.<br />
DieQualitätsfaktorenwerdendurchdie“InternationalCommissiononRadiological<br />
Protection” (ICRP) definiert. Mehr dazu später in dieser Vorlesung.<br />
Überlegung: Was ist 1 J/kg?<br />
Um wieviel erwärmt sich 1 kg Wasser bei einer Energiezufuhr von 1J?<br />
Die Wärmemenge = ∆T m c H2 O ist also 1 J, die Masse m = 1kg und folglich<br />
∆T = 1/c H2 O in Einheiten von J, K, kg. Mit c H2 O = 4.1813 · 10 3 J/kg/K ist<br />
∆T = 1/4.1813·10 3 = 0.24·10 −3 K. Das ist sehr klein, aber...<br />
Physik IV - V4, Seite 37
Auswirkungen auf den Menschen<br />
Dosis Auswirkungen<br />
(Ganzkörper)<br />
< 0.25 Sv keine klinisch nachweisbaren Schäden<br />
0.25 Sv Abnahme von weißen Blutkörpern<br />
0.5 Sv Zunehmende Zerstörung von Leukozyten-bildenden Organen,<br />
was zu einer Abnahme der Infektionsresistenz führt<br />
1 Sv Deutliche Veränderungen im Blutbild, besonders Abnahme der<br />
Leukozyten und Neutrophilen (“Fresszellen”).<br />
2 Sv Übelkeit und andere Symptome<br />
5 Sv Schäden am Gastrointestinaltrakt, die zu Blutungen führen.<br />
Etwa 50%-ige Todeswahrscheinlichkeit<br />
10 Sv Zerstörung des neurologischen Systems und etwa 100%-ige<br />
Todeswahrscheinlichkeit innerhalb von 24 Stunden.<br />
Physik IV - V4, Seite 38
Maximum Permissable Dose (MPD)<br />
DieICRPundderNCRPhabendiefolgendenWertefürdiemaximalzuläßigeDosis<br />
(Maximum permissable Dose (MPD)) für Bevölkerung und beruflich exponierte<br />
Personen herausgegeben. Dabei gilt für alle Expositionen das ALARA-Prinzip<br />
(As Low As Reasonably Achievable).<br />
NCRP ICRP<br />
Bevölkerung Jährliche MPD 1 mSv 1 mSv<br />
beruflich Jährliche MPD 50 mSv 20 mSv<br />
strahlenexponierte kumulative MPD 10 mSv × Alter -<br />
Personen Schwangerschaft 5 mSv 2 mSv<br />
Zum Vergleich: Wegen der Höhenstrahlung trägt ein Langstreckenflug in 10km<br />
Höhe 6 µSv/h zur Dosis bei. Kabinenpersonal bleibt ca. 1000 Stunden in dieser<br />
Höhe, erfährt also etwa 6 mSv/a und muss als beruflich strahlenexponiertes<br />
Personal eingestuft werden.<br />
Physik IV - V4, Seite 39
Art der Strahlenquelle<br />
Natürliche Strahlenquellen<br />
Kosmische <strong>Strahlung</strong> (auf Meeresniveau)<br />
Terrestrische <strong>Strahlung</strong><br />
Äußerliche Bestrahlung<br />
Einatmen von Radon<br />
sonstige innere <strong>Strahlung</strong><br />
Summe natürliche Strahlenquellen<br />
Künstliche Strahlenquellen<br />
Medizinische Anwendungen<br />
Kernkraftwerke (Normalbetrieb)<br />
Folgen des Tschernobyl-Unfalls<br />
Atombombenversuche<br />
Sonstige künstliche <strong>Strahlung</strong><br />
Summe künstliche Strahlenquellen<br />
Summe nat. u. künstl. Strahlenquellen<br />
Effektive Dosis im Jahr<br />
0,3 mSv<br />
0.4mSv<br />
1.1 mSv<br />
0.3 mSv<br />
∼ 2 mSv<br />
1,9 mSv<br />
< 0,01 mSv<br />
< 0,016 mSv<br />
< 0,01 mSv<br />
< 0,02 mSv<br />
∼ 2 mSv<br />
∼4 mSv<br />
Physik IV - V4, Seite 40