Dynamische Systeme

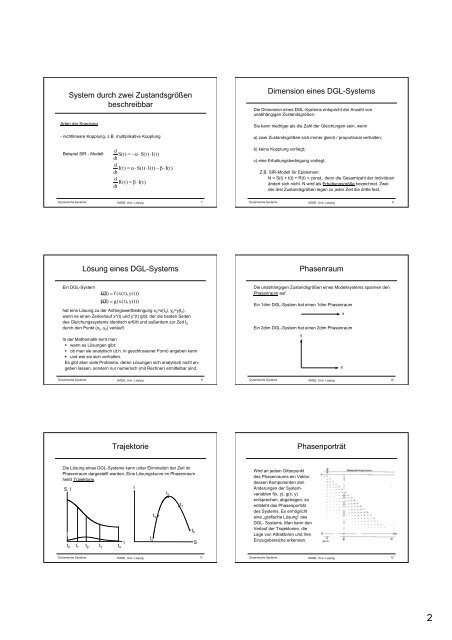
System durch zwei Zustandsgrößen
beschreibbar
Arten der Kopplung
- nichtlineare Kopplung, z.B. multiplikative Kopplung
Dimension eines DGL-Systems
Die Dimension eines DGL-Systems entspricht der Anzahl von
unabhängigen Zustandsgrößen.
Sie kann niedriger als die Zahl der Gleichungen sein, wenn
a) zwei Zustandsgrößen sich immer gleich / proportional verhalten;
Beispiel SIR - Modell:
d
S(t) = −α ⋅S(t)
⋅ I(t)
dt
d
I(t) = α ⋅S(t)
⋅ I(t) − β ⋅ I(t)
dt
d
R(t) = β⋅ I(t)
dt
b) keine Kopplung vorliegt;
c) eine Erhaltungsbedingung vorliegt.
Z.B. SIR-Modell für Epidemien:
N = S(t) + I(t) + R(t) = const., denn die Gesamtzahl der Individuen
ändert sich nicht. N wird als Erhaltungsgröße bezeichnet. Zwei
der drei Zustandsgrößen legen zu jeder Zeit die dritte fest.
Dynamische Systeme IMISE, Univ. Leipzig 7
Dynamische Systeme IMISE, Univ. Leipzig 8
Lösung eines DGL-Systems
Phasenraum
Ein DGL-System
x(t) = f (x(t),y(t))
y(t) = g(x(t),y(t))
hat eine Lösung zu der Anfangswertbedingung x 0 =x(t 0 ), y 0 =y(t 0 ),
wenn es einen Zeitverlauf x*(t) und y*(t) gibt, der die beiden Seiten
des Gleichungssystems identisch erfüllt und außerdem zur Zeit t 0
durch den Punkt (x 0 , y 0 ) verläuft.
In der Mathematik lernt man
• wann es Lösungen gibt;
• ob man sie analytisch (d.h. in geschlossener Form) angeben kann
• und wie sie sich verhalten.
Es gibt aber viele Probleme, deren Lösungen sich analytisch nicht angeben
lassen, sondern nur numerisch (mit Rechner) ermittelbar sind.
Die unabhängigen Zustandsgrößen eines Modellsystems spannen den
Phasenraum auf.
Ein 1dim DGL-System hat einen 1dim Phasenraum
Ein 2dim DGL-System hat einen 2dim Phasenraum
y
x
x
Dynamische Systeme IMISE, Univ. Leipzig 9
Dynamische Systeme IMISE, Univ. Leipzig 10
Trajektorie
Phasenporträt
Die Lösung eines DGL-Systems kann unter Elimination der Zeit im
Phasenraum dargestellt werden. Eine Lösungskurve im Phasenraum
heißt Trajektorie.
S, I
• t
50
5
0
•
0
t
S
t 0 t 1 t 3 t 0
4
t 2
I
t 3 •
t 2
•
• t 1
Wird an jedem Gitterpunkt
des Phasenraums ein Vektor,
dessen Komponenten den
Änderungen der Systemvariablen
f(x, y), g(x, y)
entsprechen, abgetragen, so
entsteht das Phasenporträt
des Systems. Es ermöglicht
eine „grafische Lösung“ des
DGL- Systems. Man kann den
Verlauf der Trajektorien, die
Lage von Attraktoren und ihre
Einzugsbereiche erkennen.
t 4
Dynamische Systeme IMISE, Univ. Leipzig 12
Dynamische Systeme IMISE, Univ. Leipzig 11
2