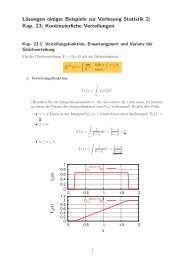
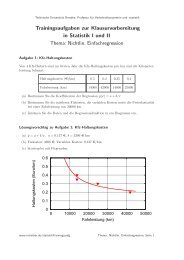
Klausur zur Vorlesung Statistik I und II, WS 2005/2006

Name: Vorname: Matrikel-Nr.:
Blatt: 1 von 5
Klausur zur Vorlesung Statistik I und II,
WS 2005/2006
Aufgabe 1
(50 Punkte)
Folgende Tabelle gibt die Zahl der Fluggäste sowie den Umfang der Luftfracht auf deutschen
Flughäfen im Jahre 2003 an:
Flughafen
Fluggäste
(in 1000)
Luftfracht
(t)
Stuttgart 3 715 10 086
München 11 990 76 993
Berlin-Tegel 5 530 6 021
Hamburg 4 700 12 351
Frankfurt/Main 23 980 783 777
Düsseldorf 7 061 23 872
Köln/Bonn 3 841 262 269
Frankfurt Hahn 1 173 18 446
10 weitere Verkehrsflugplätze 7 100 24 500
Alle restlichen 532 Flugplätze 2 513 27
(a) Geben Sie die Herfindahl-Indices der Konzentration der Fluggäste und der Luftfracht auf
die deutschen Flughäfen an. Was würde sich ändern, wenn man die 532 kleineren Flugplätze
nicht berücksichtigte
(b) Zeichnen Sie die Lorentzkurve und berechnen Sie den Gini-Koeffizienten der Konzentration
der Fluggäste auf die 18 VerkehrsflughäfenFlughäfen, ohne die 532 kleinen zu berücksichtigen.
(c) Ändern sich die relativen Konzentrationsmaße deutlicher als die absoluten, wenn man die
kleinen Flughäfen hinzunimmt (keine Rechnung verlangt!) Was ist also das Problem der
relativen Konzentrationsmaße
(d) Geben Sie den Korrelationskoeffizienten zwischen der Zahl der Fluggäste und der Menge
an Luftfracht an.
1

Name: Vorname: Matrikel-Nr.:
Blatt: 2 von 5
Aufgabe 2
(20 Punkte)
Der Statistik Dresdner Einwohner entnimmt man für Juni 2005 folgende Daten:
zugezogene Personen 1 506
fortgezogene Personen 1 306
innerhalb Dresdens umgezogene Personen 3 706
Eheschließungen 653
Scheidungen 11
Lebendgeborene 484
Gestorbenene 387
Einwohner 481 429
(a) Geben Sie für jedes statistische Merkmal an, ob es sich um eine Bestands- oder eine
Bewegungsmasse handelt. Finden Sie ein korrespondierendes Paar von Bestands- und Bewegungsmassen.
(b) Wie hoch war die Einwohnerzahl im Mai 2005
Aufgabe 3
(50 Punkte)
Für den Fortzug von Dresden in die Alten Bundesländer ist folgende Zeitreihe gegeben:
Jahr
Quartal Q I Q II Q III Q IV
2001 1 600 1 580 2 420 1 980
2002 1 510 1 420 1 820 1 520
2003 1 370 1 200 1 640 1 390
2004 1 240 1 060 1 590 1 440
(a) Begründen Sie, warum ein multiplikatives Modell dem Datenmaterial angemessen ist
(b) Führen Sie eine multiplikative Saisonbereinigung durch. Geben Sie die Saisonindexziffern
an. Wie wäre nach diesem Modell die Prognose für die vier Quartale 2005
2

Name: Vorname: Matrikel-Nr.:
Blatt: 3 von 5
Aufgabe 4
(50 Punkte)
Der Statistikstelle der Landeshauptstadt Dresden entnimmt man folgende Verteilung der 481 429
Einwohner Dresdens auf die einzelnen 365 Geburtstage (29. Februar nicht berücksichtigt):
Dresdner Einwohner nach Geburtstagen
Durchschnitt
Feb Apr Jun Aug Okt Dez
(a) Die durchgezogene Kurve gibt eine Glättung der Daten an, welche man z.B. mit dem
gleitenden arithmetischen Mittel gewinnen kann.
(i) Wie groß muss man den Glättungsparameter des gleitenden Mittels wählen, damit
die Geburtstags-Spitze im September nahezu “weggemittelt” wird, die jahreszeitliche
Verteilung “mehr Geburtstage im Frühjahr als im Herbst” aber korrekt wiedergegeben
wird (keine Rechnung, Angabe der Größenordnung genügt!)
(ii) Was muss man zusätzlich bei der Glättung beachten (bedenken Sie, dass der Jahresbeginn
am 1. Januar willkürlich ist!)
(b) Weicht die Geburtstagsverteilung bei einer Fehlerwahrscheinlichkeit von 1 % signifikant
von einer Gleichverteilung ab Berücksichtigen Sie dabei, dass in der Grafik die Fläche
zwischen dem Mittelwert und der geglätteten Kurve von Mitte Januar bis Juli (und auch
die entsprechende Nettofläche zwischen ungeglätteten Daten und Mittelwert) etwa sechs
der von den punktierten Linien begrenzten “Kästchen” entspricht.
Hinweis: Kolmogorow-Smirnov-Anpassungstest.
(c) Kann man die Geburtstags-Spitze im September durch eine statistische Schwankung erklären,
wenn man den Kolmogorow-Smirnov-Test wie oben zugrundelegt Falls nein, hat
man damit statistisch eine besonders “fruchtbaren” Empfängniszeitraum im Dezember
bewiesen
(d) In Österreich wurden bei der Volkszählung im Jahre 2001 am ersten Januar 37 700 Geburtstage
erfasst, im Mittel jedoch nur 22 082. In Dresden gab es am 1. Januar ebenfalls
erstaunlich viele Geburtstage (linkester Datenpunkt der Grafik). Was könnte die Ursache
dieser hochsignifikanten Abweichungen sein (jede plausible Erklärung ergibt volle Punktzahl!)
3

Name: Vorname: Matrikel-Nr.:
Blatt: 4 von 5
Aufgabe 5
(30 Punkte)
Eine Kfz-Haftpflichtversicherung teilt ihre Kunden in vier Schadenfreiheitsklassen (SF-Klassen)
ein. Zur Ermittlung der “Schadenfreiheitsrabatte” wird folgende Tabelle der im letzten Jahr
eingehenden Schadensmeldungen zugrundegelegt (die “Unfallfreiheit” gilt natürlich für den Zeitraum
vor der aktuellen Schadensmeldung):
SF-Klasse
Zahl der Mitglieder
Anteil an den Schadensmeldungen
SF 1 (unfallfrei ≤ 2 Jahre) 50 000 30%
SF 2 (unfallfrei 2-5 Jahre) 80 000 30%
SF 3 (unfallfrei 5-10 Jahre) 80 000 24%
SF 4 (unfallfrei > 10 Jahre) 66 667 16%
Die Mitglieder der SF 1 zahlen 100% des Referenzbeitrages, die Mitglieder der SF k = 2 bis
4 bekommen Rabatte, so dass der zu zahlende Versicherungsbetrag proportional zur bedingten
Wahrscheinlichkeit dafür ist, dass sie im Bezugszeitraum (mindestens) eine Schadensmeldung
eingereicht haben. Bestimmen Sie die Rabatte mit Hilfe des Satzes von Bayes und berücksichtigen
Sie dabei das Gesetz der großen Zahlen.
Hinweis: zu berechnen sind also Quotienten der bedingten Wahrscheinlichkeiten einer Schadensmeldung
eines Mitglieds, falls dieses in SF k ist, bezogen auf die Schadenshäufigkeit von
Mitgliedern der SF 1.
Aufgabe 6
(40 Punkte)
Einer Befragung nach der Verkehrsmittelwahl in Dresden ergab 2002 für den Arbeitsweg folgende
Ergebnisse: 43% PKW Fahrer, 3% PKW Mitfahrer, 1 % Motorrad, Moped o. ä., 20%
Straßenbahn, 12% Bus, 3% S-Bahn, 13% Fahrrad und nur 5% zu Fuß ohne Benutzung anderer
Verkehrsmittel.
(a) Zeichnen Sie ein Tortendiagramm dieses Sachverhalts.
(b) Der Stichprobenfehler soll für alle Anteile bei einem Signifikanzniveau von 5% kleiner als
2% sein. Wie groß muss man den Stichprobenumfang mindestens wählen
(c) Gegenüber dem Vorjahr stieg der Anteil der Fahrradbenutzer von 11% auf 13%. Beide
Stichproben hatten den Umfang 2000. Sind die Unterschiede bei einer Fehlerwahrscheinlichkeit
von 1% signifikant Verwenden Sie den Differenztest für zwei unabhängige Stichproben!
4

Name: Vorname: Matrikel-Nr.:
Blatt: 5 von 5
Tabellen
Quantile z q der Standardnormalverteilung
q z q q z q q z q q z q
0.995 2.5758 0.945 1.5982 0.880 1.1750 0.680 0.4677
0.990 2.3263 0.940 1.5548 0.860 1.0803 0.660 0.4125
0.985 2.1701 0.935 1.5141 0.840 0.9945 0.640 0.3585
0.980 2.0537 0.930 1.4758 0.820 0.9154 0.620 0.3055
0.975 1.9600 0.925 1.4395 0.800 0.8416 0.600 0.2533
0.970 1.8808 0.920 1.4051 0.780 0.7722 0.580 0.2019
0.965 1.8119 0.915 1.3722 0.760 0.7063 0.560 0.1510
0.960 1.7507 0.910 1.3408 0.740 0.6433 0.540 0.1004
0.955 1.6954 0.905 1.3106 0.720 0.5828 0.520 0.0502
0.950 1.6448 0.900 1.2815 0.700 0.5244 0.500 0.0000
Quantile t (q)
n
der Studentschen t-Verteilung
n q = 0.60 0.70 0.80 0.90 0.95 0.975 0.990 0.995 0.999 0.9995
1 0.325 0.727 1.376 3.078 6.314 12.706 31.821 63.657 318.31 636.62
2 0.289 0.617 1.061 1.886 2.920 4.303 6.965 9.925 22.327 31.598
3 0.277 0.584 0.978 1.638 2.353 3.182 4.541 5.841 10.215 12.924
4 0.271 0.569 0.941 1.533 2.132 2.776 3.747 4.604 7.173 8.610
5 0.267 0.559 0.920 1.476 2.015 2.571 3.365 4.032 5.893 6.869
6 0.265 0.553 0.906 1.440 1.943 2.447 3.143 3.707 5.208 5.959
7 0.263 0.549 0.896 1.415 1.895 2.365 2.998 3.499 4.785 5.408
8 0.262 0.546 0.889 1.397 1.860 2.306 2.896 3.355 4.501 5.041
9 0.261 0.543 0.883 1.383 1.833 2.262 2.821 3.250 4.297 4.781
10 0.260 0.542 0.879 1.372 1.812 2.228 2.764 3.169 4.144 4.587
15 0.258 0.536 0.866 1.341 1.753 2.131 2.602 2.947 3.733 4.073
20 0.257 0.533 0.860 1.325 1.725 2.086 2.528 2.845 3.552 3.850
25 0.256 0.531 0.856 1.316 1.708 2.060 2.485 2.787 3.450 3.725
30 0.256 0.530 0.854 1.310 1.697 2.042 2.457 2.750 3.385 3.646
∞ 0.253 0.524 0.842 1.282 1.645 1.960 2.326 2.576 3.090 3.291
5