Abitur 2015; Aufgabe A 2.1

© www.mathe-abi-bw.de Mathe-Abi
Baden-Württemberg
Abitur 2015, Aufgabe A 2.1
Die Entwicklung einer Population in den Jahren 1960 bis 2020 lässt sich durch zwei
Funktionen modellhaft beschreiben. Die Funktion g mit g(t) = 400 + 20 ∙ (t + 1) 2 ∙ e −0,1t
beschreibt die Geburtenrate und die Funktion s mit s(t) = 600 + 10 ∙ (t − 6) 2 ∙ e −0,09t
beschreibt die Sterberate der Population (t in Jahren seit Beginn des Jahres 1960, g(t)
und s(t) in Individuen pro Jahr).
a) Bestimmen Sie die geringste Sterberate. In welchem Jahr war die Differenz aus
Geburten- und Sterberate am größten? Bestimmen Sie den Zeitraum, in dem die
Population zugenommen hat.
(4 VP)
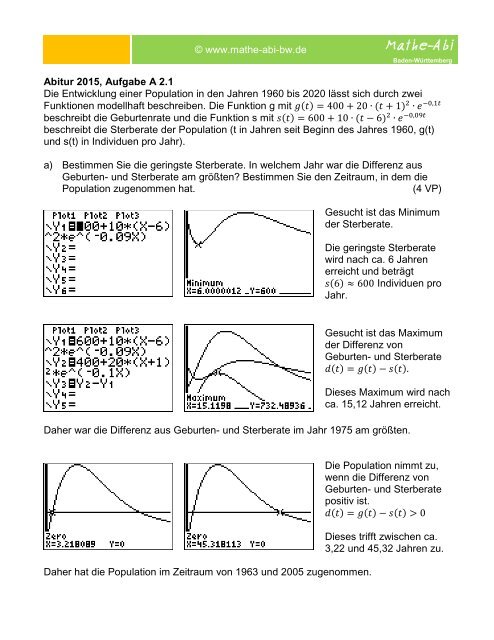
Gesucht ist das Minimum
der Sterberate.
Die geringste Sterberate
wird nach ca. 6 Jahren
erreicht und beträgt
s(6) ≈ 600 Individuen pro
Jahr.
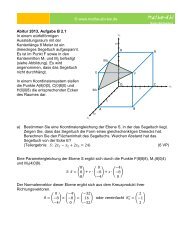
Gesucht ist das Maximum
der Differenz von
Geburten- und Sterberate
d(t) = g(t) − s(t).
Dieses Maximum wird nach
ca. 15,12 Jahren erreicht.
Daher war die Differenz aus Geburten- und Sterberate im Jahr 1975 am größten.
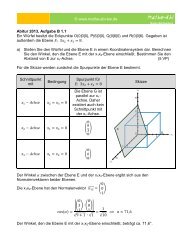
Daher hat die Population im Zeitraum von 1963 und 2005 zugenommen.
Die Population nimmt zu,
wenn die Differenz von
Geburten- und Sterberate
positiv ist.
d(t) = g(t) − s(t) > 0
Dieses trifft zwischen ca.
3,22 und 45,32 Jahren zu.

© www.mathe-abi-bw.de Mathe-Abi
Baden-Württemberg
b) Zu Beginn des Jahres 1960 bestand die Population aus 20.000 Individuen.
Berechnen Sie den Bestand der Population zu Beginn des Jahres 2017. In welchem
Jahr erreichte die Population erstmals wieder den Bestand von 1960? (3 VP)
Der Bestand wird mit einer Integralfunktion berechnet.
B(T = 57) = 20000 + ∫
0
57
g(t) − s(t) dt ≈ 35636
Zu Beginn des Jahres 2017 ergibt sich ein Bestand von
35.636 Individuen.
Damit die Population wieder den Bestand von 1960
erreicht, muss die Differenz der Geburten- und Sterbefälle
gleich Null sein.
T
B(T) = ∫ g(t) − s(t) dt = 0
0
Dieses trifft nach ca. 6,87 Jahren zu. Daher wird im Jahr
1966 erstmals wieder der Bestand von 1960 erreicht.

© www.mathe-abi-bw.de Mathe-Abi
Baden-Württemberg
Betrachtet wird nun das Größenwachstum eines einzelnen Individuums der Population.
Dies kann im Beobachtungszeitraum durch das Gesetz des beschränkten Wachstums
modelliert werden. Man geht davon aus, dass dieses Individuum in ausgewachsenem
Zustand 0,8m groß ist. Zu Beobachtungsbeginn betragen seine Größe 0,5m und seine
momentane Wachstumsgeschwindigkeit 0,15m pro Jahr.
c) Bestimmen Sie eine Gleichung einer Funktion, die die Körpergröße des Individuums
in Abhängigkeit von der Zeit beschreibt. Wie viele Jahre nach Beobachtungsbeginn
hat die Körpergröße des Individuums um 50% zugenommen?
(4 VP)
Beim beschränkten Wachstum ist die Wachstumsrate proportional zur Differenz aus einer
Schranke (auch Sättigungswert genannt) und dem aktuellen Bestand.
Die Differenzialgleichung lautet g′(t) = k ∙ (S − g(t))
Die Lösung dieser Differenzialgleichung lautet g(t) = S + (g(0) − S) ∙ e −kt
mit g(0) = 0,5; g´(0) = 0,15; S = 0,8 ⟹ k = g′ (0)
S−g(0) = 0,15
0,8−0,5 = 0,5
Die Gleichung der Funktion, die die Körpergröße des Individuums in Abhängigkeit von
der Zeit beschreibt lautet daher
g(t) = S + (g(0) − S) ∙ e −kt = 0,8 + (0,5 − 0,8) ∙ e −0,5t = 0,8 − 0,3 ∙ e −0,5t
Nachdem die Körpergröße des Individuums um 50% zugenommen hat, beträgt sie
g = 1,5 ∙ 0,5m = 0,75m
Für diesen Zeitpunkt gilt g(t) = S + (g(0) − S) ∙ e −kt = 0,8 − 0,3 ∙ e −0,5t = 0,75
Nach ca. 3,6 Jahren hat die Körpergröße des
Individuums um 50% zugenommen.