Section 4 - Pairs of Angles: - Willets Geometry
Section 4 - Pairs of Angles: - Willets Geometry
Section 4 - Pairs of Angles: - Willets Geometry
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
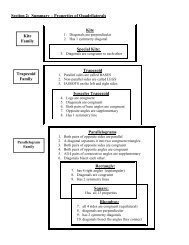
<strong>Section</strong> 4 - <strong>Pairs</strong> <strong>of</strong> <strong>Angles</strong>:<br />
1. ADJACENT ANGLES are two<br />
angles that have a common vertex<br />
and a common side between them.<br />
We can think <strong>of</strong> them as angles<br />
that are next to each other.<br />
2. If the sum <strong>of</strong> two angles is 90°,<br />
then the two angles are said to be<br />
COMPLEMENTARY.<br />
Each angle is the COMPLEMENT<br />
<strong>of</strong> the other<br />
3. If the sum <strong>of</strong> two angles is 180°,<br />
then the two angles are said<br />
to be SUPPLEMENTARY<br />
Each angle is the SUPPLEMENT<br />
<strong>of</strong> the other<br />
4. If AB and AC are opposite rays and<br />
AD is any third ray, then<br />
BAD and DAC<br />
are said to be a LINEAR PAIR.<br />
B C<br />
A<br />
42<br />
A<br />
P<br />
D<br />
35°<br />
ABD and DBC are<br />
adjacent angles.<br />
They both have vertex B and<br />
BD is between the other two<br />
rays.<br />
Q<br />
55°<br />
Since mP mQ 90<br />
, then the angles are<br />
complementary<br />
35°<br />
145°<br />
Since mA mB 180 , then the angles are<br />
supplementary<br />
B<br />
D<br />
B A C<br />
AB and AC are opposite rays.<br />
BADand DAC are a linear pair
5. If two angles form a linear pair, then they are supplementary.<br />
6. If two angles are complementary, then both must be acute angles.<br />
7. If two angles are congruent and complementary, then each angle contains 45°.<br />
8. If two angles are congruent and supplementary, then each angle contains 90°<br />
x x<br />
9. The angle formed by the bisectors <strong>of</strong> two<br />
complementary adjacent angles contains 45°<br />
AE bisects CAD and AF bisects DAB<br />
mEAF 45<br />
10. The angle formed by the bisectors <strong>of</strong> two<br />
supplementary adjacent angles contains 90°<br />
AE bisects CAD and AF bisects DAB<br />
mEAF 90<br />
BADand DAC are supplementary<br />
x x<br />
x x 180<br />
2x 180 11. The difference between the supplement and the<br />
complement <strong>of</strong> an angle is always 90°<br />
Angle Supplement Complement Supplement - Complement<br />
40 140 50 140 50 90<br />
23 157 67 157 67 90<br />
66 114 24 114 24 90<br />
81 99 9 99 9 90<br />
43<br />
x 90 x x 90<br />
C<br />
2x 90 x 45<br />
A<br />
C<br />
E<br />
E<br />
B<br />
A<br />
D<br />
F<br />
B<br />
D<br />
A<br />
F<br />
B<br />
D<br />
C
12. The non-adjacent angles formed when two straight lines intersect are called<br />
VERTICAL ANGLES.<br />
1<br />
4<br />
2<br />
3<br />
m<br />
13. VERTICAL ANGLE THEOREM: If two angles<br />
are vertical angles, then they are congruent<br />
to each other.<br />
n<br />
1 3 and 2 4<br />
When m and n intersect, four angles are formed.<br />
1and 3 are one pair <strong>of</strong> vertical angles<br />
2and 4 are another pair <strong>of</strong> vertical angles<br />
44<br />
1<br />
4<br />
2<br />
3<br />
m<br />
n
Assignment: <strong>Section</strong> 4<br />
1. The sum <strong>of</strong> two complementary angles is ____ degrees.<br />
2. The sum <strong>of</strong> two supplementary angles is ____ degrees.<br />
3. Which <strong>of</strong> the following pairs <strong>of</strong> angles are complementary?<br />
(a) 20° and 70° (b) 65° and 35° (c) 70° and 110°<br />
4. Which <strong>of</strong> the following pairs <strong>of</strong> angles are supplementary?<br />
(a) 30° and 60° (b) 140° and 50° (c) 70° and 110°<br />
5. The sum <strong>of</strong> an angle and its supplement is ____ degrees.<br />
6. The sum <strong>of</strong> an angle and its complement is ____ degrees.<br />
7. Find the complement <strong>of</strong> each angle<br />
(a) 33° (b) 52° (c) 15° (d) 2° (e) 82°<br />
8. Find the supplement <strong>of</strong> each angle<br />
(a) 33° (b) 52° (c) 15° (d) 2° (e) 82°<br />
9. The complement <strong>of</strong> an acute angle is always (a) acute (b) obtuse (c) right<br />
10. The supplement <strong>of</strong> a right angle is always (a) acute (b) obtuse (c) right<br />
11. The supplement <strong>of</strong> an acute angle is always (a) acute (b) obtuse (c) right<br />
12. The supplement <strong>of</strong> an obtuse angle is always (a) acute (b) obtuse (c) right<br />
13. If two angles are adjacent angles, then they must have a common _________ and a<br />
common ________ between them.<br />
14. (a) AEB and CED are called<br />
B<br />
E<br />
C (1) complementary angles (2) supplementary angles<br />
(3) adjacent angles (4) vertical angles<br />
A<br />
D<br />
(b) AEB and BEC are called<br />
(1) complementary angles (2) acute angles<br />
(3) a linear pair (4) vertical angles<br />
15. If two straight lines intersect, the vertical angles formed are always __________.<br />
16. The supplement <strong>of</strong> an angle <strong>of</strong> 40° contains (a) 40° (b) 50° (c) 140°<br />
17. If two congruent angles are supplementary, then each angle contains<br />
(a) 45° (b) 90° (c) 180°<br />
18. The difference between the supplement and the complement <strong>of</strong> an angle is<br />
(a) 45° (b) 90° (c) 180°<br />
45
19. In the diagram, m1 67 and m2 23<br />
Consider the following statements:<br />
Which <strong>of</strong> the three statements above are always true?<br />
(a) i and ii only (b) i and iii only (c) i, ii, and iii<br />
20. If two angles are a linear pair, then they must be<br />
(a) congruent (b) complementary (c) supplementary<br />
21. If an acute angle decreases, then its supplement<br />
(a) increases (b) decreases (c)remains the same<br />
22. If two straight lines intersect, the vertical angles formed are always<br />
(a) complementary (b) supplementary (c) congruent<br />
23. The difference between the supplement and the complement <strong>of</strong> an angle is<br />
(a) less than 90° (b) greater than 90° (c) 90°<br />
24. The supplement <strong>of</strong> an acute angle is always a(an) ____________ angle.<br />
25. The supplement <strong>of</strong> an obtuse angle is always a(an) _____________ angle.<br />
26. The supplement <strong>of</strong> a right angle is always a(an) ___________ angle.<br />
27. The complement <strong>of</strong> an acute angle is always a(an) ____________ angle.<br />
28. If two angles are congruent and complementary, then each angle contains _______<br />
degrees.<br />
29. The bisectors <strong>of</strong> two complementary adjacent angles form an angle <strong>of</strong> ___ degrees.<br />
30. The bisectors <strong>of</strong> two supplementary adjacent angles form an angle <strong>of</strong> ______<br />
degrees.<br />
31. If an angle is congruent to its supplement, then each angle contains _______ degrees.<br />
32. If two straight lines intersect, the _____________ angles formed are congruent.<br />
33. If two angles are complementary, then both must be<br />
(a) acute angles (b) obtuse angles (c) right angles<br />
34. If two angles form a linear pair, then they must be ___________________.<br />
35. Which <strong>of</strong> the following statements about AEB and BEC is NOT true?<br />
B<br />
E<br />
C<br />
A D<br />
i) 1and2areacute ii) 1and2arecomplementary iii) 1and2areadjacent (a) AEBandBECareadjacent angles<br />
(b) AEBandBECarealinear pair<br />
(c) AEBandBECaresupplementary (d) AEBandBECarevertical angles<br />
46<br />
A<br />
1<br />
2<br />
D<br />
B<br />
C