Section 9 - The Square and the Equilateral Triangle - Willets Geometry
Section 9 - The Square and the Equilateral Triangle - Willets Geometry
Section 9 - The Square and the Equilateral Triangle - Willets Geometry
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
<strong>Section</strong> 9 - <strong>The</strong> <strong>Square</strong> <strong>and</strong> <strong>the</strong> <strong>Equilateral</strong> <strong>Triangle</strong>:<br />
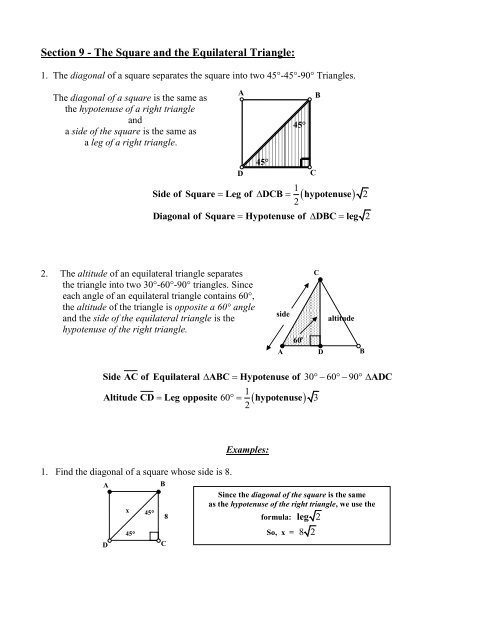
1. <strong>The</strong> diagonal of a square separates <strong>the</strong> square into two 45°-45°-90° <strong>Triangle</strong>s.<br />
<strong>The</strong> diagonal of a square is <strong>the</strong> same as<br />
<strong>the</strong> hypotenuse of a right triangle<br />
<strong>and</strong><br />
a side of <strong>the</strong> square is <strong>the</strong> same as<br />
a leg of a right triangle.<br />
1<br />
Side of <strong>Square</strong> Leg of DCB hypotenuse<br />
2<br />
<br />
Diagonal of <strong>Square</strong> Hypotenuse of DBC leg<br />
2. <strong>The</strong> altitude of an equilateral triangle separates<br />
<strong>the</strong> triangle into two 30°-60°-90° triangles. Since<br />
each angle of an equilateral triangle contains 60°,<br />
<strong>the</strong> altitude of <strong>the</strong> triangle is opposite a 60° angle<br />
<strong>and</strong> <strong>the</strong> side of <strong>the</strong> equilateral triangle is <strong>the</strong><br />
hypotenuse of <strong>the</strong> right triangle.<br />
Side AC of <strong>Equilateral</strong> ABC Hypotenuse of 30 60 90<br />
ADC<br />
1<br />
Altitude CD Leg opposite 60 hypotenuse 3<br />
2<br />
1. Find <strong>the</strong> diagonal of a square whose side is 8.<br />
A<br />
D<br />
x 45 <br />
45 <br />
B<br />
8<br />
C<br />
A B<br />
D<br />
45°<br />
Examples:<br />
side<br />
A<br />
45°<br />
60 <br />
Since <strong>the</strong> diagonal of <strong>the</strong> square is <strong>the</strong> same<br />
as <strong>the</strong> hypotenuse of <strong>the</strong> right triangle, we use <strong>the</strong><br />
formula: leg 2<br />
C<br />
So, x = 8 2<br />
C<br />
D<br />
altitude<br />
B<br />
2<br />
2
2. Find <strong>the</strong> side of a square whose diagonal is 12.<br />
3. Find <strong>the</strong> altitude of an equilateral triangle whose side is 12.<br />
A<br />
12<br />
60 <br />
A<br />
D<br />
C<br />
30 <br />
12<br />
45 <br />
x<br />
45 <br />
D B<br />
B<br />
C<br />
x<br />
Since <strong>the</strong> side of <strong>the</strong> square is <strong>the</strong> same as <strong>the</strong> leg of <strong>the</strong><br />
right triangle, we use <strong>the</strong> formula:<br />
1<br />
2 hypotenuse<br />
<br />
So, x = 6 2<br />
Since ABC is an equilateral triangle, mA60 .<br />
AC , <strong>the</strong> left side of <strong>the</strong> equilateral triangle<br />
is also <strong>the</strong> hypotenuse of ADC .<br />
In this triangle, “x” is <strong>the</strong> leg opposite <strong>the</strong> 60 angle.<br />
We use <strong>the</strong> formula: <br />
So, x = 6 3<br />
2<br />
1<br />
2 hypotenuse<br />
3
Assignment: <strong>Section</strong> 9<br />
1. Find <strong>the</strong> diagonal of a square whose side is 10.<br />
2. Find <strong>the</strong> side of a square whose diagonal is 16.<br />
3. Find <strong>the</strong> altitude of an equilateral triangle whose side is 6<br />
4. Find <strong>the</strong> side of a square whose diagonal is 12.<br />
5. Find <strong>the</strong> diagonal of a square whose side is 7.<br />
6. Find <strong>the</strong> altitude of an equilateral triangle whose side is 18.<br />
7. Find <strong>the</strong> diagonal of a square whose side is 14.<br />
8. Find <strong>the</strong> altitude of an equilateral triangle whose side is 16.<br />
9. Find <strong>the</strong> side of a square whose diagonal is 8.<br />
10. Find <strong>the</strong> altitude of an equilateral triangle whose side is 4.<br />
11. Find <strong>the</strong> diagonal of a square whose side is 3.<br />
12. Find <strong>the</strong> side of a square whose diagonal is 14.