Section 1: Types of Quadrilaterals The Trapezoid ... - Willets Geometry
Section 1: Types of Quadrilaterals The Trapezoid ... - Willets Geometry
Section 1: Types of Quadrilaterals The Trapezoid ... - Willets Geometry
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
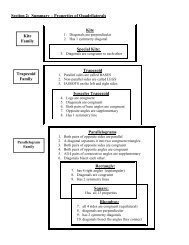
<strong>Section</strong> 1: <strong>Types</strong> <strong>of</strong> <strong>Quadrilaterals</strong><br />
A quadrilateral is a figure with four sides. It is named<br />
by naming its vertices in a clockwise or counter-clockwise<br />
direction. Although there are many types <strong>of</strong> quadrilaterals,<br />
we will concentrate on three families <strong>of</strong> quadrilaterals:<br />
<strong>Trapezoid</strong><br />
Kite<br />
Parallelogram<br />
<strong>The</strong> <strong>Trapezoid</strong> Family: <strong>Trapezoid</strong> and Isosceles <strong>Trapezoid</strong><br />
(a) A TRAPEZOID is a quadrilateral with two and only two sides parallel.<br />
<strong>The</strong> parallel sides are called the BASES<br />
<strong>The</strong> non-parallel sides are called the LEGS.<br />
IASSOTS on the left and right sides are<br />
supplementary so<br />
(b) A trapezoid whose legs are congruent is called an ISOSCELES TRAPEZOID.<br />
PT RQ<br />
AB DC but<br />
AD is not parallel to BC<br />
m1 m3 180 and<br />
m2 m4 180<br />
P<br />
T<br />
An isosceles trapezoid has all the properties <strong>of</strong> a trapezoid<br />
An isosceles trapezoid has a vertical<br />
symmetry line, which means that when<br />
folded from left to right, it coincides<br />
with itself.<br />
<strong>The</strong> base angles <strong>of</strong> an isosceles T<br />
trapezoid are congruent<br />
3<br />
1 2 and 3 4<br />
1<br />
Opposite angles <strong>of</strong> an isosceles<br />
trapezoid are supplementary<br />
P<br />
m1 m4 180 and m2 m3 180 In an isosceles trapezoid, the<br />
diagonals are congruent so PR TQ<br />
R<br />
Q<br />
D C<br />
A B<br />
D C<br />
1<br />
3<br />
A B<br />
P<br />
P<br />
4<br />
R<br />
1<br />
2<br />
T<br />
T<br />
3<br />
4<br />
Q<br />
2<br />
4<br />
R<br />
R<br />
2<br />
Q<br />
Q
<strong>The</strong> Kite Family: Kite and Special Kite<br />
(a) A KITE has two distinct pairs <strong>of</strong> congruent adjacent sides.<br />
AB BC and AD CD<br />
but AB is not congruent to AD<br />
and BC is not congruent to CD<br />
If diagonal AC is drawn, a kite can be thought <strong>of</strong> as two<br />
isosceles triangles that have a common base. <strong>The</strong> segment<br />
connecting the vertex angles <strong>of</strong> these isosceles triangles<br />
is called the SYMMETRY DIAGONAL. If the kite is folded<br />
left to right, it will coincide with itself.<br />
BD is the symmetry diagonal.<br />
<strong>The</strong> symmetry diagonal bisects the angles it connect.<br />
If you fold a kite along the symmetry diagonal, any angles that<br />
coincide will be congruent : 1 2 and 3 4<br />
In a kite, the diagonals are perpendicular:<br />
mAEB = mBEC = mDEC = mDEA = 90°<br />
<strong>The</strong> symmetry diagonal <strong>of</strong> a kite bisects the other diagonal.<br />
AE = EC but BE ≠ ED<br />
(b) A kite whose diagonals are congruent is<br />
called a SPECIAL KITE.<br />
FH GE<br />
A special kite has all the properties <strong>of</strong> a kite.<br />
B<br />
A C<br />
D<br />
B<br />
A C<br />
E<br />
G<br />
D<br />
F H<br />
E<br />
1 2<br />
A C<br />
3<br />
B<br />
D<br />
4
<strong>The</strong> Parallelogram Family: Parallelogram, Rectangle, Rhombus and Square<br />
(a) A PARALLELOGRAM is a quadrilateral<br />
with both pairs <strong>of</strong> opposite sides parallel.<br />
AB CD and AD BC<br />
A diagonal <strong>of</strong> a parallelogram, separates it<br />
into two congruent triangles.<br />
ADC CBA<br />
Both pairs <strong>of</strong> opposite sides are congruent<br />
AB DCandADBC Both pairs <strong>of</strong> opposite angles are congruent<br />
1 3 and 2 4<br />
All four pairs <strong>of</strong> consecutive angles are supplementary<br />
m1 m2 180 and m2 m3 180<br />
m3 m4 180 and m4 m1 180<br />
<strong>The</strong> diagonals <strong>of</strong> a parallelogram bisect each other<br />
M is the midpoint <strong>of</strong> AC and<br />
M is the midpoint <strong>of</strong> BD<br />
(b) A RECTANGLE is a parallelogram with 4 right angles.<br />
A rectangle is an equiangular quadrilateral.<br />
A rectangle has all the properties <strong>of</strong> a parallelogram.<br />
<strong>The</strong> diagonals <strong>of</strong> a rectangle are congruent: AC BD<br />
A rectangle has 2 symmetry lines. However, neither<br />
diagonal is a symmetry diagonal.<br />
D<br />
A B<br />
D<br />
A B<br />
1<br />
D<br />
4<br />
A B<br />
A D<br />
B<br />
D<br />
A<br />
2<br />
M<br />
3<br />
C<br />
A B<br />
D<br />
D<br />
C<br />
C<br />
C<br />
C<br />
B<br />
A B<br />
C<br />
C
(c) A RHOMBUS is a quadrilateral with all four sides congruent.<br />
A rhombus is an equilateral quadrilateral.<br />
AB BC DC <br />
AD<br />
A rhombus has all the properties <strong>of</strong> a parallelogram<br />
<strong>The</strong> diagonals <strong>of</strong> a rhombus are perpendicular.<br />
AC BD<br />
A rhombus has two symmetry diagonals<br />
A rhombus can be folded left to right and,<br />
unlike a kite, it can also be folded top to bottom.<br />
Any segments or angles that fold onto each other<br />
are congruent.<br />
<strong>The</strong> diagonals <strong>of</strong> a rhombus bisect the angles<br />
they connect.<br />
1 2, 3 4, 5 6 and 7 8<br />
(d) A SQUARE is a quadrilateral with 4 right angles and 4 congruent sides.<br />
A square is a regular quadrilateral since it is both equilateral<br />
and equiangular.<br />
A square has all the properties <strong>of</strong> a parallelogram,<br />
all the properties <strong>of</strong> a rectangle and all the properties <strong>of</strong> a rhombus.<br />
<strong>The</strong> diagonals <strong>of</strong> a square are perpendicular, congruent<br />
and bisect each other.<br />
AC BD, AC BD<br />
M is the midpoint <strong>of</strong> AC<br />
M is the midpoint <strong>of</strong> BD<br />
A square has 4 symmetry lines,<br />
two <strong>of</strong> which are symmetry diagonals.<br />
A<br />
A<br />
1<br />
D<br />
5<br />
7<br />
A C<br />
6<br />
8<br />
B<br />
A<br />
D<br />
3<br />
D<br />
B<br />
B<br />
M<br />
2<br />
4<br />
A<br />
B<br />
D<br />
C<br />
B<br />
C<br />
C<br />
D<br />
C