unit 1 differential calculus - IGNOU

Example 1.20
Solution
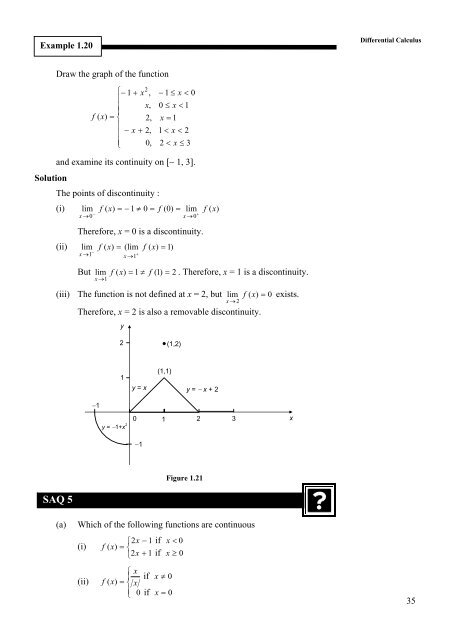
Draw the graph of the function
⎧ 2
− 1 + x ,
⎪
⎪ x,
⎪
f ( x)
= ⎨ 2,
⎪
⎪
− x + 2,
⎪⎩
0,
− 1 ≤ x < 0
0 ≤ x < 1
x = 1
1 < x < 2
2 < x ≤ 3
and examine its continuity on [− 1, 3].
The points of discontinuity :
(i) lim f ( x)
= − 1 ≠ 0 = f ( 0)
= lim f ( x)
(ii)
−
x →0
+
x →0
Therefore, x = 0 is a discontinuity.
lim
−
x →1
f ( x)
= (lim
+
x →1
f ( x)
= 1)
But f ( x)
= 1 ≠ f ( 1)
= 2 . Therefore, x = 1 is a discontinuity.
lim
x →1
(iii) The function is not defined at x = 2, but f ( x)
= 0 exists.
SAQ 5
lim
x →2
Therefore, x = 2 is also a removable discontinuity.
−1
y
2
1
y = −1+x 2
y = x
0
−1
(1,1)
1
(1,2)
y = − x + 2
Figure 1.21
2 3
(a) Which of the following functions are continuous
(i)
(ii)
⎧2x
− 1 if
f ( x)
= ⎨
⎩2x
+ 1 if
⎧ x
⎪ if
f
( x)
= ⎨|
x|
⎪
⎩ 0 if
x ≠ 0
x = 0
x < 0
x ≥ 0
x
Differential Calculus
35