Getting a Handle on Advanced Cubic Equations of State
Getting a Handle on Advanced Cubic Equations of State
Getting a Handle on Advanced Cubic Equations of State
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
Measurement & C<strong>on</strong>trol<br />
Unfortunately, the accuracy <strong>of</strong> predicting<br />
vapor pressure from Soave’s new α(T)<br />
was no better than the original <strong>on</strong>e, and<br />
c<strong>on</strong>sequently, was never accepted for applicati<strong>on</strong>.<br />
Numerous investigators have<br />
tried to improve Soave’s alpha functi<strong>on</strong><br />
by either altering the parameters or<br />
adding extra terms. But as l<strong>on</strong>g as the<br />
same or a similar form <strong>of</strong> the alpha functi<strong>on</strong><br />
is used, and the same approach as<br />
Soave is applied (i.e., plotting α 0.5 vs.<br />
T r 0.5), the functi<strong>on</strong>’s inherent weaknesswill<br />
not be overcome.<br />
Better vapor pressure predicti<strong>on</strong><br />
Twu et. al. (10, 11) developed a new<br />
methodology to improve the accuracy <strong>of</strong> the<br />
vapor-pressure predicti<strong>on</strong> from a CEOS.<br />
They found that the alpha functi<strong>on</strong> is a linear<br />
functi<strong>on</strong> <strong>of</strong> the acentric factor at a c<strong>on</strong>stant<br />
reduced temperature.<br />
α = α (0) + ω(α (1) – α (0) ) (10)<br />
α ( ) ( ) 0 N M − 1 L ( 1−<br />
T )<br />
=<br />
e r<br />
T r<br />
( 1) ( 1)<br />
N M<br />
α () ( ) ( 1) ( 1) ( 1)<br />
1 N M − 1 L ( 1−<br />
T )<br />
=<br />
e r<br />
T r<br />
( 0) ( 0) ( 0 )<br />
( 0 ) ( 0 )<br />
N M<br />
( 11)<br />
( 12)<br />
The superscripts (0) and (1) in Eqs. 10, 11 and 12 are c<strong>on</strong>sistent<br />
with the definiti<strong>on</strong> <strong>of</strong> the acentric factor at ω = 0 and ω<br />
=1, respectively. In other words, these two alpha functi<strong>on</strong>s are<br />
forced to pass through the saturated vapor pressure at T r = 0.7<br />
for ω = 0 and ω = 1, respectively.<br />
Twu et. al. used the latest data from the DIPPR (12) databank<br />
to generate the values <strong>of</strong> α (0) and α (1) for SRK, PR and<br />
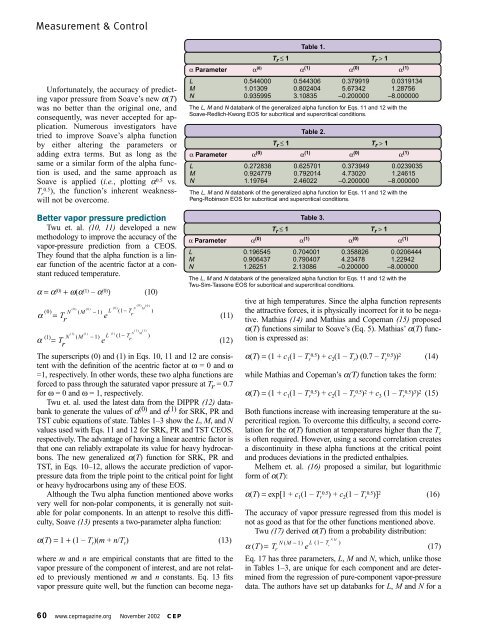
TST cubic equati<strong>on</strong>s <strong>of</strong> state. Tables 1–3 show the L, M, and N<br />
values used with Eqs. 11 and 12 for SRK, PR and TST CEOS,<br />
respectively. The advantage <strong>of</strong> having a linear acentric factor is<br />
that <strong>on</strong>e can reliably extrapolate its value for heavy hydrocarb<strong>on</strong>s.<br />
The new generalized α(T) functi<strong>on</strong> for SRK, PR and<br />
TST, in Eqs. 10–12, allows the accurate predicti<strong>on</strong> <strong>of</strong> vaporpressure<br />
data from the triple point to the critical point for light<br />
or heavy hydrocarb<strong>on</strong>s using any <strong>of</strong> these EOS.<br />
Although the Twu alpha functi<strong>on</strong> menti<strong>on</strong>ed above works<br />
very well for n<strong>on</strong>-polar comp<strong>on</strong>ents, it is generally not suitable<br />
for polar comp<strong>on</strong>ents. In an attenpt to resolve this difficulty,<br />
Soave (13) presents a two-parameter alpha functi<strong>on</strong>:<br />
α(T) = 1 + (1 – T r )(m + n/T r ) (13)<br />
where m and n are empirical c<strong>on</strong>stants that are fitted to the<br />
vapor pressure <strong>of</strong> the comp<strong>on</strong>ent <strong>of</strong> interest, and are not related<br />
to previously menti<strong>on</strong>ed m and n c<strong>on</strong>stants. Eq. 13 fits<br />
vapor pressure quite well, but the functi<strong>on</strong> can become nega-<br />
60 www.cepmagazine.org November 2002 CEP<br />
Table 1.<br />
Tr ≤ 1 Tr > 1<br />
α Parameter α (0) α (1) α (0) α (1)<br />
L 0.544000 0.544306 0.379919 0.0319134<br />
M 1.01309 0.802404 5.67342 1.28756<br />
N 0.935995 3.10835 –0.200000 –8.000000<br />
The L, M and N databank <strong>of</strong> the generalized alpha functi<strong>on</strong> for Eqs. 11 and 12 with the<br />
Soave-Redlich-Kw<strong>on</strong>g EOS for subcritical and supercritical c<strong>on</strong>diti<strong>on</strong>s.<br />
Table 2.<br />
Tr ≤ 1 Tr > 1<br />
α Parameter α (0) α (1) α (0) α (1)<br />
L 0.272838 0.625701 0.373949 0.0239035<br />
M 0.924779 0.792014 4.73020 1.24615<br />
N 1.19764 2.46022 –0.200000 –8.000000<br />
The L, M and N databank <strong>of</strong> the generalized alpha functi<strong>on</strong> for Eqs. 11 and 12 with the<br />
Peng-Robins<strong>on</strong> EOS for subcritical and supercritical c<strong>on</strong>diti<strong>on</strong>s.<br />
Table 3.<br />
Tr ≤ 1 Tr > 1<br />
α Parameter α (0) α (1) α (0) α (1)<br />
L 0.196545 0.704001 0.358826 0.0206444<br />
M 0.906437 0.790407 4.23478 1.22942<br />
N 1.26251 2.13086 –0.200000 –8.000000<br />
The L, M and N databank <strong>of</strong> the generalized alpha functi<strong>on</strong> for Eqs. 11 and 12 with the<br />
Twu-Sim-Tass<strong>on</strong>e EOS for subcritical and supercritical c<strong>on</strong>diti<strong>on</strong>s.<br />
tive at high temperatures. Since the alpha functi<strong>on</strong> represents<br />
the attractive forces, it is physically incorrect for it to be negative.<br />
Mathias (14) and Mathias and Copeman (15) proposed<br />
α(T) functi<strong>on</strong>s similar to Soave’s (Eq. 5). Mathias’ α(T) functi<strong>on</strong><br />
is expressed as:<br />
α(T) = (1 + c 1 (1 – T r 0.5) + c 2 (1 – T r ) (0.7 – T r 0.5)) 2 (14)<br />
while Mathias and Copeman’s α(Τ) functi<strong>on</strong> takes the form:<br />
α(T) = (1 + c 1 (1 – T r 0.5) + c 2 (1 – T r 0.5) 2 + c 3 (1 – T r 0.5) 3 ) 2 (15)<br />
Both functi<strong>on</strong>s increase with increasing temperature at the supercritical<br />
regi<strong>on</strong>. To overcome this difficulty, a sec<strong>on</strong>d correlati<strong>on</strong><br />
for the α(T) functi<strong>on</strong> at temperatures higher than the T c<br />
is <strong>of</strong>ten required. However, using a sec<strong>on</strong>d correlati<strong>on</strong> creates<br />
a disc<strong>on</strong>tinuity in these alpha functi<strong>on</strong>s at the critical point<br />
and produces deviati<strong>on</strong>s in the predicted enthalpies.<br />
Melhem et. al. (16) proposed a similar, but logarithmic<br />
form <strong>of</strong> α(T):<br />
α(T) = exp[1 + c 1 (1 – T r 0.5) + c 2 (1 – T r 0.5)] 2 (16)<br />
The accuracy <strong>of</strong> vapor pressure regressed from this model is<br />
not as good as that for the other functi<strong>on</strong>s menti<strong>on</strong>ed above.<br />
Twu (17) derived α(T) from a probability distributi<strong>on</strong>:<br />
NM<br />
N( M − 1) L ( 1−<br />
T ) r<br />
r<br />
α ( T) = T e<br />
( 17)<br />
Eq. 17 has three parameters, L, M and N, which, unlike those<br />
in Tables 1–3, are unique for each comp<strong>on</strong>ent and are determined<br />
from the regressi<strong>on</strong> <strong>of</strong> pure-comp<strong>on</strong>ent vapor-pressure<br />
data. The authors have set up databanks for L, M and N for a