Introduction to String Theory and D–Branes - School of Natural ...
Introduction to String Theory and D–Branes - School of Natural ...
Introduction to String Theory and D–Branes - School of Natural ...
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
= α′ k2 1<br />
4 (z − y) 2 : eik·X(y) ik · ∂zX(z)<br />
: + : e<br />
(z − y)<br />
ik·X(y) :<br />
= α′ k 2<br />
4<br />
V (y)<br />
(z − y) 2 + ∂yV (y)<br />
(z − y)<br />
, (158)<br />
We have Taylor exp<strong>and</strong>ed in the last line, <strong>and</strong> throughout we only displayed explicitly the singular parts.<br />
The expressions tidy up themselves quite nicely if one realizes that the worst singularity comes from when<br />
there are two contractions with products <strong>of</strong> fields using up both pieces <strong>of</strong> T(z). Everything else is either non–<br />
singular, or sums <strong>to</strong> reassemble the exponential after combina<strong>to</strong>rial fac<strong>to</strong>rs have been taken in<strong>to</strong> account.<br />
This gives the first term <strong>of</strong> the second line. The second term <strong>of</strong> that line comes from single contractions.<br />
The fac<strong>to</strong>r <strong>of</strong> two comes from making two choices <strong>to</strong> contract with one or other <strong>of</strong> the two identical pieces <strong>of</strong><br />
T(z), while there are other fac<strong>to</strong>rs coming from the n ways <strong>of</strong> choosing a field from the term <strong>of</strong> order n from<br />
the expansion <strong>of</strong> the exponential. After dropping the non–singular term, the remaining terms (with the n)<br />
reassemble the exponential again. (The reader is advised <strong>to</strong> check this explicitly <strong>to</strong> see how it works.) The<br />
final result (when combined with the anti–holomorphic counterpart) shows that V (y) is a primary field <strong>of</strong><br />
weight (α ′ k 2 /4, α ′ k 2 /4).<br />
Now we can pause <strong>to</strong> see what this all means. Recall from section 2.9.2 that the insertion <strong>of</strong> states is<br />
equivalent <strong>to</strong> the insertion <strong>of</strong> opera<strong>to</strong>rs in<strong>to</strong> the theory, so that:<br />
S → S ′ <br />
= S + λ d 2 zO(z, ¯z) . (159)<br />
In general, we may consider such an opera<strong>to</strong>r insertion for a general theory. For the theory <strong>to</strong> remain<br />
conformally invariant, the opera<strong>to</strong>r must be a marginal opera<strong>to</strong>r, which is <strong>to</strong> say that O(z, ¯z) must at least<br />
have dimension (1, 1) so that the integrated opera<strong>to</strong>r is dimensionless. In principle, the dimension <strong>of</strong> the<br />
opera<strong>to</strong>r after the deformation (i.e. in the new theory defined by S ′ ) can change, <strong>and</strong> so the full condition<br />
for the opera<strong>to</strong>r is that it must remain (1, 1) after the insertion. It in fact defines a direction in the space<br />
<strong>of</strong> couplings, <strong>and</strong> λ can be thought <strong>of</strong> as an infinitessimal motion in that direction. The statement <strong>of</strong> the<br />
existence <strong>of</strong> a marginal opera<strong>to</strong>r is then referred <strong>to</strong> the existence <strong>of</strong> a “flat direction”.<br />
A useful picture <strong>to</strong> have in mind for later use is <strong>of</strong> a conformal field theory as a “fixed point” in the space<br />
<strong>of</strong> theories with coordinates given by the coefficients <strong>of</strong> possible opera<strong>to</strong>rs such as in equation (159). (There<br />
is an infinite set <strong>of</strong> such perturbations <strong>and</strong> so the space is infinite dimensional.) In the usual reasoning using<br />
the renomalisation group (RG), once the opera<strong>to</strong>r is added with some value <strong>of</strong> the coupling, the theory (i.e.<br />
the value <strong>of</strong> the coupling) flows along an RG trajec<strong>to</strong>ry as the energy scale µ is changed. The “β–function”,<br />
β(λ) ≡ µ∂λ/∂µ characterizes the behaviour <strong>of</strong> the coupling. One can imagine the existence <strong>of</strong> “fixed points”<br />
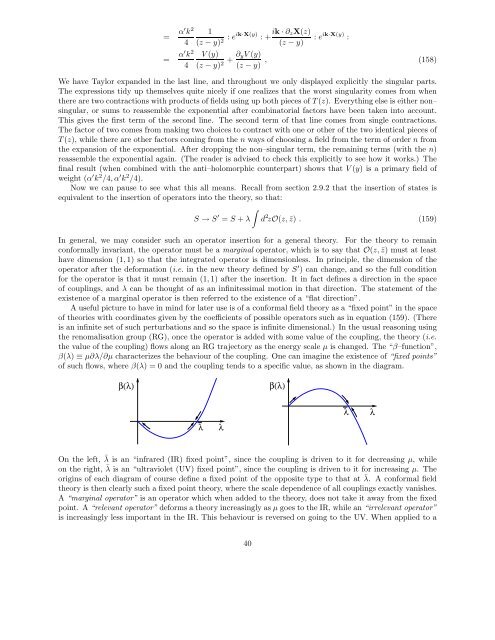
<strong>of</strong> such flows, where β(λ) = 0 <strong>and</strong> the coupling tends <strong>to</strong> a specific value, as shown in the diagram.<br />
β(λ)<br />
λ<br />
λ<br />
On the left, ¯ λ is an “infrared (IR) fixed point”, since the coupling is driven <strong>to</strong> it for decreasing µ, while<br />
on the right, ¯ λ is an “ultraviolet (UV) fixed point”, since the coupling is driven <strong>to</strong> it for increasing µ. The<br />
origins <strong>of</strong> each diagram <strong>of</strong> course define a fixed point <strong>of</strong> the opposite type <strong>to</strong> that at ¯ λ. A conformal field<br />
theory is then clearly such a fixed point theory, where the scale dependence <strong>of</strong> all couplings exactly vanishes.<br />
A “marginal opera<strong>to</strong>r” is an opera<strong>to</strong>r which when added <strong>to</strong> the theory, does not take it away from the fixed<br />
point. A “relevant opera<strong>to</strong>r” deforms a theory increasingly as µ goes <strong>to</strong> the IR, while an “irrelevant opera<strong>to</strong>r”<br />
is increasingly less important in the IR. This behaviour is reversed on going <strong>to</strong> the UV. When applied <strong>to</strong> a<br />
40<br />
β(λ)<br />
λ<br />
λ