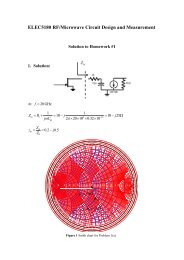
Ch3.3: Fast Fourier Transform
Ch3.3: Fast Fourier Transform
Ch3.3: Fast Fourier Transform
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
<strong>Ch3.3</strong>: <strong>Fast</strong> <strong>Fourier</strong> <strong>Transform</strong><br />
Information source<br />
and input transducer<br />
Source Coding<br />
Channel Coding<br />
Modulator<br />
<strong>Ch3.3</strong>: FFT<br />
• Questions to be answered:<br />
– <strong>Fast</strong>-<strong>Fourier</strong> <strong>Transform</strong>: How<br />
can we efficiently compute DFT.<br />
Channel<br />
Information sink<br />
and output transducer<br />
Source Decoding<br />
Channel Decoding<br />
Demodulator<br />
(Matched Filter)<br />
Elec3100 Chapter 3.3 1
FFT Applications<br />
‣ OFDM<br />
‣ DAB<br />
‣ HDTV<br />
‣ Wireless LAN Networks<br />
‣ 1 HIPERLAN/2<br />
‣ 2 IEEE 802.11a<br />
‣ 3 IEEE 802.11g<br />
‣ IEEE 802.16 Broadband Wireless Access Systems<br />
Elec3100 Chapter 3.3<br />
2
Computation Complexity of DFT<br />
Elec3100 Chapter 3.3<br />
3
Computation Complexity of DFT<br />
Elec3100 Chapter 3.3<br />
4
Efficient Computation of DFT<br />
Elec3100 Chapter 3.3<br />
5
Efficient Computation of DFT<br />
Elec3100 Chapter 3.3<br />
6
Decimation-in-Time FFT Algorithm<br />
Elec3100 Chapter 3.3<br />
7
Decimation-in-Time FFT Algorithm<br />
Elec3100 Chapter 3.3<br />
8
Decimation-in-Time FFT Algorithm<br />
• The N/2-point DFTs of the even- and odd-numbered sequences, G[k]<br />
and H[k], are calculated for the range k = 0…(N/2-1)<br />
• However, the values of the N/2-point DFT vary periodically with period<br />
N/2<br />
– G[k] = G[k + N/2] and H[k] = H[k + N/2]<br />
• Therefore, we can compute all points of the N-point DFT using two N/2-<br />
point DFTs as follows<br />
k<br />
N<br />
X[ k]<br />
= G[<br />
k]<br />
+ WN<br />
H[<br />
k]<br />
0 ≤ k ≤ −1<br />
2<br />
X<br />
k + N / 2<br />
[ k + N / 2] = G[ k] + W H[ k]<br />
= G k<br />
N<br />
N<br />
2<br />
k<br />
[ ] −W<br />
H[ k] 0 ≤ k ≤ −1<br />
N<br />
W<br />
N/ 2<br />
N<br />
=<br />
=<br />
e<br />
e<br />
-j( 2π/N)(N/<br />
2 )<br />
− jπ<br />
= -1<br />
Elec3100 Chapter 3.3<br />
9
Decimation-in-Time FFT Algorithm<br />
Fig. 1 Flow Graph Representation of N-Point DFT Computation Using Two N/2-Point DFTs<br />
Elec3100 Chapter 3.3<br />
10
Decimation-in-Time FFT Algorithm - Example<br />
Elec3100 Chapter 3.3<br />
11
Decimation-in-Time FFT Algorithm<br />
For large N, the computational load of the DIT-FFT is<br />
approximately halved !<br />
Elec3100 Chapter 3.3<br />
12
Decimation-in-Time FFT Algorithm - Example<br />
Construct each of the 4-point DFTs using a combination of 2-point DFTs<br />
Elec3100 Chapter 3.3<br />
13
Decimation-in-Time FFT Algorithm - Example<br />
Construct each of the 4-point DFTs using a combination of 2-point DFTs<br />
Elec3100 Chapter 3.3<br />
14
Decimation-in-Time FFT Algorithm - Example<br />
Construct each of the 2-point DFTs using an elementary butterfly<br />
Elec3100 Chapter 3.3<br />
15
Decimation-in-Time FFT Algorithm - Example<br />
Elec3100 Chapter 3.3<br />
16
Decimation-in-Time FFT Algorithm - Example<br />
Elec3100 Chapter 3.3<br />
2-Point DFTs<br />
Combination of<br />
2-Point DFTs<br />
Combination of<br />
4-Point DFTs<br />
17
Decimation-in-Time FFT Algorithm<br />
Elec3100 Chapter 3.3<br />
18
Decimation-in-Time FFT Algorithm<br />
Elec3100 Chapter 3.3<br />
19
Decimation-in-Time FFT Algorithm<br />
FFT can give orders of magnitude complexity savings<br />
compared with direct evaluation of DFT !!<br />
Elec3100 Chapter 3.3<br />
20